3 X 3 - 3 / 3 3
catholicpriest
Nov 26, 2025 · 13 min read
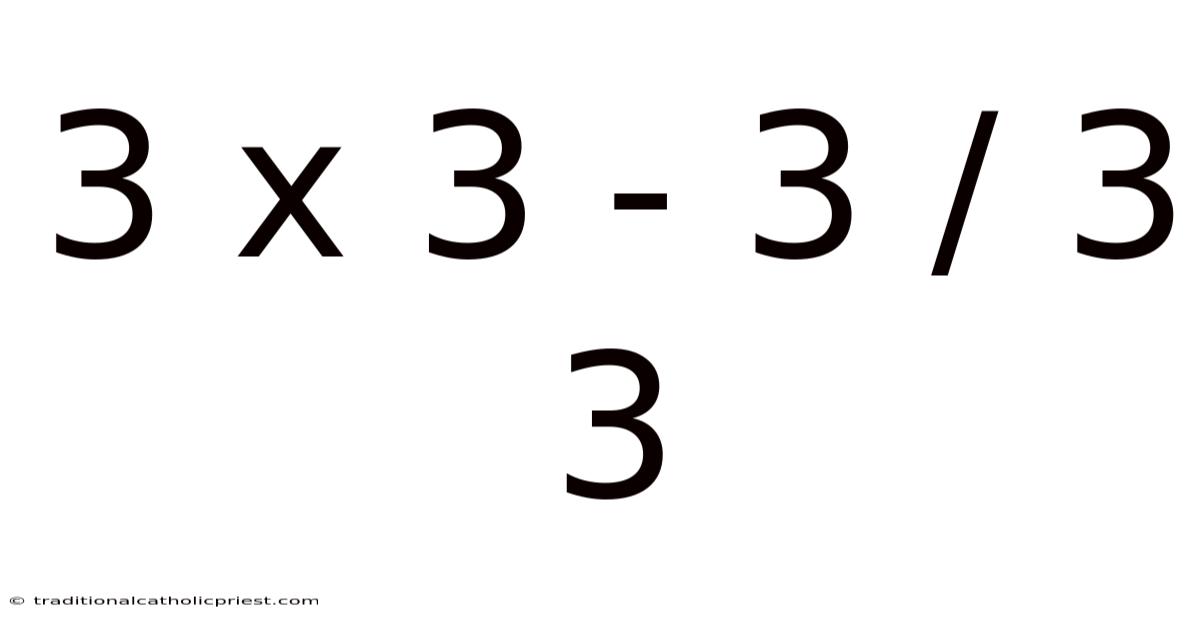
Table of Contents
Have you ever looked at a seemingly simple math problem and felt a wave of confusion wash over you? It happens to the best of us. Math, at its core, is a language, and like any language, it has its own set of rules and syntax. Understanding these rules is essential to unraveling complex equations and arriving at the correct answer.
One such equation that often sparks debate and confusion is 3 x 3 - 3 / 3 + 3. At first glance, it appears straightforward, but the order in which we perform the operations dramatically affects the outcome. This article will break down the intricacies of this problem, exploring the fundamental principles that govern mathematical operations and providing clarity on how to solve it correctly. We’ll explore the order of operations, delve into common pitfalls, and provide clear, step-by-step guidance to ensure you master this and similar math problems. Prepare to demystify this equation and enhance your problem-solving skills.
Unveiling the Order of Operations
The cornerstone of solving any mathematical expression is understanding the order of operations. This set of rules dictates the sequence in which calculations should be performed to ensure consistency and accuracy. Without it, the same equation could yield different results, leading to chaos and misunderstanding. The universally recognized mnemonic for the order of operations is PEMDAS, which stands for Parentheses, Exponents, Multiplication and Division (from left to right), and Addition and Subtraction (from left to right).
PEMDAS ensures that everyone, regardless of their location or background, arrives at the same answer when solving a mathematical problem. This standardized approach is crucial in fields like science, engineering, finance, and computer science, where precision and consistency are paramount. By adhering to PEMDAS, we eliminate ambiguity and promote clear communication through the universal language of mathematics.
Now, let’s delve deeper into each component of PEMDAS to understand its importance and application:
- Parentheses (or Brackets): These symbols
()indicate that the operations enclosed within them should be performed first. Parentheses can be nested, meaning one set of parentheses can contain another. In such cases, you start with the innermost set and work your way outwards. Parentheses are used to group terms and prioritize certain operations, ensuring they are executed before others. - Exponents: Exponents involve raising a number (the base) to a certain power. For example, in
2^3, 2 is the base and 3 is the exponent, meaning you multiply 2 by itself three times (2 x 2 x 2 = 8). Exponents signify repeated multiplication and are performed after any operations within parentheses. - Multiplication and Division: These operations are performed from left to right. It’s crucial to understand that multiplication and division have equal priority. Therefore, you execute them in the order they appear in the equation. For instance, if you have
10 / 2 x 3, you would first divide 10 by 2 (resulting in 5) and then multiply by 3 (resulting in 15). - Addition and Subtraction: Similar to multiplication and division, addition and subtraction are performed from left to right. They also have equal priority, so you execute them in the order they appear. For example, in
8 - 3 + 2, you would first subtract 3 from 8 (resulting in 5) and then add 2 (resulting in 7).
A Historical Perspective on the Order of Operations
The development of a standardized order of operations wasn't an overnight process; it evolved over centuries as mathematical notation became more sophisticated. Early mathematical texts often lacked clear conventions, leading to ambiguity and confusion. Mathematicians gradually recognized the need for a consistent set of rules to ensure clarity and accuracy.
The formalization of the order of operations can be traced back to the 19th and 20th centuries. Mathematicians like Giuseppe Peano and his followers played a crucial role in establishing a clear and unambiguous notation. The introduction of symbols like parentheses and exponents, along with the convention of performing multiplication and division before addition and subtraction, helped to eliminate much of the confusion that had plagued earlier mathematical writings.
The adoption of PEMDAS (or similar mnemonics like BODMAS or BIDMAS in other countries) further solidified the order of operations as a universal standard. These mnemonics provide a simple and memorable way to remember the correct sequence, making it easier for students and professionals alike to apply the rules consistently.
Why the Order of Operations Matters
The order of operations isn't just an arbitrary set of rules; it's a fundamental principle that underpins all of mathematics. Without it, mathematical expressions would be ambiguous, and calculations would be unreliable. Imagine trying to build a bridge or design a computer without a consistent set of rules for performing calculations – the results would be disastrous.
In fields like physics and engineering, the order of operations is essential for solving equations that describe the behavior of the physical world. In finance, it's used to calculate interest rates, investment returns, and other financial metrics. In computer science, it's used to write algorithms and programs that perform complex calculations.
Moreover, understanding the order of operations is crucial for developing critical thinking and problem-solving skills. It teaches you to approach problems systematically, break them down into smaller steps, and apply logical reasoning to arrive at the correct solution. These skills are valuable not only in mathematics but also in many other areas of life.
Common Pitfalls and How to Avoid Them
Even with a clear understanding of the order of operations, it's easy to make mistakes if you're not careful. Here are some common pitfalls to watch out for:
- Forgetting the Left-to-Right Rule: When performing multiplication and division (or addition and subtraction), remember to work from left to right. It's easy to get tripped up if you don't follow this rule consistently.
- Ignoring Parentheses: Always prioritize operations within parentheses. Make sure you've completely simplified the expression inside the parentheses before moving on to other operations.
- Misinterpreting Exponents: Double-check that you understand what the exponent means. For example,
2^3means 2 multiplied by itself three times, not 2 multiplied by 3. - Rushing Through the Problem: Take your time and work through each step carefully. Rushing can lead to careless errors, even if you know the order of operations.
- Not Double-Checking Your Work: After you've finished solving the problem, take a moment to review your work and make sure you haven't made any mistakes.
To avoid these pitfalls, practice is key. The more you work through mathematical problems, the more comfortable you'll become with the order of operations, and the less likely you'll be to make mistakes.
Solving 3 x 3 - 3 / 3 + 3 Step-by-Step
Now that we've established a solid understanding of the order of operations, let's apply it to solve the equation 3 x 3 - 3 / 3 + 3.
- Multiplication: According to PEMDAS, we perform multiplication and division before addition and subtraction. So, we start with the multiplication:
3 x 3 = 9. The equation now becomes9 - 3 / 3 + 3. - Division: Next, we perform the division:
3 / 3 = 1. The equation now becomes9 - 1 + 3. - Subtraction: Now we move on to addition and subtraction, working from left to right. First, we subtract:
9 - 1 = 8. The equation now becomes8 + 3. - Addition: Finally, we perform the addition:
8 + 3 = 11.
Therefore, the solution to the equation 3 x 3 - 3 / 3 + 3 is 11.
Alternative Interpretations and Why They Are Incorrect
One of the reasons this equation often causes confusion is the potential for misinterpretation. Some might incorrectly try to perform the operations from left to right without regard to the order of operations. Let's explore why this approach is wrong:
If we were to solve the equation from left to right, we would get a different answer:
3 x 3 = 99 - 3 = 66 / 3 = 22 + 3 = 5
This incorrect method yields an answer of 5, which is significantly different from the correct answer of 11. This discrepancy highlights the critical importance of adhering to PEMDAS to ensure accurate and consistent results.
Another common mistake is to treat the division as if it applies to the entire expression to the left. For example, someone might incorrectly interpret 3 x 3 - 3 / 3 + 3 as 3 x 3 - (3 / 3) + 3. While the parentheses don't change the outcome in this specific case, it's still a misunderstanding of the order of operations. The division only applies to the numbers immediately to its left and right, unless parentheses indicate otherwise.
Trends and Latest Developments in Mathematical Education
Mathematical education is constantly evolving to better equip students with the skills and knowledge they need to succeed in an increasingly complex world. Here are some current trends and developments in the field:
- Emphasis on Conceptual Understanding: There's a growing emphasis on teaching mathematical concepts in a way that promotes deep understanding rather than rote memorization. This approach encourages students to think critically, make connections between different concepts, and apply their knowledge to real-world problems.
- Integration of Technology: Technology is playing an increasingly important role in mathematical education. Interactive software, online resources, and educational apps can help students visualize concepts, explore different scenarios, and receive personalized feedback.
- Focus on Problem-Solving Skills: Mathematical education is shifting away from a focus on procedural skills and towards a focus on problem-solving skills. Students are being challenged to solve open-ended problems that require them to apply their knowledge creatively and think outside the box.
- Personalized Learning: Personalized learning is becoming more prevalent in mathematical education. This approach involves tailoring instruction to meet the individual needs and learning styles of each student. Adaptive learning platforms can track student progress and provide customized content and feedback.
- Real-World Applications: There's a growing effort to connect mathematical concepts to real-world applications. By showing students how math is used in everyday life, educators can make the subject more engaging and relevant.
Professional Insights
As educators and professionals in STEM fields, we recognize that math anxiety is a real and significant issue for many students. It's crucial to create a supportive and encouraging learning environment where students feel comfortable asking questions and making mistakes. Emphasizing the importance of effort and perseverance over innate ability can help students build confidence and develop a growth mindset.
Moreover, we need to continually adapt our teaching methods to meet the changing needs of our students. This means incorporating technology, focusing on conceptual understanding, and providing opportunities for students to apply their knowledge in meaningful ways. By doing so, we can empower students to become confident and capable problem-solvers.
Tips and Expert Advice for Mastering Math Problems
Mastering math problems like 3 x 3 - 3 / 3 + 3 requires a combination of understanding the fundamental principles and developing effective problem-solving strategies. Here are some tips and expert advice to help you succeed:
- Build a Strong Foundation: Make sure you have a solid understanding of the basic concepts. Review the order of operations, fractions, decimals, percentages, and other fundamental topics. A strong foundation will make it easier to tackle more complex problems.
- Practice Regularly: The more you practice, the more comfortable you'll become with mathematical concepts and problem-solving techniques. Set aside time each day or week to work through problems.
- Break Down Complex Problems: When faced with a complex problem, break it down into smaller, more manageable steps. This will make the problem less daunting and easier to solve.
- Use Visual Aids: Visual aids like diagrams, charts, and graphs can help you visualize mathematical concepts and understand relationships between different quantities.
- Check Your Work: Always take the time to check your work and make sure you haven't made any mistakes. This can save you from losing points on exams or making errors in real-world applications.
- Seek Help When Needed: Don't be afraid to ask for help when you're struggling with a problem. Talk to your teacher, a tutor, or a classmate. There are also many online resources that can provide assistance.
- Understand the 'Why' Behind the 'How': It's not enough to simply memorize formulas and procedures. You need to understand why those formulas and procedures work. This will help you apply them more effectively and remember them for longer.
- Connect Math to Real-World Applications: Look for opportunities to connect mathematical concepts to real-world applications. This will make the subject more engaging and relevant. For example, you could use math to calculate the tip at a restaurant, plan a budget, or measure the area of a room.
- Embrace Mistakes as Learning Opportunities: Everyone makes mistakes, especially when learning something new. Don't get discouraged when you make a mistake. Instead, view it as an opportunity to learn and improve.
- Stay Organized: Keep your notes, homework, and other materials organized. This will make it easier to find what you need when you're studying or working on a problem.
Additional Strategies for Complex Equations
For more complex equations, consider these strategies:
- Rewrite the Equation: Sometimes, rewriting an equation can make it easier to understand and solve. For example, you might rewrite a fraction as a decimal or combine like terms.
- Use a Calculator: While it's important to understand the underlying concepts, a calculator can be a valuable tool for performing calculations quickly and accurately.
- Estimate the Answer: Before you start solving a problem, try to estimate the answer. This will give you a sense of whether your final answer is reasonable.
- Work Backwards: If you're stuck on a problem, try working backwards from the answer. This can sometimes help you identify the steps needed to solve the problem.
- Collaborate with Others: Working with others can be a great way to learn and improve your problem-solving skills. Discuss the problem with a classmate or study group and see if you can come up with a solution together.
FAQ About Order of Operations
Q: What does PEMDAS stand for?
A: PEMDAS stands for Parentheses, Exponents, Multiplication and Division (from left to right), and Addition and Subtraction (from left to right). It is a mnemonic used to remember the order of operations in mathematics.
Q: Why is the order of operations important?
A: The order of operations ensures that everyone arrives at the same answer when solving a mathematical problem. Without it, mathematical expressions would be ambiguous, and calculations would be unreliable.
Q: What do I do if an equation has both multiplication and division?
A: Perform multiplication and division from left to right, in the order they appear in the equation.
Q: What if there are parentheses inside parentheses?
A: Start with the innermost set of parentheses and work your way outwards.
Q: Can I use a calculator to solve problems involving the order of operations?
A: Yes, a calculator can be a valuable tool, but it's important to understand the underlying concepts first. Make sure your calculator is set to the correct mode and that you enter the equation correctly.
Conclusion
Mastering the order of operations is crucial for solving mathematical problems accurately and consistently. The equation 3 x 3 - 3 / 3 + 3 serves as a great example of how following PEMDAS leads to the correct solution. By understanding the principles, avoiding common pitfalls, and practicing regularly, you can build confidence and improve your problem-solving skills.
Now that you have a comprehensive understanding of the order of operations, put your knowledge to the test! Try solving similar equations and explore more complex mathematical problems. Share your insights and questions in the comments below, and let's continue learning together. Don't forget to share this article with anyone who might benefit from a clearer understanding of this fundamental mathematical principle.
Latest Posts
Latest Posts
-
How Can You Improve Your English
Nov 26, 2025
-
3 X 3 3 3 3
Nov 26, 2025
-
Spongy Bone Vs Compact Bone Histology
Nov 26, 2025
-
How Many Feet Is 80 Meters
Nov 26, 2025
-
What Is The Lcm For 10 And 8
Nov 26, 2025
Related Post
Thank you for visiting our website which covers about 3 X 3 - 3 / 3 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.