Number Of Prime Numbers Between 1 And 50
catholicpriest
Nov 26, 2025 · 11 min read
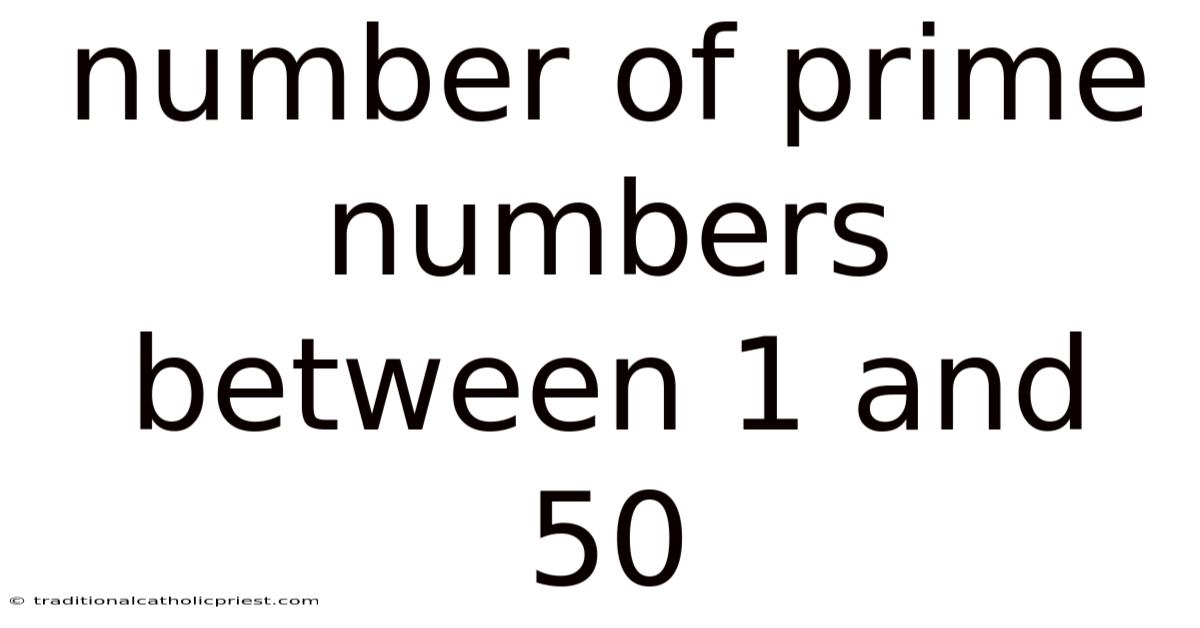
Table of Contents
Imagine you're organizing a grand mathematical party, and only the prime numbers are invited. You've sent out invitations to all numbers between 1 and 50, but you need to know exactly how many seats to set at the table. Determining the number of prime numbers within a given range is a fundamental concept in number theory, with practical applications ranging from cryptography to computer science.
In this mathematical quest, prime numbers stand out as the unique building blocks of all integers. Understanding their distribution and frequency is a puzzle that has captivated mathematicians for centuries. Specifically, discovering how many prime numbers reside between 1 and 50 is a journey through the core of number theory, revealing fascinating patterns and concepts that underpin much of modern mathematics.
Main Subheading
Prime numbers are the foundational elements of number theory, revered for their unique property of being divisible only by 1 and themselves. This characteristic distinguishes them from composite numbers, which have divisors other than 1 and themselves. The quest to understand and identify prime numbers has been a central theme in mathematics for millennia, inspiring algorithms, theorems, and countless hours of exploration.
The significance of prime numbers extends far beyond theoretical mathematics. Their unique properties make them indispensable in practical applications, particularly in the field of cryptography. Modern encryption methods, such as RSA, rely heavily on the difficulty of factoring large numbers into their prime components. This inherent complexity ensures that sensitive data remains secure, making prime numbers essential to digital security. Moreover, prime numbers play a critical role in computer science, where they are used in hashing algorithms, random number generation, and various other computational processes.
Comprehensive Overview
Delving into the world of prime numbers requires a clear definition and understanding of their properties. A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. The number 1 is not considered a prime number, as including it would complicate many theorems and algorithms in number theory. The first few prime numbers are 2, 3, 5, 7, 11, and so on.
The concept of prime numbers dates back to ancient Greece, with mathematicians like Euclid making significant contributions to their understanding. Euclid's Elements, written around 300 BC, contains the first known proof of the infinitude of prime numbers. This elegant proof demonstrates that no matter how many prime numbers one has found, it is always possible to find another one. Euclid's theorem is a cornerstone of number theory, underscoring the endless nature of prime numbers.
Sieve of Eratosthenes
One of the oldest and most intuitive methods for identifying prime numbers is the Sieve of Eratosthenes. This algorithm, named after the Greek mathematician Eratosthenes of Cyrene, provides a systematic way to find all prime numbers up to a specified limit. The Sieve works by iteratively marking the multiples of each prime number, starting with 2.
To apply the Sieve of Eratosthenes to find all prime numbers between 1 and 50, one would begin by listing all numbers from 2 to 50. The first number, 2, is prime, so we mark all multiples of 2 (4, 6, 8, ..., 50) as composite. The next unmarked number, 3, is prime, so we mark all multiples of 3 (6, 9, 12, ..., 48) as composite. We continue this process, marking multiples of 5, 7, and so on, up to the square root of 50, which is approximately 7. After completing these steps, the remaining unmarked numbers are the prime numbers within the range of 1 to 50.
Prime Number Theorem
The distribution of prime numbers is a topic of intense study in number theory. While prime numbers appear to be randomly scattered among the integers, there is an underlying order to their distribution. The Prime Number Theorem provides an approximation for the number of primes less than or equal to a given number n, denoted as π(n). The theorem states that π(n) is approximately n/ln(n), where ln(n) is the natural logarithm of n.
The Prime Number Theorem offers valuable insights into the density of prime numbers. It suggests that as n becomes larger, the proportion of numbers that are prime decreases. Although the theorem provides an approximation, it does not give an exact count of prime numbers within a specific range. The actual distribution of prime numbers can deviate significantly from the approximation, especially for smaller values of n.
Identifying Primes
Identifying whether a given number is prime requires testing its divisibility by smaller numbers. A straightforward approach is to check whether the number is divisible by any integer from 2 to the square root of the number. If no divisors are found, the number is prime. This method is effective for smaller numbers, but it becomes computationally intensive for very large numbers.
More sophisticated primality tests, such as the Miller-Rabin primality test and the AKS primality test, are used for larger numbers. These tests employ advanced mathematical concepts to determine primality with a high degree of certainty. The Miller-Rabin test, for example, is a probabilistic algorithm that can quickly identify composite numbers, while the AKS test is a deterministic algorithm that guarantees primality.
Importance of Prime Numbers
The importance of prime numbers extends beyond theoretical mathematics, with practical applications in various fields. In cryptography, prime numbers are essential for securing data transmission and storage. The RSA encryption algorithm, widely used for secure communication, relies on the difficulty of factoring large numbers into their prime components. The larger the prime numbers used, the more secure the encryption.
In computer science, prime numbers are used in hashing algorithms to distribute data evenly across hash tables. This helps to minimize collisions and improve the efficiency of data retrieval. Prime numbers are also used in random number generators to produce sequences of numbers that appear random but are generated deterministically. These generators are used in simulations, statistical analysis, and various other applications.
Trends and Latest Developments
The study of prime numbers remains an active area of research in mathematics. One of the most significant open problems is the Riemann Hypothesis, which concerns the distribution of prime numbers. The Riemann Hypothesis, formulated by Bernhard Riemann in 1859, proposes a specific pattern in the distribution of prime numbers. If proven, it would have profound implications for our understanding of number theory and its applications.
Recent developments in prime number research include the discovery of new methods for finding large prime numbers and improving primality tests. The Great Internet Mersenne Prime Search (GIMPS) project, a collaborative effort involving thousands of volunteers, has discovered many of the largest known prime numbers. These discoveries push the boundaries of computational mathematics and contribute to our understanding of the distribution of prime numbers.
Real-World Impact
The practical applications of prime numbers continue to expand with advancements in technology. In cybersecurity, stronger encryption algorithms are needed to protect against increasingly sophisticated cyber threats. Prime numbers play a critical role in developing these algorithms, ensuring that sensitive data remains secure.
In data science, prime numbers are used in advanced machine learning models to improve the accuracy and efficiency of data analysis. Prime numbers help to optimize algorithms, reduce computational complexity, and enhance the overall performance of machine learning systems. As data becomes increasingly valuable, the importance of prime numbers in data science will continue to grow.
Professional Insights
Professionals in mathematics, computer science, and cryptography rely on a deep understanding of prime numbers to solve complex problems. Mathematicians explore the theoretical properties of prime numbers, developing new theorems and algorithms. Computer scientists use prime numbers to design efficient data structures and algorithms. Cryptographers employ prime numbers to create secure encryption methods.
Staying up-to-date with the latest developments in prime number research is essential for professionals in these fields. New discoveries and advancements can have a significant impact on their work, leading to improved algorithms, stronger encryption, and more efficient data analysis techniques. Continuous learning and collaboration are key to leveraging the power of prime numbers in real-world applications.
Tips and Expert Advice
Understanding and working with prime numbers can be enhanced through various strategies. Whether you are a student, a researcher, or a professional, these tips can help you deepen your knowledge and improve your skills.
Tip 1: Master the Fundamentals Start with a solid understanding of the basic definitions and theorems related to prime numbers. Ensure you know what prime numbers are, how they differ from composite numbers, and the significance of Euclid's theorem on the infinitude of primes. Understanding the Sieve of Eratosthenes is also crucial for identifying prime numbers within a given range.
To reinforce your understanding, practice identifying prime numbers using the Sieve of Eratosthenes for different ranges. Work through examples and exercises to solidify your knowledge of the fundamental concepts. Consider exploring resources like textbooks, online courses, and educational websites to deepen your understanding.
Tip 2: Explore Advanced Concepts Once you have a firm grasp of the basics, delve into more advanced topics such as the Prime Number Theorem and the Riemann Hypothesis. Understanding these concepts will provide deeper insights into the distribution and behavior of prime numbers. Explore different primality tests, such as the Miller-Rabin test and the AKS test, to understand how to efficiently determine whether a large number is prime.
Engage in discussions and collaborations with other mathematicians or researchers to explore these advanced concepts. Attend seminars, workshops, and conferences to learn about the latest developments in prime number research. Reading research papers and academic articles can also help you stay up-to-date with the cutting edge of the field.
Tip 3: Use Computational Tools Leverage computational tools and programming languages to explore and analyze prime numbers. Use programming languages like Python, Mathematica, or MATLAB to implement algorithms for identifying prime numbers, testing primality, and exploring their distribution. Computational tools can help you visualize prime number patterns and gain a deeper understanding of their behavior.
Experiment with different algorithms and techniques to find the most efficient ways to identify and analyze prime numbers. Use computational tools to explore the distribution of prime numbers within large ranges and test the accuracy of the Prime Number Theorem. Consider contributing to open-source projects related to prime number research or developing your own tools for analyzing prime numbers.
Tip 4: Apply Prime Numbers in Real-World Scenarios Understand how prime numbers are used in practical applications such as cryptography, computer science, and data science. Explore the RSA encryption algorithm and learn how prime numbers are used to secure data transmission and storage. Investigate how prime numbers are used in hashing algorithms and random number generators.
Look for opportunities to apply your knowledge of prime numbers in real-world projects or applications. Consider developing a secure communication system using prime number-based encryption or designing an efficient hashing algorithm using prime numbers. By applying your knowledge in practical scenarios, you can gain valuable experience and contribute to solving real-world problems.
FAQ
Q: What is a prime number? A: A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself.
Q: Why are prime numbers important? A: Prime numbers are fundamental in number theory and have critical applications in cryptography, computer science, and data science.
Q: How can I identify prime numbers? A: You can use the Sieve of Eratosthenes or test divisibility by numbers up to the square root of the number in question.
Q: What is the Prime Number Theorem? A: The Prime Number Theorem provides an approximation for the number of primes less than or equal to a given number n, denoted as π(n), approximately n/ln(n).
Q: What is the Riemann Hypothesis? A: The Riemann Hypothesis is a famous unsolved problem in mathematics concerning the distribution of prime numbers.
Q: What are the first 10 prime numbers? A: The first 10 prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23, and 29.
Q: How many prime numbers are there between 1 and 50? A: There are 15 prime numbers between 1 and 50. They are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, and 47.
Conclusion
Prime numbers, those elusive yet foundational building blocks of mathematics, play a critical role in various fields, from securing our digital communications to optimizing data analysis. Understanding their distribution, properties, and applications is essential for mathematicians, computer scientists, and anyone interested in the beauty and power of numbers.
Now that you've journeyed through the world of prime numbers, what's your next step? Dive deeper into the Riemann Hypothesis, explore advanced encryption techniques, or simply share your newfound knowledge with others. Leave a comment below with your thoughts or questions, and let's continue the exploration together!
Latest Posts
Latest Posts
-
Cool Words That Begin With L
Nov 26, 2025
-
Is Hydrogen Bonding A Covalent Bond
Nov 26, 2025
-
How Do You Spell Number 13
Nov 26, 2025
-
Is Blue Eyes Dominant Or Recessive
Nov 26, 2025
-
Number Of Prime Numbers Between 1 And 50
Nov 26, 2025
Related Post
Thank you for visiting our website which covers about Number Of Prime Numbers Between 1 And 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.