Is 1 5/8 Bigger Than 1 1/2
catholicpriest
Nov 27, 2025 · 11 min read
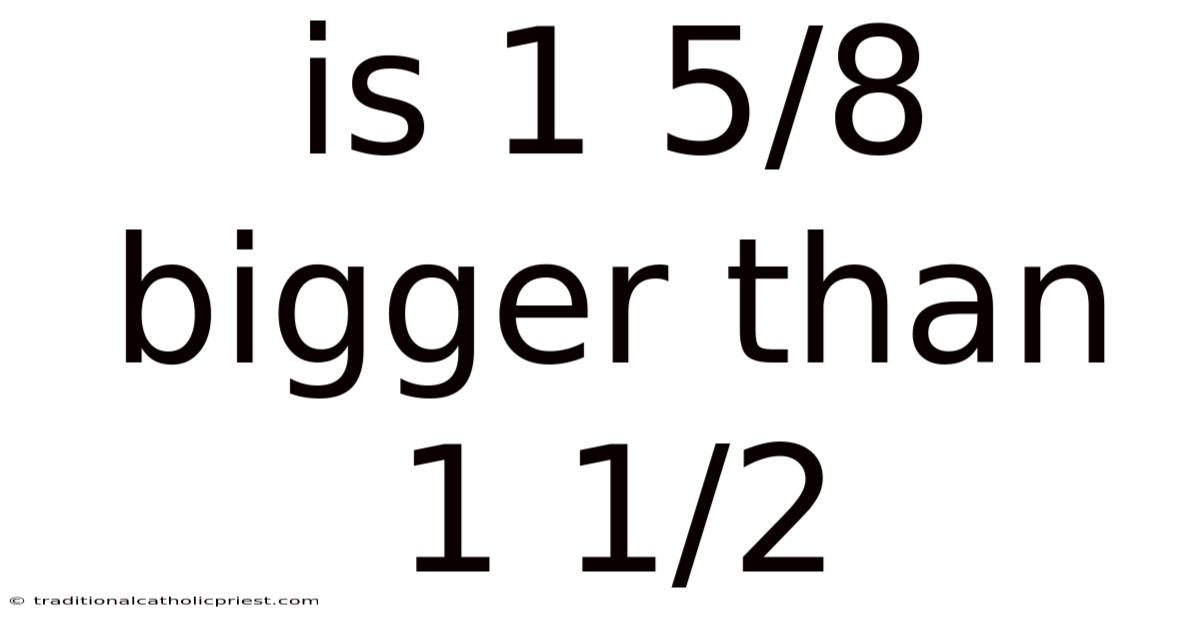
Table of Contents
Imagine you're baking a cake and the recipe calls for 1 1/2 cups of flour. You grab your measuring cup and fill it up, but then you spot another recipe that requires 1 5/8 cups of sugar. Suddenly, you're faced with a simple yet crucial question: do you need more sugar than flour? This everyday scenario highlights how understanding fractions and comparing their values is essential, not just in the kitchen but in countless real-life situations.
The ability to quickly and accurately determine whether 1 5/8 is bigger than 1 1/2 is a fundamental skill in mathematics. It's more than just comparing numbers; it's about understanding proportions, quantities, and how they relate to each other. Whether you're a student tackling homework, a professional working with precise measurements, or simply managing household tasks, this skill is invaluable. In this article, we will explore different methods to compare these fractions, providing you with the knowledge and confidence to tackle similar questions with ease.
Main Subheading: Understanding Fractions and Mixed Numbers
Before diving into the comparison, let’s ensure we have a solid grasp of what fractions and mixed numbers represent. A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, and the numerator indicates how many of those parts we have. For example, in the fraction 1/2, the whole is divided into two equal parts, and we have one of those parts.
A mixed number, on the other hand, is a combination of a whole number and a fraction. It represents a quantity greater than one whole. In our case, both 1 5/8 and 1 1/2 are mixed numbers. The whole number part tells us how many complete units we have, and the fraction part tells us how much of an additional unit we have. Understanding this distinction is crucial for accurately comparing these quantities. When comparing mixed numbers, the whole number parts are compared first, and if they are equal, then the fractional parts are compared. This foundational knowledge allows us to move forward with confidence in our comparison.
Comprehensive Overview: Methods to Compare 1 5/8 and 1 1/2
There are several methods we can use to determine whether 1 5/8 is bigger than 1 1/2. Each method offers a different perspective and can be useful depending on the context and your comfort level with mathematical operations. Let's explore these methods in detail:
-
Converting to Improper Fractions: One of the most reliable methods is to convert both mixed numbers into improper fractions. An improper fraction is a fraction where the numerator is greater than or equal to the denominator. To convert a mixed number to an improper fraction, multiply the whole number by the denominator and add the numerator. The result becomes the new numerator, and the denominator remains the same.
For 1 5/8, we multiply 1 (the whole number) by 8 (the denominator) which equals 8. Then we add 5 (the numerator) to get 13. So, 1 5/8 converted to an improper fraction is 13/8.
For 1 1/2, we multiply 1 (the whole number) by 2 (the denominator) which equals 2. Then we add 1 (the numerator) to get 3. So, 1 1/2 converted to an improper fraction is 3/2.
Now we need to compare 13/8 and 3/2. To do this, we can find a common denominator. The least common multiple of 8 and 2 is 8. So we convert 3/2 to an equivalent fraction with a denominator of 8. To do this, we multiply both the numerator and denominator of 3/2 by 4, resulting in 12/8.
Comparing 13/8 and 12/8, it’s clear that 13/8 is greater than 12/8 because 13 is greater than 12. Therefore, 1 5/8 is bigger than 1 1/2.
-
Finding a Common Denominator Directly: Another approach is to directly compare the fractional parts of the mixed numbers by finding a common denominator. Since both mixed numbers have a whole number of 1, we only need to compare 5/8 and 1/2. As we determined in the previous method, the least common multiple of 8 and 2 is 8. We convert 1/2 to an equivalent fraction with a denominator of 8 by multiplying both the numerator and the denominator by 4, resulting in 4/8. Now we compare 5/8 and 4/8. Since 5 is greater than 4, 5/8 is greater than 4/8, which means 1 5/8 is bigger than 1 1/2.
-
Converting to Decimals: Converting fractions to decimals is another straightforward method for comparison. To convert a fraction to a decimal, simply divide the numerator by the denominator.
For 1 5/8, we first focus on the fraction 5/8. Dividing 5 by 8, we get 0.625. So, 1 5/8 as a decimal is 1 + 0.625 = 1.625.
For 1 1/2, we focus on the fraction 1/2. Dividing 1 by 2, we get 0.5. So, 1 1/2 as a decimal is 1 + 0.5 = 1.5.
Comparing 1.625 and 1.5, it’s clear that 1.625 is greater than 1.5. Therefore, 1 5/8 is bigger than 1 1/2.
-
Visual Representation: Sometimes, visualizing fractions can make the comparison more intuitive. Imagine two identical pies. One pie is divided into 8 equal slices, and you have 5 of those slices (representing 5/8). The other pie is divided into 2 equal slices, and you have 1 of those slices (representing 1/2). If you combine these fractions with a whole pie each, it becomes clear that having 1 whole pie plus 5 slices of the first pie is more than having 1 whole pie plus 1 slice of the second pie, because each slice of the first pie is smaller, and you have more of them. This visual representation can be particularly helpful for those who are more visually oriented.
-
Benchmark Fractions: Using benchmark fractions can provide a quick estimate and help in comparison. Benchmark fractions are common fractions like 1/4, 1/3, 1/2, 2/3, and 3/4, which are easy to visualize and remember. We know that 1/2 is equal to 4/8. Therefore, 1 1/2 is the same as 1 4/8. Now, we can easily see that 1 5/8 is slightly more than 1 1/2 because 5/8 is greater than 4/8. This method can be particularly useful for making quick estimations without performing exact calculations.
Each of these methods provides a reliable way to compare 1 5/8 and 1 1/2. The best method to use depends on your personal preference, the context of the problem, and the tools available to you.
Trends and Latest Developments
In recent years, there's been a growing emphasis on improving numeracy skills, especially among students and adults. Studies have shown that a strong understanding of fractions is a key predictor of success in algebra and higher-level mathematics. As a result, educators are increasingly focusing on hands-on activities and visual aids to help students develop a deeper understanding of fractions.
Online educational platforms and apps have also played a significant role in making fraction comparison more accessible. These tools often provide interactive exercises and immediate feedback, allowing learners to practice and improve their skills at their own pace. Furthermore, many of these platforms incorporate gamification elements to make learning more engaging and enjoyable.
In the professional world, accurate fraction comparison is crucial in various fields, including construction, engineering, and finance. For example, architects and engineers need to work with precise measurements to ensure the structural integrity of buildings. Similarly, financial analysts need to compare fractions when calculating investment returns and managing risk.
According to a recent survey, a significant percentage of adults struggle with basic fraction-related tasks. This highlights the importance of continued education and practice to maintain and improve numeracy skills. The ability to confidently compare fractions is not just an academic skill; it's a practical skill that can impact everyday life and career opportunities.
Tips and Expert Advice
Comparing fractions doesn’t have to be a daunting task. Here are some practical tips and expert advice to help you master this skill:
-
Practice Regularly: Like any skill, proficiency in comparing fractions comes with practice. Dedicate some time each day to work on fraction-related exercises. Start with simple comparisons and gradually move on to more complex problems. Consistent practice will build your confidence and improve your accuracy.
- Use online resources, textbooks, or create your own practice problems. The key is to expose yourself to a variety of scenarios and challenges.
- Consider setting small, achievable goals for each practice session. For example, aim to solve five fraction comparison problems correctly in a row.
-
Understand the Concept of Equivalence: A strong understanding of equivalent fractions is crucial for comparison. Remember that multiplying or dividing both the numerator and denominator of a fraction by the same number does not change its value.
- Use visual aids, such as fraction bars or pie charts, to illustrate the concept of equivalence.
- Practice finding equivalent fractions for various common fractions, such as 1/2, 1/3, and 1/4.
-
Use Real-Life Examples: Connect fraction comparison to real-life situations to make it more relatable and meaningful. Think about scenarios like cooking, baking, measuring ingredients, or splitting a pizza among friends.
- When following a recipe, pay attention to the fractions used and try to mentally compare them.
- When sharing something with others, think about how you can divide it into equal parts and express those parts as fractions.
-
Master the Art of Estimation: Developing the ability to estimate fraction values can be a valuable tool for quick comparisons. Use benchmark fractions as reference points and try to approximate the values of other fractions relative to these benchmarks.
- For example, if you need to compare 3/7 and 1/2, you can estimate that 3/7 is slightly less than 1/2 because 3 is slightly less than half of 7.
- Practice estimating fraction values in everyday situations, such as when shopping or measuring distances.
-
Don't Be Afraid to Use Tools: There are many tools available to help you compare fractions, including calculators, online converters, and educational apps. Don't hesitate to use these tools when needed, especially when dealing with complex fractions.
- Familiarize yourself with the features of your calculator and how to use it to perform fraction-related calculations.
- Explore different online resources and apps to find tools that suit your learning style and preferences.
By following these tips and expert advice, you can significantly improve your ability to compare fractions and gain a deeper understanding of numerical concepts.
FAQ: Frequently Asked Questions About Fraction Comparison
Q: Why is it important to know how to compare fractions?
A: Comparing fractions is a fundamental skill in mathematics with practical applications in various fields, including cooking, construction, finance, and more. It helps in making informed decisions and solving real-world problems that involve proportions and quantities.
Q: What is the easiest method to compare fractions?
A: The easiest method depends on individual preferences and the specific fractions being compared. Converting to decimals or finding a common denominator are generally considered straightforward methods for many people.
Q: How do I find a common denominator?
A: To find a common denominator, determine the least common multiple (LCM) of the denominators of the fractions you want to compare. The LCM is the smallest number that is a multiple of both denominators. You can then convert each fraction to an equivalent fraction with the common denominator.
Q: What if the fractions have different whole numbers?
A: If the mixed numbers have different whole numbers, you only need to compare the whole numbers. The mixed number with the larger whole number is the greater number. If the whole numbers are the same, then you need to compare the fractional parts.
Q: Can I use a calculator to compare fractions?
A: Yes, calculators can be very helpful for comparing fractions. Most calculators have a fraction function that allows you to enter fractions and perform calculations. Some calculators can also convert fractions to decimals, which can make comparison easier.
Conclusion
In summary, determining whether 1 5/8 is bigger than 1 1/2 involves understanding the fundamentals of fractions and applying various comparison methods. Whether you choose to convert to improper fractions, find a common denominator, convert to decimals, use visual representations, or rely on benchmark fractions, the key is to approach the problem with a clear understanding of the underlying concepts.
Mastering the skill of fraction comparison not only enhances your mathematical abilities but also empowers you to make informed decisions in everyday situations. By practicing regularly, understanding equivalent fractions, using real-life examples, and leveraging available tools, you can confidently tackle any fraction-related challenge.
Now that you've gained a comprehensive understanding of fraction comparison, put your knowledge to the test! Try comparing other fractions and mixed numbers, and challenge yourself with increasingly complex problems. Share this article with friends or family who might benefit from it, and let's work together to build a stronger understanding of mathematics. Leave a comment below sharing your favorite method for comparing fractions or any tips you've found helpful. Your insights can help others on their mathematical journey!
Latest Posts
Latest Posts
-
What Is The Row Space Of A Matrix
Nov 27, 2025
-
How Many Valence Electrons Are In Iodine
Nov 27, 2025
-
How Many Miles Is One Click
Nov 27, 2025
-
Five Letter Words That End In W
Nov 27, 2025
-
Words Starting With The Same Sound
Nov 27, 2025
Related Post
Thank you for visiting our website which covers about Is 1 5/8 Bigger Than 1 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.