3 7 Times 2 1 2
catholicpriest
Nov 08, 2025 · 12 min read
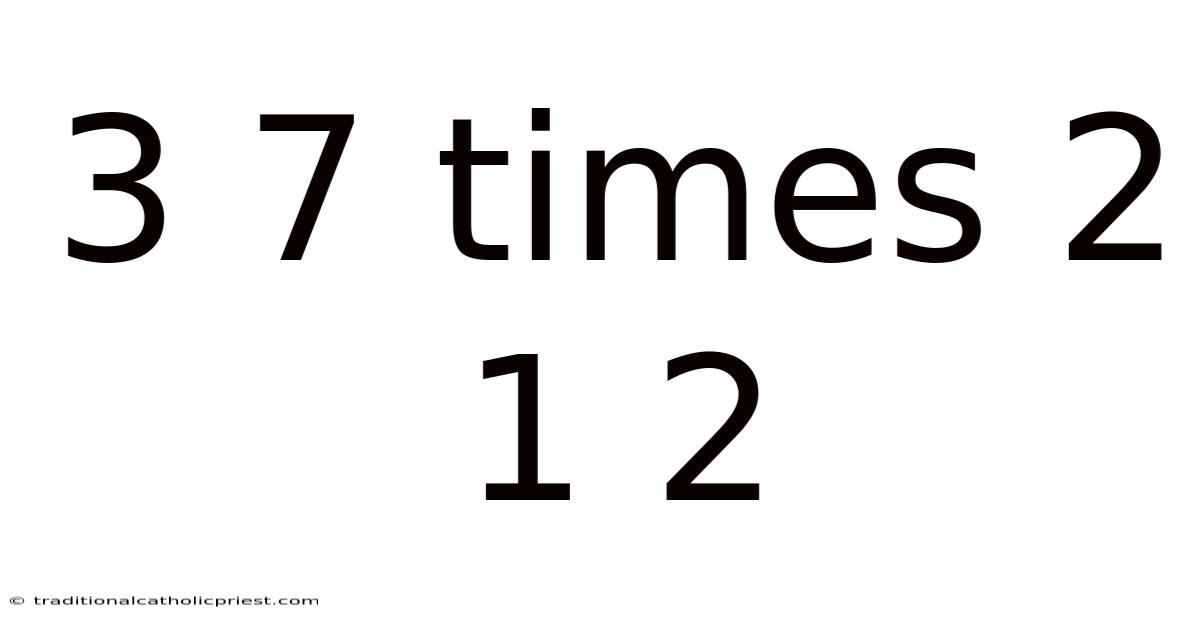
Table of Contents
Imagine you're teaching a child the basics of multiplication. You start with simple examples, like "2 times 2," which is easy to visualize as two groups of two objects. But as the numbers grow, the process becomes more abstract. Suddenly, you're faced with a question that seems daunting: What is 3.7 times 2.12? This isn't a simple calculation you can do in your head; it requires careful attention to detail and a solid understanding of decimal multiplication.
Decimal multiplication, while seemingly complex at first glance, is a fundamental skill in mathematics with applications in numerous real-world scenarios. Whether you're calculating grocery bills, measuring ingredients for a recipe, or figuring out the area of a room, understanding how to multiply decimals accurately is essential. In this comprehensive guide, we'll break down the process of multiplying 3.7 by 2.12, explore the underlying principles, discuss common pitfalls, and provide practical tips to master this skill. We'll also delve into the trends and latest developments in decimal multiplication, answer frequently asked questions, and leave you with a clear call to action to further enhance your mathematical abilities. So, let's embark on this mathematical journey together and unlock the secrets of decimal multiplication!
Main Subheading
Decimal multiplication extends the concept of whole number multiplication to include numbers with decimal points. This is crucial because many real-world measurements and values are not whole numbers. Think about the price of gasoline, the weight of produce at the grocery store, or the dimensions of a piece of land – all these often involve decimals. Without the ability to accurately multiply decimals, we would struggle to perform many everyday calculations.
The process involves several steps, including setting up the multiplication problem, performing the multiplication as if the numbers were whole numbers, and then carefully placing the decimal point in the correct position in the final answer. This last step is where many people make mistakes, so it's important to understand the logic behind it. By mastering decimal multiplication, you gain a valuable skill that empowers you to solve a wide range of problems with confidence and precision. Let's dive deeper into the comprehensive overview to understand the scientific foundations, historical context, and essential concepts related to the topic.
Comprehensive Overview
Decimal multiplication is a crucial arithmetic operation that builds upon the principles of whole number multiplication. At its core, it's about finding the total when a number (the multiplicand) is added to itself a certain number of times (the multiplier), but with the added complexity of decimal points. Understanding the underlying mathematical concepts and the history behind decimal notation can significantly enhance your ability to perform decimal multiplication accurately.
Definitions and Scientific Foundations
A decimal is a number that uses a decimal point to separate the whole number part from the fractional part. For example, in the number 3.7, "3" is the whole number part, and "7" represents seven-tenths. The decimal point indicates that the digits to its right represent fractions with denominators that are powers of 10 (10, 100, 1000, etc.).
The scientific foundation of decimal multiplication lies in the principles of place value and the distributive property of multiplication. Place value dictates that the position of a digit in a number determines its value. In 3.7, the "3" represents 3 ones, and the "7" represents 7 tenths. The distributive property allows us to break down complex multiplication problems into simpler parts. For example, multiplying 3.7 by 2.12 can be seen as multiplying 3.7 by 2, then by 0.1, and then by 0.02, and adding the results together.
History of Decimal Notation
The concept of decimal notation has evolved over centuries. Ancient civilizations like the Egyptians and Babylonians used various systems to represent fractions, but none were as efficient and universally applicable as the decimal system we use today. The decimal system we use today is largely attributed to Simon Stevin, a Flemish mathematician who wrote a book called "De Thiende" (The Tenth) in 1585. Stevin advocated for the use of decimal fractions in everyday calculations, making arithmetic more accessible and practical. While he wasn't the first to conceive of decimal fractions, he was instrumental in popularizing their use.
Before Stevin, mathematicians often used sexagesimal (base-60) fractions, a system inherited from the Babylonians. While useful for astronomical calculations, sexagesimal fractions were cumbersome for everyday arithmetic. Stevin's advocacy for decimal fractions marked a significant step towards standardizing numerical notation and facilitating trade, science, and engineering.
Essential Concepts for Decimal Multiplication
To master decimal multiplication, it's essential to understand the following concepts:
- Place Value: Understanding the value of each digit based on its position relative to the decimal point.
- Decimal Point Placement: Knowing how to correctly place the decimal point in the final product. This is typically done by counting the total number of decimal places in the factors and placing the decimal point that many places from the right in the product.
- Distributive Property: Using the distributive property to break down complex multiplication problems into simpler, manageable parts.
- Estimation: Estimating the answer before performing the multiplication to check if the final result is reasonable.
Multiplying 3.7 by 2.12: A Step-by-Step Guide
Now, let's apply these concepts to the specific problem: 3.7 times 2.12.
-
Set up the problem: Write the numbers vertically, aligning them as if they were whole numbers.
2.12 x 3.7 ------ -
Multiply as if they were whole numbers: Ignore the decimal points and multiply 212 by 37.
212 x 37 ------ 1484 (212 x 7) 6360 (212 x 30) ------ 7844 -
Count the decimal places: Count the total number of digits to the right of the decimal points in both factors. In this case, 3.7 has one decimal place, and 2.12 has two decimal places, for a total of three decimal places.
-
Place the decimal point in the product: Starting from the rightmost digit in the product (7844), count three places to the left and place the decimal point.
7.844
Therefore, 3.7 times 2.12 equals 7.844.
Common Mistakes and How to Avoid Them
One of the most common mistakes in decimal multiplication is incorrectly placing the decimal point in the final answer. This often happens when people forget to count all the decimal places in the factors or when they count from the wrong direction.
Another common mistake is misaligning the numbers during the multiplication process, especially when dealing with multiple digits. This can lead to errors in the intermediate calculations and ultimately affect the accuracy of the final result.
To avoid these mistakes, it's essential to:
- Double-check the decimal point placement: Always count the decimal places carefully and verify that the decimal point is in the correct position in the product.
- Align the numbers carefully: Use graph paper or a ruler to ensure that the numbers are properly aligned during the multiplication process.
- Estimate the answer: Before performing the multiplication, estimate the answer to get a rough idea of what the final result should be. This can help you identify potential errors in your calculations.
Trends and Latest Developments
While the fundamental principles of decimal multiplication remain unchanged, there are some interesting trends and developments in how we approach and teach this skill. With the increasing reliance on technology, calculators and computer software have become indispensable tools for performing complex calculations, including decimal multiplication. However, there is a growing emphasis on developing mental math skills and a deeper understanding of mathematical concepts, rather than simply relying on technology to get the answer.
Educational Apps and Online Resources: Many educational apps and online resources offer interactive tutorials and practice exercises to help students learn and master decimal multiplication. These resources often incorporate gamification elements to make learning more engaging and enjoyable.
Emphasis on Conceptual Understanding: Educators are increasingly focusing on teaching the underlying concepts of decimal multiplication, rather than just rote memorization of rules and procedures. This approach helps students develop a deeper understanding of the material and apply it to real-world problems.
Integration with Other Mathematical Topics: Decimal multiplication is being integrated with other mathematical topics, such as fractions, percentages, and algebra, to provide students with a more holistic understanding of mathematics.
Use of Visual Aids and Manipulatives: Visual aids and manipulatives, such as base-ten blocks and number lines, are being used to help students visualize the process of decimal multiplication and develop a better understanding of the underlying concepts.
Professional Insights: From a professional standpoint, the ability to perform accurate decimal multiplication is essential in fields such as finance, engineering, and science. Financial analysts use decimal multiplication to calculate interest rates and investment returns, engineers use it to design structures and machines, and scientists use it to analyze data and conduct experiments. In these fields, accuracy and precision are paramount, and even small errors in decimal multiplication can have significant consequences.
Tips and Expert Advice
Mastering decimal multiplication involves more than just memorizing rules and procedures. It requires a solid understanding of the underlying concepts, consistent practice, and the application of effective strategies. Here are some practical tips and expert advice to help you enhance your skills and perform decimal multiplication with confidence:
-
Start with a Strong Foundation: Before tackling decimal multiplication, ensure that you have a solid understanding of whole number multiplication and place value. Review these concepts if needed to build a strong foundation for learning decimal multiplication.
-
Practice Regularly: Like any mathematical skill, decimal multiplication requires consistent practice to master. Set aside time each day or week to work on decimal multiplication problems, starting with simpler examples and gradually progressing to more complex ones. Regular practice will help you build confidence and improve your accuracy.
-
Use Estimation to Check Your Answers: Before performing the multiplication, estimate the answer to get a rough idea of what the final result should be. This can help you identify potential errors in your calculations. For example, if you are multiplying 3.7 by 2.12, you can estimate the answer by multiplying 4 by 2, which gives you 8. If your final answer is significantly different from 8, you know that you have made a mistake somewhere.
-
Break Down Complex Problems: When faced with a complex decimal multiplication problem, break it down into simpler, more manageable parts. Use the distributive property to multiply each digit separately and then add the results together. This approach can make the problem less daunting and reduce the likelihood of errors.
-
Use Graph Paper to Align Numbers: Misalignment of numbers is a common cause of errors in decimal multiplication. To avoid this, use graph paper to keep the numbers properly aligned during the multiplication process. This will help you keep track of the digits and reduce the risk of making mistakes.
-
Double-Check Your Work: Always double-check your work to ensure that you have not made any mistakes. Review each step of the multiplication process, paying close attention to decimal point placement and alignment of numbers. If possible, use a calculator to verify your answer.
-
Visualize the Process: Try to visualize the process of decimal multiplication to develop a deeper understanding of the underlying concepts. Use visual aids, such as number lines and base-ten blocks, to represent the numbers and the multiplication process. This can help you make sense of the abstract concepts and improve your understanding.
-
Seek Help When Needed: Don't be afraid to seek help from teachers, tutors, or online resources if you are struggling with decimal multiplication. There are many resources available to help you learn and master this skill, so don't hesitate to take advantage of them.
FAQ
Here are some frequently asked questions about decimal multiplication:
Q: Why is decimal multiplication important?
A: Decimal multiplication is important because it allows us to perform accurate calculations with numbers that are not whole numbers. This is essential in many real-world scenarios, such as calculating grocery bills, measuring ingredients for a recipe, and figuring out the area of a room.
Q: How do I place the decimal point in the answer?
A: To place the decimal point in the answer, count the total number of digits to the right of the decimal points in both factors. Then, starting from the rightmost digit in the product, count that many places to the left and place the decimal point.
Q: What is the distributive property of multiplication?
A: The distributive property of multiplication states that multiplying a number by a sum or difference is the same as multiplying the number by each term separately and then adding or subtracting the results. This property can be used to break down complex multiplication problems into simpler parts.
Q: How can I estimate the answer to a decimal multiplication problem?
A: To estimate the answer to a decimal multiplication problem, round the numbers to the nearest whole number or tenth and then perform the multiplication. This will give you a rough idea of what the final result should be.
Q: What are some common mistakes to avoid in decimal multiplication?
A: Some common mistakes to avoid in decimal multiplication include incorrectly placing the decimal point, misaligning the numbers during the multiplication process, and forgetting to carry over digits.
Conclusion
In conclusion, understanding and mastering decimal multiplication is an essential skill with far-reaching applications in everyday life and various professional fields. Throughout this article, we have explored the fundamental principles of decimal multiplication, examined its historical context, and provided a step-by-step guide to multiplying 3.7 by 2.12. We have also discussed common mistakes to avoid, shared practical tips and expert advice, and answered frequently asked questions.
By following the strategies and techniques outlined in this guide, you can enhance your skills and perform decimal multiplication with confidence and accuracy. Remember to practice regularly, use estimation to check your answers, and seek help when needed.
Now that you have a solid understanding of decimal multiplication, take the next step and put your knowledge into practice. Try solving more complex decimal multiplication problems, explore real-world applications of this skill, and share your newfound knowledge with others. Let's continue to explore the fascinating world of mathematics and unlock the power of numbers together!
Latest Posts
Latest Posts
-
How To Add Negative Fractions With Positive Fractions
Nov 08, 2025
-
What Is The Past Tense For Dream
Nov 08, 2025
-
How Do You Change Slope Intercept Form Into Standard Form
Nov 08, 2025
-
How Are Phospholipids Arranged In The Cell Membrane
Nov 08, 2025
-
Size Of A Virus Compared To Bacteria
Nov 08, 2025
Related Post
Thank you for visiting our website which covers about 3 7 Times 2 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.