Which Number Is A Factor Of 8
catholicpriest
Nov 17, 2025 · 9 min read
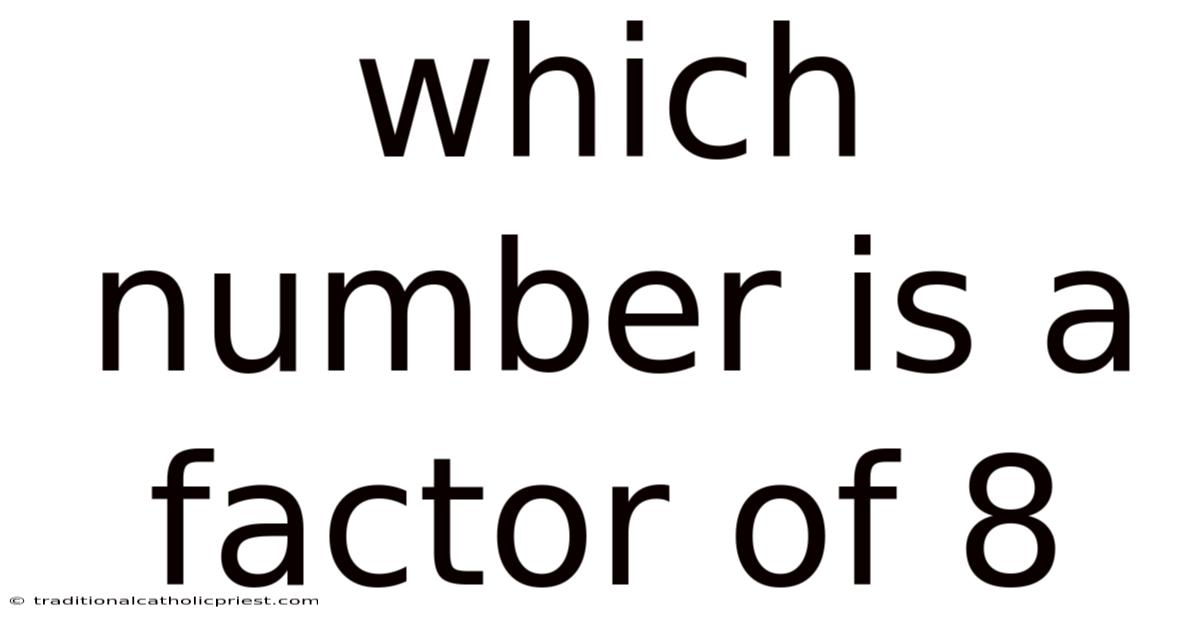
Table of Contents
Imagine you're at a bake sale, surrounded by tables laden with cookies, brownies, and cakes. You've got eight delicious cookies to divide equally into bags for your friends. Can you split them perfectly among two friends? How about four? What if only one very lucky friend gets all the cookies? Understanding how numbers divide evenly into others is the essence of factors, a fundamental concept in math that simplifies everything from sharing cookies to more complex calculations.
Delving into the world of mathematics often feels like unlocking a secret code to the universe. One of the most basic, yet surprisingly powerful, elements of this code is the concept of factors. Factors are the building blocks that help us understand the composition of numbers, and they play a crucial role in various mathematical operations, from simplifying fractions to solving complex equations. When we ask, "Which number is a factor of 8?" we're essentially asking which numbers can divide 8 evenly, without leaving a remainder. This seemingly simple question opens the door to a broader understanding of number theory and its practical applications.
Main Subheading
Factors are the numbers that divide evenly into another number. In simpler terms, when you multiply two factors together, you get the original number. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12 because each of these numbers divides 12 without leaving a remainder. Understanding factors is fundamental to many mathematical concepts, including prime factorization, greatest common factor (GCF), and least common multiple (LCM).
The concept of factors is deeply rooted in the foundations of arithmetic and number theory. It provides a structured way to break down numbers into their constituent parts, which simplifies complex calculations and problem-solving. By identifying factors, we can better understand the relationships between numbers and their divisibility properties. This knowledge is invaluable in various fields, from basic math to advanced engineering and computer science.
Comprehensive Overview
The concept of factors is not just a mathematical abstraction; it has practical applications that extend far beyond the classroom. Understanding factors can help in everyday tasks such as dividing quantities equally, planning schedules, and even understanding financial calculations. Factors are essential for simplifying fractions, finding common denominators, and solving algebraic equations. They also play a crucial role in cryptography and data compression algorithms used in computer science.
The history of factors can be traced back to ancient civilizations where mathematics was essential for trade, construction, and astronomy. Early mathematicians like the Babylonians and Egyptians developed methods for finding factors to solve practical problems related to land division, taxation, and calendar systems. The Greek mathematicians, particularly Euclid, formalized many of these concepts in his seminal work, The Elements, which laid the groundwork for modern number theory. Over centuries, the understanding and application of factors have evolved, becoming a cornerstone of mathematical thought.
At its core, a factor is a number that divides another number evenly, resulting in no remainder. For example, if we divide 8 by 2, we get 4, with no remainder. Therefore, 2 is a factor of 8. Similarly, 4 is a factor of 8 because 8 divided by 4 is 2, again with no remainder. Factors always come in pairs; in this case, 2 and 4 are a factor pair of 8. Recognizing these pairs can simplify the process of identifying all the factors of a number.
To determine whether a number is a factor of 8, we simply divide 8 by that number and check if the result is a whole number. If it is, then the number is a factor of 8. For instance, let’s check if 3 is a factor of 8. When we divide 8 by 3, we get 2.666…, which is not a whole number. Therefore, 3 is not a factor of 8. On the other hand, if we divide 8 by 1, we get 8, which is a whole number, making 1 a factor of 8. This process is straightforward and can be applied to any number to find its factors.
The factors of 8 are 1, 2, 4, and 8. This means that each of these numbers divides 8 evenly:
- 8 ÷ 1 = 8
- 8 ÷ 2 = 4
- 8 ÷ 4 = 2
- 8 ÷ 8 = 1
Each division results in a whole number, confirming that 1, 2, 4, and 8 are indeed the factors of 8. Understanding this concept is crucial for more advanced mathematical operations and problem-solving.
Trends and Latest Developments
In recent years, there has been a renewed focus on number theory and its applications in cryptography and computer science. The ability to quickly and efficiently find factors, especially of large numbers, is critical for securing digital communications and protecting sensitive data. This has led to the development of advanced algorithms and computational techniques for prime factorization.
One of the significant trends is the use of quantum computing to tackle factorization problems. Quantum computers, which leverage the principles of quantum mechanics, have the potential to break many of the encryption algorithms currently in use. Shor’s algorithm, for example, is a quantum algorithm that can factor large numbers exponentially faster than the best-known classical algorithms. While quantum computers are still in their early stages of development, their potential impact on cryptography is a major area of research and concern.
Additionally, there is growing interest in using machine learning and artificial intelligence to discover new patterns and relationships in number theory. AI algorithms can analyze vast amounts of data to identify potential factors and optimize factorization processes. These techniques could lead to breakthroughs in cryptography and other fields that rely on number theory.
From a professional standpoint, understanding factors and prime factorization is becoming increasingly important in various industries. Cryptographers, computer scientists, and engineers all need a solid foundation in number theory to develop secure systems and efficient algorithms. Moreover, educators are emphasizing the importance of teaching these concepts effectively to prepare students for future careers in STEM fields.
Tips and Expert Advice
One of the most effective tips for understanding factors is to use visual aids and real-world examples. For instance, you can use arrays of objects, such as marbles or blocks, to demonstrate how numbers can be divided into equal groups. This hands-on approach can make the concept of factors more concrete and easier to grasp. For example, to illustrate the factors of 8, you can arrange 8 marbles into different rectangular arrays: 1 row of 8 marbles, 2 rows of 4 marbles, 4 rows of 2 marbles, and 8 rows of 1 marble.
Another helpful tip is to practice regularly and start with smaller numbers. Begin by finding the factors of numbers like 6, 10, and 12 before moving on to larger numbers. This gradual approach helps build confidence and reinforces the fundamental concepts. You can also use online resources and interactive games to make learning more engaging.
When dealing with larger numbers, it's useful to know some basic divisibility rules. For example, a number is divisible by 2 if it ends in an even digit, by 3 if the sum of its digits is divisible by 3, by 5 if it ends in 0 or 5, and by 10 if it ends in 0. These rules can significantly speed up the process of finding factors and prime factorizations.
From an expert perspective, it's important to emphasize the connections between factors and other mathematical concepts. Factors are closely related to prime numbers, greatest common factors (GCF), and least common multiples (LCM). Understanding these relationships can provide a deeper understanding of number theory and its applications. For example, the GCF of two numbers is the largest factor that both numbers share, while the LCM is the smallest multiple that both numbers divide into evenly.
Consider the numbers 12 and 18. The factors of 12 are 1, 2, 3, 4, 6, and 12, while the factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors of 12 and 18 are 1, 2, 3, and 6. The greatest common factor (GCF) is 6, as it is the largest number that divides both 12 and 18 evenly.
The multiples of 12 are 12, 24, 36, 48, 60, and so on, while the multiples of 18 are 18, 36, 54, 72, 90, and so on. The least common multiple (LCM) is 36, as it is the smallest number that both 12 and 18 divide into evenly.
FAQ
Q: What exactly is a factor? A: A factor is a number that divides another number evenly, leaving no remainder. For example, 2 is a factor of 8 because 8 ÷ 2 = 4, with no remainder.
Q: How do I find the factors of a number? A: To find the factors of a number, you systematically divide the number by integers starting from 1 and check if the division results in a whole number. If it does, then the divisor is a factor.
Q: Are factors always positive? A: While factors are typically considered positive integers, negative integers can also be factors. For example, -2 is also a factor of 8 because 8 ÷ -2 = -4, with no remainder.
Q: What is the difference between a factor and a multiple? A: A factor divides a number evenly, whereas a multiple is the result of multiplying a number by an integer. For example, 2 is a factor of 8, while 16 is a multiple of 8.
Q: Why are factors important in mathematics? A: Factors are essential for simplifying fractions, finding common denominators, solving algebraic equations, and understanding number theory. They also have practical applications in various fields, including computer science and cryptography.
Conclusion
In summary, understanding which numbers are a factor of 8 involves identifying the numbers that divide 8 evenly, without leaving a remainder. These numbers include 1, 2, 4, and 8. The concept of factors is fundamental to many areas of mathematics and has practical applications in everyday life and various professional fields.
We encourage you to explore further and deepen your understanding of factors and related concepts. Try finding the factors of other numbers, such as 12, 15, or 24, to reinforce your knowledge. Share your findings or ask any questions in the comments below. Your active participation will help you master this essential mathematical concept and open doors to more advanced topics in number theory and beyond.
Latest Posts
Latest Posts
-
Angles In A Triangle Add Up To
Nov 17, 2025
-
What Are The 5 Spheres Of Earth
Nov 17, 2025
-
How To Find Difference Between Two Numbers In Excel
Nov 17, 2025
-
What Is A Biodiversity Hotspot Definition
Nov 17, 2025
-
Arrange Each Set Of Numbers In Increasing Order
Nov 17, 2025
Related Post
Thank you for visiting our website which covers about Which Number Is A Factor Of 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.