Whats The Lcm Of 8 And 12
catholicpriest
Nov 23, 2025 · 10 min read
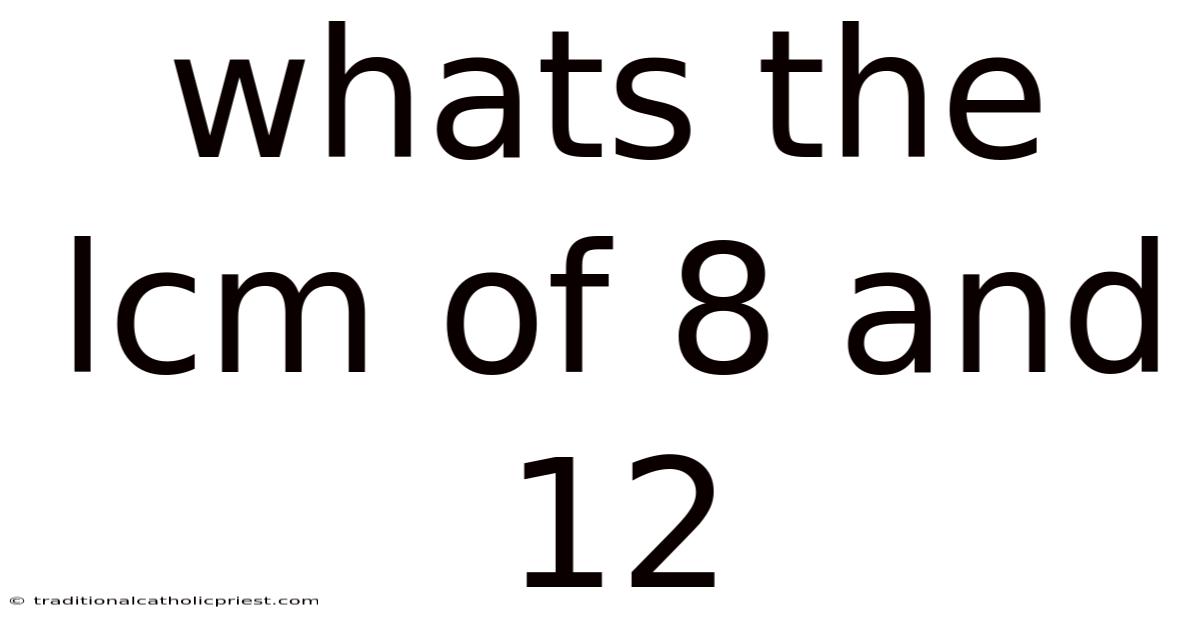
Table of Contents
Imagine you are organizing a party and want to buy an equal number of hot dogs and buns. Hot dogs come in packs of 8, while buns come in packs of 12. To avoid leftovers or shortages, you need to determine the smallest number of each that you can buy. This is a practical example of finding the least common multiple (LCM). The LCM of 8 and 12 is the smallest number that both 8 and 12 divide into evenly.
Understanding the LCM of 8 and 12 is more than just a mathematical exercise; it is a fundamental concept with applications in various real-world scenarios. From scheduling events to managing inventory, the LCM helps streamline processes and optimize resource allocation. In this article, we will explore the LCM in depth, covering its definition, methods for calculation, real-world applications, current trends, and expert advice.
Main Subheading
To fully grasp the LCM of 8 and 12, it’s essential to understand the context and background of this concept. The Least Common Multiple is a cornerstone of number theory, a branch of mathematics that deals with the properties and relationships of numbers. Understanding the LCM not only enhances mathematical proficiency but also provides valuable tools for solving practical problems.
The LCM is closely related to the Greatest Common Divisor (GCD), also known as the Highest Common Factor (HCF). While the LCM finds the smallest multiple shared by two or more numbers, the GCD identifies the largest factor that divides evenly into those numbers. These two concepts often work hand-in-hand in mathematical problem-solving and have numerous applications across different fields.
Comprehensive Overview
The Least Common Multiple (LCM) of two or more numbers is the smallest positive integer that is perfectly divisible by each of the numbers. In simpler terms, it is the smallest number that all the given numbers can divide into without leaving a remainder. For example, the LCM of 8 and 12 is 24 because 24 is the smallest number that both 8 and 12 divide into evenly.
The concept of LCM has deep historical roots, dating back to ancient civilizations that needed to solve problems related to time, measurement, and resource allocation. While the exact origins are difficult to pinpoint, early mathematicians recognized the importance of finding common multiples to simplify calculations and solve practical problems. Over time, different methods for calculating the LCM have been developed, each with its own advantages and applications.
Methods for Calculating the LCM
There are several methods for calculating the LCM of 8 and 12 or any set of numbers:
-
Listing Multiples:
- List the multiples of each number until you find a common multiple.
- Multiples of 8: 8, 16, 24, 32, 40, 48,...
- Multiples of 12: 12, 24, 36, 48, 60,...
- The smallest common multiple is 24.
-
Prime Factorization:
- Find the prime factorization of each number.
- 8 = 2^3
- 12 = 2^2 * 3
- Take the highest power of each prime factor that appears in either factorization.
- LCM = 2^3 * 3 = 8 * 3 = 24
-
Division Method:
-
Write the numbers in a row and divide by a common prime factor.
-
Continue until no common prime factor exists.
-
Multiply all the divisors and the remaining numbers to get the LCM.
-
Example:
2 | 8 12 2 | 4 6 2 | 2 3 3 | 1 3 | 1 1 -
LCM = 2 * 2 * 2 * 3 = 24
-
Mathematical Foundation
The mathematical foundation of the LCM lies in the properties of prime numbers and factorization. Every positive integer can be uniquely expressed as a product of prime numbers raised to certain powers. This is known as the Fundamental Theorem of Arithmetic. By breaking down numbers into their prime factors, we can easily identify the common and unique factors needed to compute the LCM.
The formula that relates the LCM and the Greatest Common Divisor (GCD) is:
LCM(a, b) * GCD(a, b) = |a * b|
Where:
- LCM(a, b) is the least common multiple of a and b.
- GCD(a, b) is the greatest common divisor of a and b.
- |a * b| is the absolute value of the product of a and b.
Using this formula, we can find the LCM of 8 and 12 if we know their GCD. The GCD of 8 and 12 is 4.
LCM(8, 12) = (8 * 12) / GCD(8, 12) = (8 * 12) / 4 = 96 / 4 = 24
Importance of Understanding LCM
Understanding the LCM of 8 and 12 and the broader concept is crucial for several reasons:
- Simplifying Fractions: When adding or subtracting fractions with different denominators, finding the LCM of the denominators allows you to rewrite the fractions with a common denominator, making the operation easier.
- Solving Algebraic Equations: The LCM is often used to clear fractions in algebraic equations, simplifying the equation and making it easier to solve.
- Scheduling and Planning: As illustrated in the opening example, the LCM is useful in scheduling events or tasks that occur at regular intervals.
- Resource Allocation: In business and logistics, the LCM can help optimize resource allocation by finding the smallest quantity that satisfies multiple requirements.
Practical Examples
To further illustrate the importance of the LCM of 8 and 12, let's consider a few practical examples:
- Scheduling: Suppose you have two tasks, one that needs to be done every 8 days and another that needs to be done every 12 days. To find out when both tasks will occur on the same day, you need to find the LCM of 8 and 12, which is 24. Therefore, both tasks will occur together every 24 days.
- Manufacturing: A factory produces two types of items. Item A requires 8 minutes on a machine, and Item B requires 12 minutes. To schedule production efficiently, the manager needs to know the shortest time interval after which both items can be produced simultaneously. Again, the LCM of 8 and 12 is essential here.
- Purchasing: As mentioned in the introduction, if hot dogs come in packs of 8 and buns in packs of 12, the LCM of 8 and 12 (which is 24) tells you that you need to buy 3 packs of hot dogs and 2 packs of buns to have an equal number of each.
Trends and Latest Developments
In recent years, the use of LCM in various fields has been enhanced by technological advancements and data-driven approaches. Here are some trends and latest developments:
- Algorithmic Optimization: Computer algorithms now use LCM to optimize complex scheduling and resource allocation problems. These algorithms can handle much larger datasets and more variables than traditional manual methods.
- Financial Modeling: In finance, the LCM is used in modeling cyclical patterns and predicting future trends. For example, analysts may use the LCM to align different investment cycles or to forecast market fluctuations.
- Supply Chain Management: Modern supply chain management systems use LCM to synchronize different processes and ensure timely delivery of goods. This helps reduce inventory costs and improve overall efficiency.
- Educational Tools: There has been an increase in interactive educational tools that help students understand the concept of LCM. These tools often use visual aids and gamification to make learning more engaging.
The popular opinion among mathematicians and educators is that a strong understanding of basic concepts like LCM is crucial for success in more advanced mathematical studies. Many believe that early exposure to these concepts helps develop critical thinking and problem-solving skills.
Tips and Expert Advice
To master the LCM of 8 and 12 and its applications, consider the following tips and expert advice:
- Practice Regularly: The best way to become proficient in calculating the LCM is to practice regularly. Work through different examples and try different methods to find the one that works best for you.
- Understand the Underlying Concepts: Don't just memorize the steps for calculating the LCM. Make sure you understand the underlying mathematical concepts, such as prime factorization and divisibility.
- Use Real-World Examples: Relate the concept of LCM to real-world examples. This will help you understand its practical applications and make it easier to remember.
- Utilize Online Resources: Take advantage of the many online resources available, such as tutorials, practice problems, and interactive tools. These resources can provide additional support and help you learn at your own pace.
- Seek Help When Needed: Don't be afraid to ask for help if you're struggling with the concept of LCM. Talk to a teacher, tutor, or classmate who can provide guidance and clarification.
Expert Insights
Experts in mathematics education emphasize the importance of teaching LCM in a way that is both engaging and relevant. They recommend using visual aids, hands-on activities, and real-world examples to help students understand the concept. Additionally, they suggest focusing on problem-solving skills rather than rote memorization.
For example, consider this problem:
A baker wants to make identical cupcakes for a party. She can bake cupcakes in batches of 8 chocolate cupcakes or 12 vanilla cupcakes. What is the smallest number of each type of cupcake she can bake so that she has the same number of chocolate and vanilla cupcakes?
To solve this problem, students need to recognize that they need to find the LCM of 8 and 12. By applying the methods discussed earlier, they can determine that the LCM is 24. Therefore, the baker needs to bake 3 batches of chocolate cupcakes and 2 batches of vanilla cupcakes to have 24 of each type.
Additional Tips
Here are some additional tips for mastering the LCM:
- Use Flashcards: Create flashcards with different pairs of numbers and practice finding their LCM.
- Join a Study Group: Collaborate with classmates to study and solve problems together.
- Watch Online Tutorials: There are many excellent online tutorials that explain the concept of LCM in detail.
- Practice with Word Problems: Word problems can help you apply your knowledge of LCM to real-world scenarios.
- Review Regularly: Review the concept of LCM regularly to reinforce your understanding.
FAQ
Q: What is the LCM?
A: The Least Common Multiple (LCM) of two or more numbers is the smallest positive integer that is perfectly divisible by each of the numbers.
Q: How do you find the LCM of 8 and 12?
A: You can find the LCM of 8 and 12 by listing multiples, using prime factorization, or the division method. The LCM is 24.
Q: Why is understanding LCM important?
A: Understanding LCM is important for simplifying fractions, solving algebraic equations, scheduling, and resource allocation.
Q: Can the LCM be larger than the numbers?
A: Yes, the LCM is usually larger than the numbers, unless one number is a multiple of the other.
Q: What is the relationship between LCM and GCD?
A: The relationship is: LCM(a, b) * GCD(a, b) = |a * b|.
Conclusion
In summary, the LCM of 8 and 12 is 24, and understanding how to calculate the LCM is crucial for various applications in mathematics and real-world scenarios. From scheduling events to optimizing resource allocation, the LCM helps simplify complex problems and improve efficiency. By mastering the methods for calculating the LCM and understanding its underlying concepts, you can enhance your mathematical proficiency and problem-solving skills.
Now that you have a comprehensive understanding of the LCM, take the next step by practicing with different examples and exploring its applications in your own life. Share this article with others who might benefit from learning about the LCM, and don't hesitate to ask questions or seek further clarification if needed. Happy calculating!
Latest Posts
Latest Posts
-
What Is The Difference Between A Verb And Adverb
Nov 23, 2025
-
What Are Lines Of Symmetry In Math
Nov 23, 2025
-
What Is A Current Account Economics
Nov 23, 2025
-
Geometry Basics Points Lines And Planes
Nov 23, 2025
-
Which Elements Are Considered Noble Metals
Nov 23, 2025
Related Post
Thank you for visiting our website which covers about Whats The Lcm Of 8 And 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.