What Is The Lcm Of 9 And 12
catholicpriest
Nov 22, 2025 · 13 min read
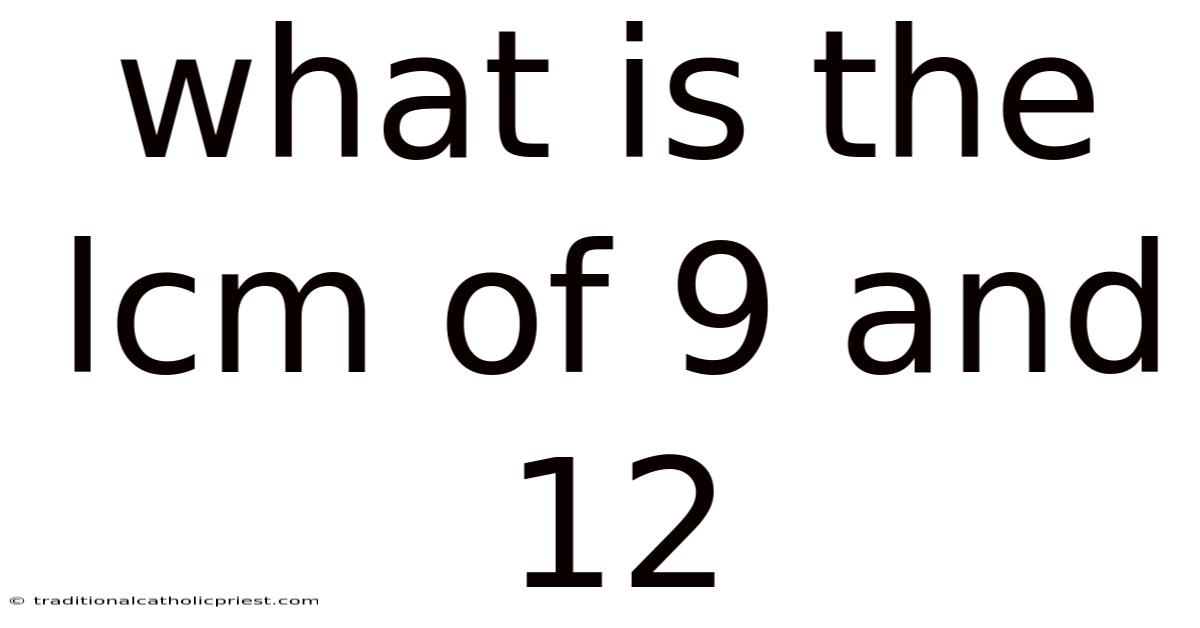
Table of Contents
Imagine you are planning a party and want to buy both hot dogs and buns. The hot dogs come in packs of 9, and the buns come in packs of 12. You want to buy the exact same number of hot dogs and buns, without any leftovers. How many packs of each do you need to buy? This puzzle, seemingly simple, leads us to the heart of a fundamental concept in mathematics: the Least Common Multiple, or LCM. Finding the LCM of numbers like 9 and 12 is not just an academic exercise; it's a practical skill with applications in various real-world scenarios, from scheduling events to designing gears.
The Least Common Multiple (LCM) is the smallest positive integer that is evenly divisible by two or more numbers. In simpler terms, it's the smallest number that both (or all) of the given numbers can divide into without leaving a remainder. The LCM of 9 and 12 specifically, is the smallest number that both 9 and 12 divide into cleanly. This concept is incredibly useful in simplifying fractions, solving algebraic equations, and, as we've seen, tackling everyday problems that involve finding common ground. Let's delve deeper into understanding what the LCM is, why it matters, and how to calculate it effectively.
Main Subheading
To truly grasp the LCM of 9 and 12, or any set of numbers, it's essential to understand the broader context of multiples, common multiples, and the very concept of "least." Multiples are the numbers you get when you multiply a given number by an integer. For example, the multiples of 9 are 9, 18, 27, 36, 45, and so on, while the multiples of 12 are 12, 24, 36, 48, 60, and so on. Common multiples are the numbers that appear in the lists of multiples for two or more numbers. In our case, 36 is a common multiple of both 9 and 12, as are 72, 108, and so on.
However, the LCM is not just any common multiple; it's the smallest one. This "least" aspect is crucial. While identifying common multiples is a good start, the LCM provides the most efficient and practical solution in many situations. Think back to our hot dog and bun scenario: While buying 72 of each would certainly work, buying only 36 minimizes waste and expense. Understanding this foundational principle sets the stage for exploring various methods of calculating the LCM and appreciating its significance in different mathematical and real-world contexts.
Comprehensive Overview
The LCM of 9 and 12 is a fundamental concept in number theory that helps simplify many mathematical problems. At its core, the LCM provides a way to find the smallest number that two or more integers can divide into without leaving a remainder. This has implications far beyond simple arithmetic.
Definition and Mathematical Foundation
The Least Common Multiple (LCM) of two or more integers is the smallest positive integer that is a multiple of all the given integers. Mathematically, if we have two integers, a and b, their LCM, denoted as LCM(a, b), satisfies the following conditions:
- LCM(a, b) is a multiple of a.
- LCM(a, b) is a multiple of b.
- LCM(a, b) is the smallest positive integer satisfying conditions 1 and 2.
This definition is rooted in the basic principles of divisibility and multiples in number theory. It connects to other important concepts like the Greatest Common Divisor (GCD), as the LCM and GCD of two numbers are related by the formula:
LCM(a, b) = (a * b) / GCD(a, b)
Historical Context
The concept of multiples and common multiples has been around since the early days of mathematics. Ancient civilizations needed ways to divide resources, schedule events, and measure quantities. Though they may not have formally defined the "Least Common Multiple" in the way we do today, the underlying idea was certainly present. For example, early astronomers needed to find common cycles in celestial events, which is essentially a problem of finding the LCM of different periods. The formalization of number theory concepts like LCM came later, with significant contributions from Greek mathematicians like Euclid, who provided algorithms for finding the GCD, which indirectly helps in finding the LCM.
Methods for Calculating the LCM
There are several methods to calculate the LCM of 9 and 12, each with its own advantages and suitability depending on the numbers involved:
-
Listing Multiples: This involves listing the multiples of each number until a common multiple is found. As mentioned earlier, list the multiples of 9 (9, 18, 27, 36, 45, ...) and the multiples of 12 (12, 24, 36, 48, ...). The smallest common multiple is 36, so the LCM of 9 and 12 is 36.
-
Prime Factorization: This method involves breaking down each number into its prime factors. Then, for each prime factor, take the highest power that appears in any of the factorizations and multiply them together.
- Prime factorization of 9: 3^2
- Prime factorization of 12: 2^2 * 3
The LCM is then 2^2 * 3^2 = 4 * 9 = 36.
-
Using the GCD: As mentioned earlier, LCM(a, b) = (a * b) / GCD(a, b). To find the LCM of 9 and 12 using this method, first find the GCD of 9 and 12, which is 3. Then, LCM(9, 12) = (9 * 12) / 3 = 108 / 3 = 36.
Practical Applications of LCM
The LCM isn't just a theoretical concept; it has many practical applications:
-
Scheduling: If you have two events that occur at different intervals, the LCM can help you determine when they will occur at the same time. For example, if one event happens every 9 days and another every 12 days, they will both occur on the same day every 36 days (the LCM of 9 and 12).
-
Fractions: The LCM is used to find the least common denominator when adding or subtracting fractions. This simplifies the process and makes calculations easier.
-
Gear Ratios: In mechanical engineering, the LCM is used to calculate gear ratios. If two gears have 9 and 12 teeth respectively, the LCM helps determine how many rotations each gear must make before they return to their starting positions relative to each other.
-
Real-world scenarios: As we demonstrated earlier, LCM can also be used for party planning, such as buying hot dogs and buns, where you want to ensure an equal number of each.
Why Understanding LCM is Important
Understanding the LCM is crucial for several reasons:
-
Problem Solving: It provides a systematic way to solve problems involving multiples and divisibility.
-
Mathematical Foundation: It is a building block for more advanced mathematical concepts.
-
Efficiency: It helps simplify calculations and find the most efficient solutions in various real-world scenarios.
The LCM of 9 and 12, being 36, is a prime example of how this concept works. By understanding the definition, methods, and applications of the LCM, one can appreciate its importance in both theoretical and practical contexts.
Trends and Latest Developments
While the fundamental concept of the LCM of 9 and 12 remains constant, its application and the tools used to calculate it have evolved with technological advancements. The trends and latest developments in this area are primarily focused on computational efficiency and integration with modern software and programming.
Computational Tools and Software
Today, calculating the LCM is rarely done manually for large numbers. Instead, various computational tools and software packages are used:
-
Online Calculators: Numerous websites offer LCM calculators that can quickly compute the LCM of any set of numbers. These tools are easily accessible and often free.
-
Programming Languages: Most programming languages (e.g., Python, Java, C++) have built-in functions or libraries to calculate the LCM. For example, in Python, you can use the
math.lcm()function (introduced in Python 3.9) or implement a custom function using the GCD. -
Spreadsheet Software: Programs like Microsoft Excel and Google Sheets have functions to calculate the GCD, which can then be used to find the LCM using the formula LCM(a, b) = (a * b) / GCD(a, b).
Integration with Educational Platforms
Educational platforms are increasingly incorporating interactive tools and visualizations to help students understand the LCM concept. These tools often include:
-
Interactive Tutorials: Step-by-step guides that walk students through the process of finding the LCM using different methods.
-
Visual Aids: Diagrams and animations that illustrate the concept of multiples and common multiples.
-
Practice Problems: Automatically generated problems with instant feedback to help students master the LCM.
Data Analysis and LCM
In data analysis, the LCM can be used in scenarios involving periodic events or cycles. For instance, in time series analysis, if you have data that repeats at different intervals, the LCM can help you align the data for comparison. Suppose you have sales data that peaks every 9 months due to one seasonal factor and every 12 months due to another. Using the LCM of 9 and 12 (which is 36) would allow you to predict when both seasonal factors will align, leading to a significant peak in sales every 36 months.
Professional Insights
From a professional perspective, understanding the LCM is essential for:
-
Software Developers: When designing algorithms that involve scheduling or synchronization, the LCM can be a valuable tool.
-
Engineers: In mechanical and electrical engineering, the LCM is used in designing gear systems, electrical circuits, and other systems involving periodic phenomena.
-
Financial Analysts: As mentioned earlier, in financial modeling, understanding cyclic patterns and aligning data using the LCM can provide valuable insights.
The latest developments in LCM calculation and application focus on leveraging technology to improve efficiency and accessibility. While the core concept remains the same, the tools and techniques used to apply it are constantly evolving.
Tips and Expert Advice
Mastering the concept of the LCM of 9 and 12 or any set of numbers goes beyond just knowing the definition and calculation methods. Here are some tips and expert advice to enhance your understanding and application of the LCM:
Tip 1: Understand the Relationship Between LCM and GCD
The Greatest Common Divisor (GCD) and Least Common Multiple (LCM) are closely related. Understanding this relationship can simplify calculations and provide deeper insights. The formula LCM(a, b) = (a * b) / GCD(a, b) is a powerful tool.
- Example: Let's say you need to find the LCM of 24 and 36. First, find the GCD of 24 and 36, which is 12. Then, use the formula: LCM(24, 36) = (24 * 36) / 12 = 864 / 12 = 72. This approach can be particularly useful when dealing with larger numbers where listing multiples might be cumbersome. Knowing this relationship allows you to choose the most efficient method based on the given numbers.
Tip 2: Use Prime Factorization for Complex Numbers
When dealing with more than two numbers or when the numbers are large and composite, prime factorization is often the most efficient method for finding the LCM.
-
Example: Find the LCM of 18, 24, and 30.
- Prime factorization of 18: 2 * 3^2
- Prime factorization of 24: 2^3 * 3
- Prime factorization of 30: 2 * 3 * 5
- LCM(18, 24, 30) = 2^3 * 3^2 * 5 = 8 * 9 * 5 = 360
This method ensures that you account for all prime factors and their highest powers, guaranteeing the smallest common multiple. Prime factorization breaks down the problem into smaller, more manageable parts, making it easier to solve complex LCM problems.
Tip 3: Look for Patterns and Simplifications
Sometimes, you can simplify the process by recognizing patterns or relationships between the numbers. For example, if one number is a multiple of another, the LCM is simply the larger number.
- Example: Find the LCM of 7 and 21. Since 21 is a multiple of 7, the LCM(7, 21) is 21. Recognizing these patterns can save time and effort. Another pattern to look for is when numbers are relatively prime (i.e., their GCD is 1). In such cases, the LCM is simply the product of the numbers. For example, the LCM of 8 and 9 is 8 * 9 = 72 because their GCD is 1.
Tip 4: Practice with Real-World Problems
The best way to master the LCM is to practice applying it to real-world problems. This not only reinforces your understanding but also helps you appreciate the practical relevance of the concept.
- Example: Consider a scenario where you are organizing a sports event. One activity occurs every 6 days, and another occurs every 8 days. You want to know when both activities will occur on the same day. This is an LCM problem. The LCM of 6 and 8 is 24, so both activities will occur together every 24 days. Applying the LCM to practical situations makes the concept more tangible and easier to remember.
Tip 5: Use Technology Wisely
While technology can be a great tool for calculating the LCM, it's important to understand the underlying concepts. Don't rely solely on calculators without understanding how the LCM is derived.
- Example: Use online calculators or programming tools to check your work and handle complex calculations, but always try to solve the problem manually first. This helps reinforce your understanding and builds your problem-solving skills. Technology should augment your understanding, not replace it.
By following these tips and practicing regularly, you can develop a solid understanding of the LCM and its applications. The LCM of 9 and 12 serves as a simple yet powerful example of how this concept can be used to solve practical problems.
FAQ
Q: What is the LCM?
A: The Least Common Multiple (LCM) is the smallest positive integer that is a multiple of two or more numbers.
Q: How do you find the LCM of 9 and 12?
A: There are several methods: listing multiples, prime factorization, or using the GCD. The LCM of 9 and 12 is 36.
Q: Why is the LCM important?
A: The LCM is important for simplifying fractions, solving algebraic equations, scheduling events, and various other real-world applications.
Q: Can the LCM be larger than the numbers you are finding the LCM of?
A: Yes, the LCM is typically larger than or equal to the largest number in the set. It is only smaller if one number is a multiple of the other, in which case, the LCM is the larger number.
Q: What is the relationship between LCM and GCD?
A: The LCM and GCD are related by the formula: LCM(a, b) = (a * b) / GCD(a, b). Understanding this relationship can simplify LCM calculations.
Q: Is there an LCM for more than two numbers?
A: Yes, the LCM can be found for any number of integers. The same methods (listing multiples, prime factorization) can be extended to find the LCM of multiple numbers.
Conclusion
Understanding the LCM of 9 and 12 and the broader concept of Least Common Multiples is more than just an academic exercise; it's a practical skill with wide-ranging applications. From scheduling events and simplifying fractions to solving complex engineering problems, the LCM provides a systematic way to find common ground and optimize solutions. By mastering the various methods of calculating the LCM, such as listing multiples, prime factorization, and using the GCD, you equip yourself with a valuable tool for problem-solving in both mathematical and real-world contexts.
Now that you have a comprehensive understanding of the LCM, it's time to put your knowledge to the test. Try solving some practice problems and exploring real-world scenarios where the LCM can be applied. Share your findings and any interesting applications you discover in the comments below. Let's continue the discussion and deepen our understanding of this fascinating mathematical concept together!
Latest Posts
Latest Posts
-
Area Of A Square With Different Lengths
Nov 22, 2025
-
Ending A Sentence With To Be
Nov 22, 2025
-
What Are The Properties Of A Gas
Nov 22, 2025
-
What Are The 4 Main Stages Of The Water Cycle
Nov 22, 2025
-
Do Mitochondria Have Their Own Ribosomes
Nov 22, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 9 And 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.