What Is The Derivative Of Sin X 2
catholicpriest
Nov 25, 2025 · 12 min read
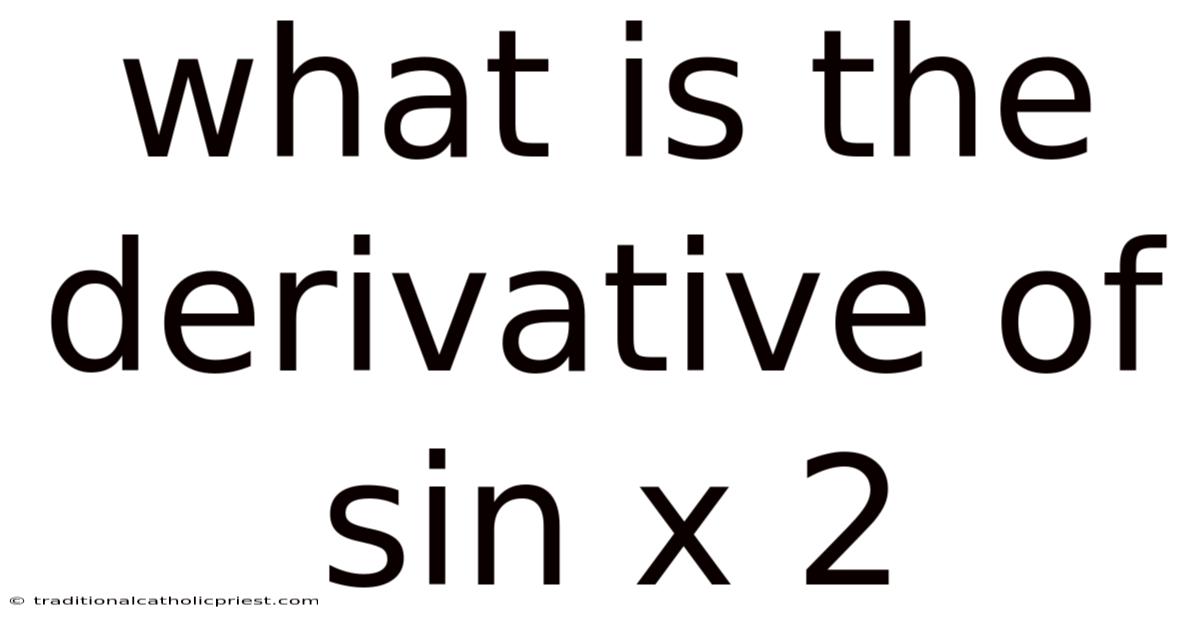
Table of Contents
Imagine you're on a roller coaster, soaring up and down a series of hills. At any given moment, you're either climbing, descending, or momentarily at the peak or valley. The derivative of a function, especially something like sin x², is like knowing your exact rate of ascent or descent at every single point on that roller coaster ride. It tells you how dramatically things are changing at any instant.
Understanding derivatives isn't just about math; it's about understanding change itself. From predicting stock market fluctuations to optimizing engineering designs, derivatives play a crucial role in many fields. The derivative of sin x² may seem abstract, but it’s a fundamental concept with practical applications that touch our daily lives in ways we might not even realize. Let's dive in and unravel the mysteries behind this important mathematical concept.
Main Subheading
To really understand what the derivative of sin x² is, we need to break it down into its components and apply some fundamental calculus principles. Derivatives, at their core, measure the instantaneous rate of change of a function. Think of it as zooming in infinitely close to a curve until it looks like a straight line. The slope of that line is the derivative at that point.
In the case of sin x², we are dealing with a composite function, meaning a function within a function. Specifically, we have the sine function applied to x², or sin(x²). To find its derivative, we need to use the chain rule, a powerful tool in calculus for differentiating composite functions. The chain rule essentially says that the derivative of a composite function is the derivative of the outer function (evaluated at the inner function) multiplied by the derivative of the inner function. This process might seem a bit abstract now, but we will break it down step by step to make it clear.
Comprehensive Overview
What is a Derivative?
At its core, a derivative represents the instantaneous rate of change of a function with respect to one of its variables. In simpler terms, it measures how much a function's output changes when there is a very small change in its input. Graphically, the derivative at a point on a curve is the slope of the tangent line at that point.
The concept of a derivative is fundamental to calculus and has its roots in the problem of finding tangent lines to curves. Historically, mathematicians like Isaac Newton and Gottfried Wilhelm Leibniz independently developed calculus in the 17th century. Newton approached it from a physics perspective, focusing on rates of change and motion, while Leibniz emphasized the mathematical formalism and notation that we still use today.
The formal definition of the derivative involves limits. The derivative of a function f(x) at a point x is defined as:
f'(x) = lim (h -> 0) [f(x + h) - f(x)] / h
This limit represents the slope of the secant line between two points on the curve of f(x) as the distance h between those points approaches zero, thus giving us the slope of the tangent line.
Understanding sin x²
Before we find the derivative of sin x², let’s clarify what sin x² means. It represents the sine function applied to the square of x. In mathematical notation:
f(x) = sin(x²)
Here, x² is the inner function and sin(u) is the outer function, where u = x². This composition is crucial because it dictates how we apply the chain rule.
The sine function itself, sin(x), oscillates between -1 and 1 as x varies. When we input x² into the sine function, the behavior changes. Because x² grows more rapidly than x, the oscillations of sin(x²) become more frequent as x moves away from zero. This increased frequency affects the derivative, making it more complex than the derivative of simple sin(x).
The Chain Rule Explained
The chain rule is a fundamental concept in calculus that allows us to find the derivative of composite functions. A composite function is a function that is composed of another function; in other words, it's a function inside another function. Mathematically, if we have a function y = f(g(x)), then the chain rule states:
dy/dx = dy/du * du/dx
Where u = g(x). In simpler terms, the derivative of the composite function is the derivative of the outer function (evaluated at the inner function) multiplied by the derivative of the inner function.
To illustrate, consider y = sin(x²). Here, the outer function f(u) = sin(u) and the inner function g(x) = x². Applying the chain rule, we first find the derivative of the outer function with respect to u, which is cos(u). Then, we find the derivative of the inner function with respect to x, which is 2x. Multiplying these together gives us the derivative of the entire composite function:
dy/dx = cos(u) * 2x = cos(x²) * 2x
Thus, the derivative of sin(x²) is 2x * cos(x²).
Step-by-Step Differentiation of sin x²
Now, let's go through the differentiation of sin x² step by step to solidify our understanding.
-
Identify the Outer and Inner Functions:
- Outer function: f(u) = sin(u)
- Inner function: g(x) = x²
-
Find the Derivative of the Outer Function:
- The derivative of sin(u) with respect to u is cos(u).
- So, f'(u) = cos(u).
-
Find the Derivative of the Inner Function:
- The derivative of x² with respect to x is 2x.
- So, g'(x) = 2x.
-
Apply the Chain Rule:
- dy/dx = f'(g(x)) * g'(x)
- Substitute g(x) = x² into f'(u): f'(x²) = cos(x²)
- Multiply by the derivative of the inner function: dy/dx = cos(x²) * 2x
Therefore, the derivative of sin x² is 2x * cos x².
Importance of Understanding Composite Functions
Understanding composite functions is crucial because they appear frequently in various mathematical and real-world contexts. Recognizing how functions are composed allows for a structured approach to differentiation, which is essential for problem-solving in calculus and related fields.
Moreover, mastering composite functions and the chain rule builds a strong foundation for more advanced calculus topics, such as implicit differentiation, related rates, and multivariable calculus. These concepts are vital for modeling complex systems and solving intricate problems in physics, engineering, economics, and computer science.
Trends and Latest Developments
In recent years, the application of derivatives has expanded significantly, driven by advancements in computational power and the increasing complexity of mathematical models used in various fields. One notable trend is the use of derivatives in machine learning, particularly in training neural networks.
Machine Learning and Optimization: Neural networks are trained using optimization algorithms that rely heavily on derivatives. The backpropagation algorithm, which is used to adjust the weights of the network based on the error in its predictions, utilizes the chain rule to compute gradients of the loss function with respect to the network's parameters. This allows the network to learn and improve its performance over time. Complex functions that are used in neural networks often involve compositions of various functions, making the chain rule and understanding composite functions essential for training these models.
Financial Modeling: Derivatives play a crucial role in financial modeling, particularly in pricing options and other derivative securities. The Black-Scholes model, a widely used model for option pricing, relies on calculus and derivatives to estimate the fair value of an option based on factors such as the underlying asset's price, volatility, and time to expiration.
Physics and Engineering: In physics and engineering, derivatives are used extensively to model motion, forces, and other dynamic systems. For example, in mechanics, derivatives are used to calculate velocity (the rate of change of position) and acceleration (the rate of change of velocity). In electrical engineering, derivatives are used to analyze circuits and model the behavior of electrical components.
Professional Insights: The increasing reliance on data-driven models has further emphasized the importance of derivatives. As models become more complex, understanding the underlying mathematical principles, including derivatives and the chain rule, is essential for ensuring the accuracy and reliability of these models. Professionals in fields such as data science, finance, and engineering need a strong foundation in calculus to effectively apply these models and interpret their results. Moreover, the development of new optimization algorithms and techniques requires a deep understanding of derivatives and their properties.
Tips and Expert Advice
When tackling derivatives, especially of composite functions like sin x², there are several strategies and insights that can help simplify the process and improve accuracy.
Tip 1: Master the Basic Derivatives:
Before attempting to differentiate complex functions, ensure you have a solid understanding of the derivatives of basic functions such as polynomials, trigonometric functions, exponential functions, and logarithmic functions. Knowing that the derivative of sin(x) is cos(x) and the derivative of x² is 2x is foundational for applying the chain rule effectively.
For instance, practice differentiating simple functions like x³, cos(x), e^x, and ln(x) until you can quickly recall their derivatives. This will make it easier to recognize and apply the chain rule when you encounter more complex functions.
Tip 2: Practice Identifying Outer and Inner Functions:
The key to applying the chain rule successfully is to correctly identify the outer and inner functions in a composite function. Practice breaking down complex functions into their component parts. For example, in sin(e^x), the outer function is sin(u) and the inner function is e^x. Similarly, in √(x² + 1), the outer function is √u and the inner function is x² + 1.
By practicing this decomposition, you will become more adept at recognizing the structure of composite functions and applying the chain rule correctly. Start with simpler examples and gradually work your way up to more complex ones.
Tip 3: Write Out Each Step Clearly:
When applying the chain rule, it's helpful to write out each step clearly to avoid errors. Start by identifying the outer and inner functions, then find their derivatives separately, and finally, apply the chain rule formula. This structured approach can help you stay organized and reduce the likelihood of making mistakes.
For example, when differentiating sin(x²), write out:
- Outer function: f(u) = sin(u), f'(u) = cos(u)
- Inner function: g(x) = x², g'(x) = 2x
- Chain rule: dy/dx = f'(g(x)) * g'(x) = cos(x²) * 2x = 2x * cos(x²)
Tip 4: Use Substitution to Simplify:
In some cases, using substitution can make it easier to differentiate composite functions. Let u be the inner function, and then differentiate the outer function with respect to u. After that, substitute the original inner function back into the result and multiply by the derivative of the inner function with respect to x.
For example, when differentiating cos(5x), let u = 5x. Then, the function becomes cos(u), and its derivative with respect to u is -sin(u). Now, substitute back u = 5x and multiply by the derivative of 5x with respect to x, which is 5. The result is -5sin(5x).
Tip 5: Check Your Work:
After differentiating a function, always check your work to ensure that you haven't made any mistakes. One way to do this is to use online derivative calculators to verify your answer. Another approach is to use numerical methods to approximate the derivative at a few points and compare the results with your calculated derivative.
Additionally, practice differentiating a variety of functions to build your skills and confidence. The more you practice, the better you will become at recognizing patterns and applying the appropriate differentiation techniques.
FAQ
Q: What is the chain rule and why is it important?
A: The chain rule is a fundamental concept in calculus used to find the derivative of composite functions. It states that the derivative of a composite function is the derivative of the outer function (evaluated at the inner function) multiplied by the derivative of the inner function. It's important because many functions we encounter in math and real-world applications are composite.
Q: Can the chain rule be applied multiple times in a single problem?
A: Yes, the chain rule can be applied multiple times if you have nested composite functions. For example, if you have f(g(h(x))), you would apply the chain rule iteratively, working from the outermost function inward.
Q: What is the derivative of sin(x)?
A: The derivative of sin(x) with respect to x is cos(x). This is a basic derivative that is essential to know for differentiating trigonometric functions.
Q: How does the derivative of sin x² differ from the derivative of sin²x?
A: sin x² means sin(x²), while sin²x means (sin x)². For sin x², you apply the chain rule once. For sin²x, you also use the chain rule, but the outer function is u² and the inner function is sin x. The derivative of sin x² is 2x*cos(x²), while the derivative of sin²x is 2sin(x)cos(x).
Q: What are some real-world applications of derivatives?
A: Derivatives have numerous real-world applications, including:
- Physics: Calculating velocity and acceleration.
- Engineering: Optimizing designs and analyzing systems.
- Economics: Modeling economic growth and predicting market trends.
- Computer Science: Training machine learning models and optimizing algorithms.
Conclusion
Understanding the derivative of sin x² involves grasping the core principles of calculus, particularly the chain rule, and how it applies to composite functions. We've explored the definition of derivatives, delved into the step-by-step process of differentiating sin x², discussed current trends in the application of derivatives, and provided expert tips to improve your differentiation skills.
Mastering these concepts not only enhances your mathematical abilities but also opens doors to a wide range of practical applications in various fields. Whether you're a student, an engineer, a data scientist, or simply a curious learner, a solid understanding of derivatives is invaluable.
Now that you have a comprehensive understanding of the derivative of sin x², take the next step by practicing more examples, exploring advanced calculus topics, and applying your knowledge to real-world problems. Share this article with your friends and colleagues, and leave a comment below to let us know how this guide has helped you. What other calculus topics would you like us to cover in the future?
Latest Posts
Latest Posts
-
Life Cycle Of A Bee For Kids
Nov 25, 2025
-
Whole Number And Fraction To Decimal
Nov 25, 2025
-
What Tool Is Used To Measure Atmospheric Pressure
Nov 25, 2025
-
Fine Grained Vs Coarse Grained Rocks
Nov 25, 2025
-
How To Find Lines That Are Perpendicular
Nov 25, 2025
Related Post
Thank you for visiting our website which covers about What Is The Derivative Of Sin X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.