What Is Half Of 47 And 1 4
catholicpriest
Nov 16, 2025 · 9 min read
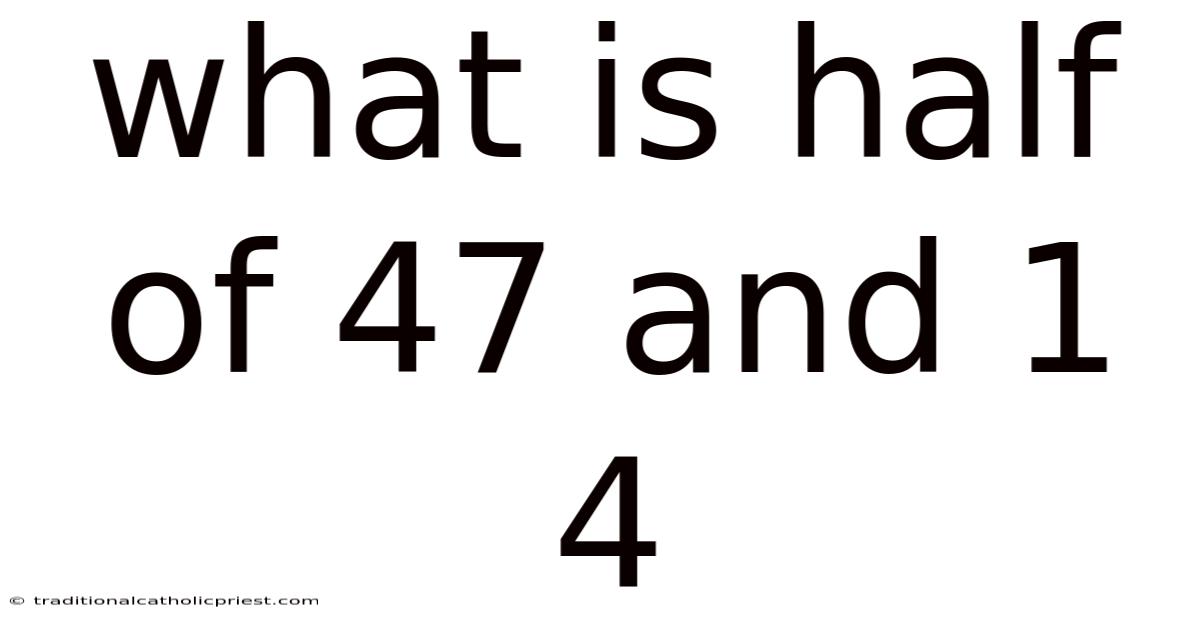
Table of Contents
The question "what is half of 47 and 1/4" might seem straightforward at first glance, but it involves a bit of mathematical finesse to ensure accuracy. Many people quickly jump to dividing 47 by two, but the presence of the fraction 1/4 adds a layer of complexity that requires careful consideration. This article delves deep into understanding how to accurately calculate half of 47 and 1/4, providing a comprehensive guide suitable for anyone looking to improve their arithmetic skills.
Main Subheading: Understanding the Question
Before diving into calculations, it's crucial to understand exactly what the question is asking. The phrase "half of 47 and 1/4" implies we need to find half of the combined value of 47 and 1/4. This means we must first add 47 and 1/4 together and then divide the result by 2. A clear understanding of this order of operations is essential to avoid errors. Let's break down the components: we have a whole number (47) and a fraction (1/4). Combining these into a single number will set us up for finding half of the total value. Ignoring the fractional part or misinterpreting the order will lead to an incorrect answer. Thus, precision and attention to detail are paramount.
Comprehensive Overview
What is a Fraction?
A fraction represents a part of a whole. It is written as one number over another, separated by a line. The number above the line is the numerator, which indicates how many parts we have. The number below the line is the denominator, which indicates how many equal parts the whole is divided into. For example, in the fraction 1/4, the numerator is 1, and the denominator is 4. This means we have one part out of four equal parts. Fractions are fundamental in mathematics, representing quantities that are not whole numbers. Understanding fractions is crucial for performing arithmetic operations accurately.
Converting Mixed Numbers
A mixed number is a combination of a whole number and a fraction, such as 47 and 1/4. To perform calculations easily, it's often useful to convert a mixed number into an improper fraction. An improper fraction is one where the numerator is greater than or equal to the denominator. To convert 47 and 1/4 into an improper fraction, we multiply the whole number (47) by the denominator (4) and then add the numerator (1). This result becomes the new numerator, and we keep the original denominator. So, (47 * 4) + 1 = 188 + 1 = 189. Therefore, 47 and 1/4 is equivalent to 189/4 as an improper fraction.
Dividing by Two
Dividing by two is the same as finding half of a number. It's a basic arithmetic operation that can be performed on both whole numbers and fractions. For whole numbers, we simply divide the number by 2. For fractions, dividing by two can be done by either dividing the numerator by 2 (if it's an even number) or multiplying the denominator by 2. The latter approach is generally more straightforward, especially when the numerator is odd.
The Concept of "and" in Mathematics
In mathematical contexts, the word "and" often implies addition. When you see "47 and 1/4," it means you should add 47 and 1/4 together to find their combined value. This is a common convention in arithmetic, and recognizing it is essential for correctly interpreting mathematical expressions. Failing to recognize "and" as an indicator of addition can lead to misinterpretations and incorrect calculations.
Why Precision Matters
In mathematics, precision is crucial. Even small errors can lead to significantly different results. When dealing with fractions and mixed numbers, it's especially important to be precise in each step of the calculation. This includes correctly converting mixed numbers to improper fractions, accurately performing division, and ensuring that the final answer is simplified if necessary. Precision not only ensures the correct answer but also demonstrates a thorough understanding of the underlying mathematical principles.
Trends and Latest Developments
Increase in Online Math Resources
The advent of online education has led to a proliferation of math resources, from interactive tutorials to video explanations. Platforms like Khan Academy and Coursera offer comprehensive courses that cover arithmetic, algebra, and beyond. These resources often emphasize conceptual understanding and problem-solving skills, catering to diverse learning styles. Many of these platforms also provide adaptive learning tools that adjust to the student's pace and skill level, making math education more accessible and personalized.
Focus on Conceptual Understanding
Modern math education increasingly emphasizes conceptual understanding over rote memorization. Instead of simply memorizing formulas, students are encouraged to understand the underlying principles and logic behind mathematical operations. This approach fosters critical thinking and problem-solving skills, enabling students to apply mathematical concepts to real-world scenarios. This shift is reflected in educational standards and curricula worldwide, promoting a deeper, more meaningful engagement with mathematics.
Use of Technology in Math Education
Technology plays an increasingly important role in math education. Interactive software, graphing calculators, and online simulations provide students with opportunities to explore mathematical concepts in a dynamic and engaging way. These tools can help visualize abstract ideas, making them more accessible and intuitive. Furthermore, technology enables educators to track student progress and provide personalized feedback, enhancing the learning experience.
Gamification of Math
To make learning math more enjoyable, educators are increasingly using gamification techniques. Math games and apps incorporate game mechanics such as points, badges, and leaderboards to motivate students and foster a sense of achievement. These games can help students practice arithmetic skills, improve problem-solving abilities, and develop a positive attitude towards mathematics.
Data-Driven Instruction
Data-driven instruction involves using data on student performance to inform teaching practices. Educators analyze assessment data to identify areas where students are struggling and tailor their instruction accordingly. This approach allows for more targeted and effective teaching, ensuring that students receive the support they need to succeed. Data-driven instruction is becoming increasingly prevalent in schools, supported by advancements in educational technology and data analytics.
Tips and Expert Advice
Double-Check Your Work
It might seem obvious, but always double-check your work, especially when dealing with fractions and mixed numbers. Simple errors in arithmetic can lead to incorrect answers, so it's worth taking the extra time to verify each step of your calculation. Start by reviewing your initial setup to make sure you correctly interpreted the problem. Then, carefully check each step of your calculation, paying attention to details like carrying numbers and simplifying fractions. If possible, use a calculator to verify your answer, but be sure to understand the underlying principles so you can identify any errors.
Practice Regularly
Like any skill, proficiency in mathematics requires regular practice. The more you practice, the more comfortable you'll become with different types of problems and the more confident you'll be in your ability to solve them. Set aside some time each day or week to work on math problems, starting with the basics and gradually progressing to more challenging topics. Use online resources, textbooks, or workbooks to find practice problems, and don't be afraid to ask for help if you get stuck. Consistency is key to building a solid foundation in mathematics.
Break Down Complex Problems
When faced with a complex math problem, it can be helpful to break it down into smaller, more manageable steps. This allows you to focus on each step individually, reducing the likelihood of errors and making the problem seem less daunting. Start by identifying the key components of the problem and outlining the steps you need to take to solve it. Then, work through each step methodically, checking your work as you go. By breaking down the problem into smaller parts, you can make it easier to understand and solve.
Understand the "Why"
Instead of simply memorizing formulas and procedures, try to understand the underlying principles and logic behind mathematical concepts. This will not only make it easier to remember the formulas but also enable you to apply them to a wider range of problems. When you understand the "why" behind the math, you'll be better equipped to solve problems creatively and adapt to new situations. This deeper understanding will also make math more engaging and enjoyable.
Use Visual Aids
Visual aids can be a powerful tool for understanding mathematical concepts. Diagrams, charts, and graphs can help you visualize abstract ideas and see the relationships between different quantities. For example, when working with fractions, you can use pie charts or bar graphs to represent the fractions visually. Similarly, when working with geometric concepts, you can use diagrams to illustrate shapes and their properties. Experiment with different types of visual aids to find what works best for you, and don't hesitate to create your own.
FAQ
Q: What is a mixed number? A: A mixed number is a number consisting of a whole number and a fraction combined into one "mixed" number, such as 47 1/4.
Q: How do I convert a mixed number to an improper fraction? A: Multiply the whole number by the denominator of the fraction, add the numerator, and then place the result over the original denominator. For example, 47 1/4 becomes (47 * 4 + 1) / 4 = 189/4.
Q: Why do we convert mixed numbers to improper fractions? A: Converting to improper fractions makes it easier to perform multiplication and division operations.
Q: What does "half of" mean in mathematics? A: "Half of" means to divide by 2. It's equivalent to finding 50% or multiplying by 0.5.
Q: How do you divide a fraction by 2? A: You can divide the numerator by 2 if it's even, or multiply the denominator by 2. For example, half of 1/4 is 1/(4*2) = 1/8.
Conclusion
In summary, finding half of 47 and 1/4 requires converting the mixed number to an improper fraction and then dividing by 2. By converting 47 1/4 to 189/4, we then divide 189/4 by 2, which equals 189/8, or 23 and 5/8. Accuracy and understanding the basics of fractions are critical. Whether you're a student, a professional, or just someone looking to brush up on your math skills, mastering these calculations can be incredibly valuable. Now that you have a thorough understanding of how to tackle this type of problem, why not try a few practice questions? Share your answers or any questions you still have in the comments below – let's keep the learning going!
Latest Posts
Latest Posts
-
69 Inches To Feet And Inches
Nov 16, 2025
-
How To Convert Kcal To Joules
Nov 16, 2025
-
How Are Elements And Atoms Different
Nov 16, 2025
-
How To Solve A Equation Using Substitution
Nov 16, 2025
-
Experimental And Quasi Experimental Designs For Research
Nov 16, 2025
Related Post
Thank you for visiting our website which covers about What Is Half Of 47 And 1 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.