What Is 5 8 Equal To
catholicpriest
Nov 17, 2025 · 11 min read
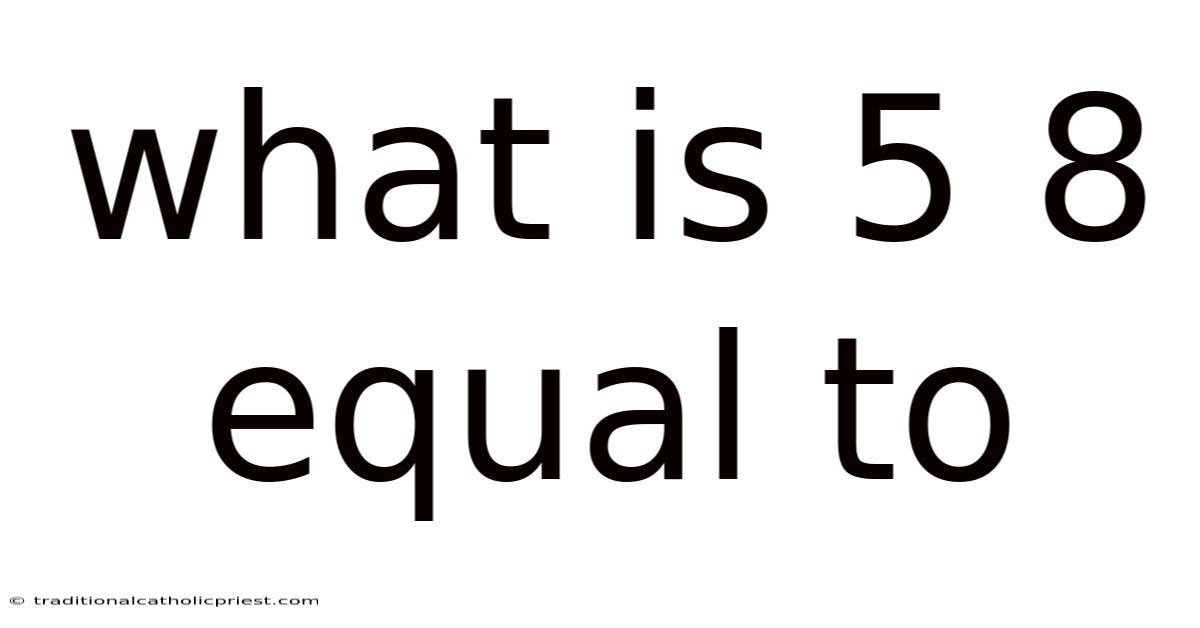
Table of Contents
The question "what is 5/8 equal to" may seem straightforward, but it opens the door to understanding fractions, decimals, percentages, and their real-world applications. Fractions are a fundamental part of mathematics, and understanding how to manipulate them is crucial for everyday calculations, from cooking to construction. Let's dive into the specifics of the fraction 5/8 and explore its various representations and practical uses.
Understanding the Fraction 5/8
The fraction 5/8 represents a part of a whole, where the whole is divided into 8 equal parts, and we are considering 5 of those parts. In mathematical terms, 5 is the numerator, which indicates the number of parts we have, and 8 is the denominator, which tells us the total number of equal parts the whole is divided into. Understanding this basic structure is key to grasping what 5/8 truly means and how it relates to other numerical forms.
Fractions are an integral part of everyday life, appearing in contexts ranging from cooking recipes to measuring ingredients. Knowing how to work with fractions, including converting them into other forms like decimals and percentages, is a valuable skill. This article will provide a comprehensive overview of the fraction 5/8, exploring its definition, historical context, different representations, practical applications, current trends, and expert advice to equip you with a solid understanding of this essential mathematical concept.
Comprehensive Overview of 5/8
To fully understand the fraction 5/8, we need to delve into its definitions, scientific foundations, historical context, and essential concepts. This comprehensive overview will provide a robust foundation for appreciating the significance of fractions in mathematics and beyond.
Definition and Basic Concepts
The fraction 5/8 is a rational number that represents a part of a whole. As mentioned earlier, the number 5 is the numerator, and 8 is the denominator. A fraction is considered proper if the numerator is less than the denominator, which is the case with 5/8. This means that 5/8 represents a value less than one whole unit. Fractions can also be improper, where the numerator is greater than or equal to the denominator (e.g., 9/8), representing a value greater than or equal to one.
Understanding the relationship between the numerator and denominator is essential. The denominator tells us how many equal parts the whole is divided into, while the numerator tells us how many of those parts we are considering. In the case of 5/8, we are looking at 5 out of 8 equal parts.
Scientific and Mathematical Foundations
The concept of fractions is deeply rooted in mathematics and has been used for thousands of years. Fractions are a fundamental part of number theory and are essential for understanding rational numbers. Rational numbers are numbers that can be expressed as a fraction p/q, where p and q are integers and q is not zero.
The mathematical operations involving fractions (addition, subtraction, multiplication, and division) follow specific rules that ensure accuracy and consistency. For example, when adding or subtracting fractions, a common denominator is required. This means finding the least common multiple (LCM) of the denominators and converting the fractions to equivalent forms with the common denominator.
Historical Context of Fractions
Fractions have a rich history dating back to ancient civilizations. The Egyptians, for example, used fractions extensively in their calculations, particularly in land surveying and construction. They primarily used unit fractions (fractions with a numerator of 1) and had a unique way of representing other fractions as sums of unit fractions.
The Babylonians also made significant contributions to the development of fractions. They used a base-60 number system, which allowed them to represent fractions with greater accuracy. Their system influenced the way we measure time (60 seconds in a minute, 60 minutes in an hour) and angles (360 degrees in a circle).
The modern notation for fractions, with the numerator above a horizontal line and the denominator below, became widely adopted during the Middle Ages. Mathematicians like Leonardo Fibonacci played a crucial role in popularizing this notation and promoting the use of fractions in various calculations.
Converting 5/8 to Decimal Form
To convert the fraction 5/8 to a decimal, you simply divide the numerator (5) by the denominator (8). The calculation is as follows:
5 ÷ 8 = 0.625
Therefore, 5/8 is equal to 0.625 in decimal form. This conversion is essential because decimals are often easier to work with in calculations, especially when using calculators or computers.
Converting 5/8 to Percentage Form
To convert the fraction 5/8 to a percentage, you first convert it to a decimal (as shown above) and then multiply by 100. The calculation is as follows:
- 625 × 100 = 62.5%
Thus, 5/8 is equal to 62.5%. Percentages are widely used in various contexts, such as calculating discounts, interest rates, and statistical data.
Trends and Latest Developments Involving Fractions
Fractions may seem like a basic mathematical concept, but they continue to play a vital role in modern applications. Current trends and developments in mathematics education and practical applications highlight the ongoing relevance of understanding fractions.
Modern Mathematics Education
In contemporary mathematics education, there is a renewed emphasis on conceptual understanding rather than rote memorization. Educators are using visual aids, hands-on activities, and real-world examples to help students grasp the underlying principles of fractions. This approach aims to make learning more engaging and effective, ensuring that students can apply their knowledge of fractions in various contexts.
Technology also plays a crucial role in modern mathematics education. Interactive simulations, educational apps, and online resources provide students with opportunities to explore fractions in a dynamic and interactive way. These tools can help students visualize fractions, manipulate them, and solve problems more effectively.
Applications in Computer Science
Fractions are essential in computer science, particularly in areas such as image processing, data compression, and algorithm design. For example, image scaling algorithms often involve fractional scaling factors to resize images proportionally. Similarly, data compression techniques may use fractional representations to reduce the size of data files.
In algorithm design, fractions are used to represent probabilities, ratios, and proportions. Many algorithms rely on fractional calculations to make decisions and optimize performance. Understanding fractions is therefore crucial for computer scientists and software engineers.
Financial Applications
Fractions are ubiquitous in financial calculations. Interest rates, stock prices, and investment returns are often expressed as fractions or percentages. For example, a stock price may increase by 1/4 of a point, or an investment may yield a return of 3 1/2%.
In personal finance, understanding fractions is essential for budgeting, managing debt, and making informed financial decisions. For example, calculating the proportion of income spent on housing, transportation, and other expenses involves working with fractions.
Cooking and Baking
Fractions are a fundamental part of cooking and baking. Recipes often specify ingredients in fractional amounts, such as 1/2 cup of flour, 1/4 teaspoon of salt, or 3/4 cup of sugar. Accurate measurement is crucial for achieving the desired results, and understanding fractions is essential for scaling recipes up or down.
In professional kitchens, chefs and bakers rely on their knowledge of fractions to create consistent and high-quality dishes. They often need to adjust recipes to accommodate different batch sizes or substitute ingredients while maintaining the correct proportions.
Construction and Engineering
Fractions are widely used in construction and engineering for measuring lengths, areas, volumes, and angles. Architects, engineers, and construction workers need to work with fractions to ensure that structures are built accurately and safely.
For example, measuring the dimensions of a room, calculating the slope of a roof, or determining the amount of material needed for a project involves working with fractions. Understanding fractions is therefore essential for professionals in these fields.
Tips and Expert Advice for Working with Fractions
Working with fractions can sometimes be challenging, but with the right strategies and techniques, it can become much easier. Here are some practical tips and expert advice to help you master fractions.
Simplify Fractions
Simplifying fractions involves reducing them to their simplest form by dividing both the numerator and denominator by their greatest common factor (GCF). For example, the fraction 4/8 can be simplified to 1/2 by dividing both 4 and 8 by their GCF, which is 4.
Simplifying fractions makes them easier to work with and understand. It also helps to avoid errors in calculations. Always check if a fraction can be simplified before performing any operations.
Use Visual Aids
Visual aids such as diagrams, charts, and models can be helpful for understanding fractions, especially for visual learners. For example, you can use a pie chart to represent a fraction, with each slice representing a part of the whole.
Visual aids can also be used to compare fractions and perform operations such as addition and subtraction. By visualizing the fractions, you can gain a better understanding of their relationships and how they interact with each other.
Practice Regularly
Like any mathematical skill, mastering fractions requires practice. The more you work with fractions, the more comfortable and confident you will become. Try to incorporate fractions into your daily life, such as when cooking, shopping, or managing your finances.
There are also many online resources and educational apps that offer practice problems and quizzes on fractions. Use these tools to reinforce your understanding and track your progress.
Convert to Decimals or Percentages When Appropriate
In some cases, it may be easier to work with fractions by converting them to decimals or percentages. This is especially true when using calculators or computers, which typically perform calculations using decimals.
However, it is important to understand the relationship between fractions, decimals, and percentages and to be able to convert between them fluently. This will give you the flexibility to choose the form that is most convenient for the task at hand.
Understand Common Denominators
When adding or subtracting fractions, you need to find a common denominator. This means finding a number that is a multiple of both denominators and converting the fractions to equivalent forms with the common denominator.
The least common multiple (LCM) is the smallest number that is a multiple of both denominators. Using the LCM as the common denominator simplifies the calculations and reduces the risk of errors.
Use Real-World Examples
Relating fractions to real-world examples can help you understand their practical applications and make them more meaningful. For example, you can use fractions to calculate the proportion of ingredients in a recipe, the discount on a sale item, or the amount of time spent on different activities.
By seeing how fractions are used in everyday life, you can develop a deeper appreciation for their importance and relevance.
Frequently Asked Questions (FAQ) About the Fraction 5/8
Here are some frequently asked questions about the fraction 5/8, along with concise and informative answers:
Q: What is 5/8 as a decimal? A: 5/8 is equal to 0.625 as a decimal.
Q: What is 5/8 as a percentage? A: 5/8 is equal to 62.5% as a percentage.
Q: Is 5/8 a proper or improper fraction? A: 5/8 is a proper fraction because the numerator (5) is less than the denominator (8).
Q: How do you simplify 5/8? A: 5/8 is already in its simplest form because 5 and 8 have no common factors other than 1.
Q: Can 5/8 be expressed as a mixed number? A: No, 5/8 cannot be expressed as a mixed number because it is a proper fraction (less than 1).
Q: How do you convert 5/8 to a fraction with a denominator of 16? A: Multiply both the numerator and denominator by 2: (5 * 2) / (8 * 2) = 10/16.
Q: What are some real-world examples of using 5/8? A: Examples include measuring ingredients in cooking (e.g., 5/8 cup of flour), calculating proportions in construction, and representing data in statistics.
Conclusion
In conclusion, the fraction 5/8 is a fundamental mathematical concept with wide-ranging applications in various fields. It is equal to 0.625 in decimal form and 62.5% in percentage form. Understanding what 5/8 represents and how to convert it into other forms is essential for everyday calculations and problem-solving. From cooking and baking to construction and finance, fractions play a crucial role in ensuring accuracy and precision.
We encourage you to continue exploring the world of fractions and their applications. Practice converting fractions to decimals and percentages, solve real-world problems involving fractions, and deepen your understanding of this essential mathematical concept. Share your insights and questions in the comments below, and let's continue the conversation about the fascinating world of fractions!
Latest Posts
Latest Posts
-
Akbar Or Birbal Story In Hindi
Nov 17, 2025
-
Why Do Humans Have Hair On Their Body
Nov 17, 2025
-
Is News An Acronym For Something
Nov 17, 2025
-
Angles In A Triangle Add Up To
Nov 17, 2025
-
What Are The 5 Spheres Of Earth
Nov 17, 2025
Related Post
Thank you for visiting our website which covers about What Is 5 8 Equal To . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.