What Is 125 As A Fraction
catholicpriest
Nov 13, 2025 · 10 min read
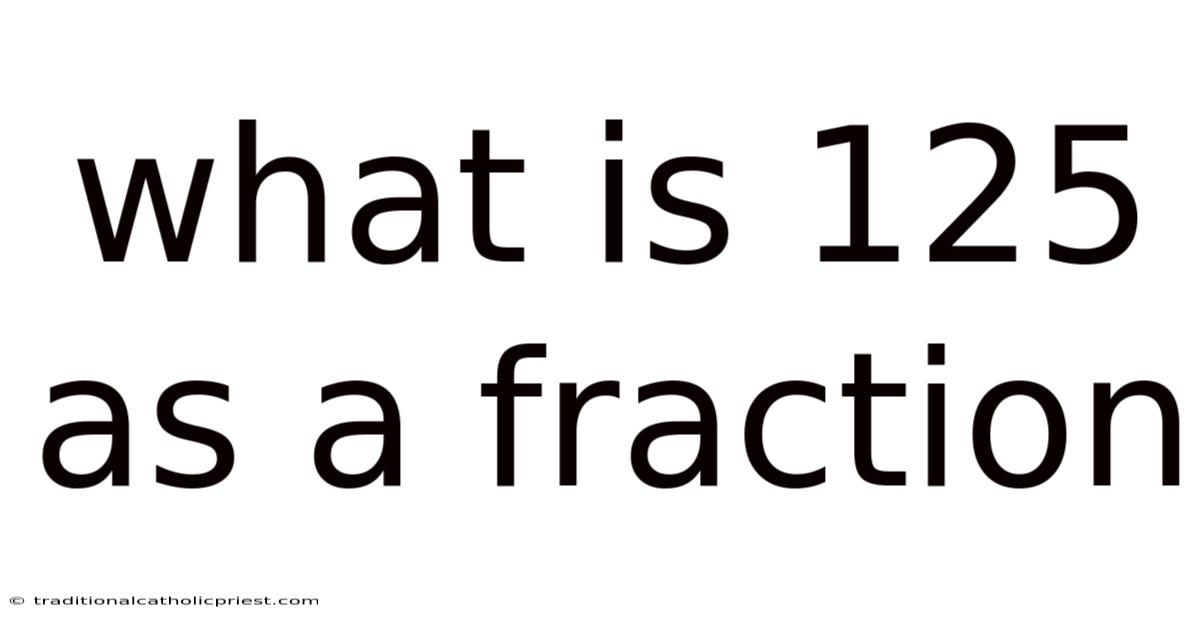
Table of Contents
Imagine you're at a bakery, and the baker offers you a deal: you can have 1.25 of a delicious pie. Sounds tempting, right? But what exactly does 1.25 of a pie mean? It's more than one whole pie, but less than two. This is where understanding how to express 1.25 as a fraction becomes incredibly useful. It lets us see the exact quantity we're talking about, broken down into understandable parts.
Converting decimals to fractions is a fundamental skill in mathematics with real-world applications far beyond bakery scenarios. Whether you're calculating ingredient ratios in a recipe, figuring out discounts while shopping, or even understanding financial reports, knowing how to express 1.25 as a fraction (or any decimal for that matter) will empower you with a clearer, more precise understanding of the numbers around you. So, let's dive into the process of transforming the decimal 1.25 into its fractional equivalent.
Understanding the Basics: Converting 1.25 to a Fraction
To convert 1.25 to a fraction, we must first recognize that 1.25 is a decimal number. Decimal numbers are based on powers of 10. The number 1.25 can be read as "one and twenty-five hundredths." This reading is key to understanding how to write it as a fraction. The digits after the decimal point represent fractions with denominators that are powers of 10, such as 10, 100, 1000, and so on.
The process involves a few straightforward steps:
- Write the decimal as a fraction: Express 1.25 as a fraction by placing it over 1. Since any number divided by 1 remains the same, this doesn't change the value: 1.25/1.
- Eliminate the decimal: Multiply both the numerator (top number) and the denominator (bottom number) by a power of 10 that will shift the decimal point to the right until the numerator becomes a whole number. In this case, multiplying by 100 will do the trick: (1.25 * 100) / (1 * 100) = 125/100.
- Simplify the fraction: Reduce the fraction to its simplest form by finding the greatest common divisor (GCD) of the numerator and denominator, and then dividing both by it. The GCD of 125 and 100 is 25. Dividing both by 25, we get: (125 ÷ 25) / (100 ÷ 25) = 5/4.
Therefore, 1.25 expressed as a fraction in its simplest form is 5/4. This fraction can also be expressed as a mixed number, which is 1 1/4 (one and one-quarter).
A Comprehensive Overview of Fractions, Decimals, and Conversions
To truly understand the conversion of 1.25 into a fraction, it’s helpful to explore the concepts of fractions, decimals, and the relationship between them. This knowledge will provide a solid foundation for tackling more complex conversions and mathematical problems.
-
What is a Fraction?
A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, and the numerator indicates how many of those parts we are considering. For example, in the fraction 1/2, the whole is divided into two equal parts, and we are considering one of those parts. There are different types of fractions, including proper fractions (where the numerator is less than the denominator), improper fractions (where the numerator is greater than or equal to the denominator), and mixed numbers (a combination of a whole number and a proper fraction).
-
What is a Decimal?
A decimal is another way of representing numbers that are not whole. Decimal numbers are based on the base-10 number system, where each digit's position represents a power of 10. The digits to the right of the decimal point represent fractional parts of a whole. For example, in the decimal 0.75, the 7 is in the tenths place (7/10) and the 5 is in the hundredths place (5/100). So, 0.75 is equivalent to 75/100.
-
The Relationship Between Fractions and Decimals
Fractions and decimals are two different ways of representing the same values. Any fraction can be expressed as a decimal by dividing the numerator by the denominator. Conversely, any decimal can be expressed as a fraction by recognizing the place value of the digits after the decimal point and writing the decimal as a fraction with a denominator that is a power of 10.
-
Converting Decimals to Fractions: A Deeper Dive
The key to converting decimals to fractions is understanding place value. The first digit after the decimal point represents tenths, the second represents hundredths, the third represents thousandths, and so on. For example, the decimal 0.625 can be broken down as 6/10 + 2/100 + 5/1000. To convert this to a single fraction, you can write it as 625/1000. This fraction can then be simplified by finding the greatest common divisor (GCD) of the numerator and denominator.
-
Simplifying Fractions
Simplifying fractions involves reducing them to their lowest terms. This means finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by that number. For example, the fraction 75/100 can be simplified by finding the GCD of 75 and 100, which is 25. Dividing both the numerator and denominator by 25, we get 3/4. This is the simplest form of the fraction. Simplifying fractions makes them easier to understand and work with.
Trends and Latest Developments in Fraction and Decimal Usage
While the fundamental principles of fractions and decimals remain constant, their applications and the ways we interact with them are continually evolving. Here are some current trends and developments:
-
Increased Emphasis in Education: Math education is increasingly focusing on building a strong conceptual understanding of fractions and decimals from an early age. Educators are moving away from rote memorization and emphasizing hands-on activities and visual aids to help students grasp the underlying principles. This approach aims to equip students with the skills to apply these concepts in real-world scenarios.
-
Digital Tools and Calculators: Technology has made working with fractions and decimals easier than ever. Online calculators and apps can quickly convert between fractions and decimals, simplify fractions, and perform complex calculations. These tools are valuable for students, professionals, and anyone who needs to work with numbers.
-
Data Representation and Analysis: In the age of big data, fractions and decimals are used extensively to represent and analyze data. Percentages, which are a form of decimal, are used to express proportions and ratios. Understanding how to convert between fractions, decimals, and percentages is crucial for interpreting data and making informed decisions.
-
Financial Literacy: Fractions and decimals play a vital role in financial literacy. From calculating interest rates to understanding stock prices, a solid understanding of these concepts is essential for managing personal finances and making sound investment decisions.
-
Real-World Applications in STEM Fields: Science, Technology, Engineering, and Mathematics (STEM) fields rely heavily on fractions and decimals. Engineers use them to design structures and machines, scientists use them to conduct experiments and analyze data, and mathematicians use them to develop new theories and models.
Tips and Expert Advice for Mastering Fraction and Decimal Conversions
Converting between fractions and decimals can be a breeze with the right techniques and a bit of practice. Here are some tips and expert advice to help you master these conversions:
-
Memorize Common Conversions: Memorizing common fraction-decimal equivalents can save you time and effort. For example, knowing that 1/2 = 0.5, 1/4 = 0.25, and 3/4 = 0.75 can make calculations much faster. Create a flashcard set with these common conversions and review them regularly.
-
Practice Regularly: Like any skill, converting fractions and decimals requires practice. Work through a variety of problems, starting with simple conversions and gradually increasing the difficulty. The more you practice, the more comfortable and confident you will become. Websites and textbooks offer numerous practice problems.
-
Use Visual Aids: Visual aids can be incredibly helpful for understanding fractions and decimals. Use diagrams, charts, and models to visualize the concepts. For example, you can use a pie chart to represent fractions or a number line to represent decimals. Seeing the concepts visually can make them easier to grasp.
-
Break Down Complex Problems: When faced with a complex conversion problem, break it down into smaller, more manageable steps. For example, if you need to convert a mixed number to a decimal, first convert the fraction part to a decimal and then add it to the whole number.
-
Understand Place Value: A thorough understanding of place value is essential for converting decimals to fractions. Remember that the first digit after the decimal point represents tenths, the second represents hundredths, the third represents thousandths, and so on. This knowledge will help you write the decimal as a fraction with the correct denominator.
-
Simplify, Simplify, Simplify: Always simplify fractions to their lowest terms. This makes them easier to understand and work with. Find the greatest common divisor (GCD) of the numerator and denominator and divide both by that number.
-
Check Your Work: Always double-check your work to ensure accuracy. Use a calculator to verify your conversions or ask a friend or teacher to review your work. Accuracy is crucial when working with fractions and decimals.
FAQ About Converting Decimals to Fractions
Q: Why is it important to know how to convert decimals to fractions? A: Converting decimals to fractions is important because it allows you to express values in different forms, which can be useful in various situations. Fractions can provide a more precise representation of a number than decimals, especially when dealing with repeating decimals or complex ratios. Additionally, understanding both forms enhances your overall mathematical literacy.
Q: Can all decimals be converted into fractions? A: Yes, all terminating and repeating decimals can be converted into fractions. Terminating decimals (decimals that end) can be easily converted by placing the decimal over a power of 10 and simplifying. Repeating decimals require a slightly more complex algebraic method but can still be expressed as fractions.
Q: What is a repeating decimal, and how do I convert it to a fraction? A: A repeating decimal is a decimal that has a repeating pattern of digits after the decimal point (e.g., 0.333...). To convert it to a fraction, you can use an algebraic method. Let x equal the repeating decimal, multiply x by a power of 10 that shifts the repeating part to the left of the decimal point, and then subtract the original equation from the new equation. This will eliminate the repeating part, allowing you to solve for x as a fraction.
Q: What is the difference between a proper fraction and an improper fraction? A: A proper fraction is a fraction where the numerator is less than the denominator (e.g., 1/2). An improper fraction is a fraction where the numerator is greater than or equal to the denominator (e.g., 5/4). Improper fractions can be converted into mixed numbers (a whole number and a proper fraction).
Q: How do I convert a mixed number to an improper fraction? A: To convert a mixed number to an improper fraction, multiply the whole number by the denominator of the fraction, add the numerator, and then place the result over the original denominator. For example, to convert 1 1/4 to an improper fraction, multiply 1 by 4, add 1, and place the result over 4, giving you 5/4.
Conclusion
Understanding how to express 1.25 as a fraction, and more broadly, mastering the conversion between decimals and fractions, is a fundamental skill that empowers you in countless real-world scenarios. From baking and shopping to finance and data analysis, the ability to fluently translate between these numerical forms provides a deeper, more precise understanding of the world around you. By following the steps outlined, practicing regularly, and utilizing available tools, you can confidently navigate the world of numbers.
Ready to put your newfound knowledge into practice? Take a moment to try converting a few decimals into fractions, and vice versa. Share your results in the comments below, or ask any questions you may still have. Let's continue to explore the fascinating world of mathematics together!
Latest Posts
Latest Posts
-
Whats The Chemical Formula For Photosynthesis
Nov 13, 2025
-
How Are Conduction Convection And Radiation Different
Nov 13, 2025
-
What Is The Primary Energy Source For Life On Earth
Nov 13, 2025
-
Integration By Parts For Definite Integral
Nov 13, 2025
-
Solve For X In The Following Right Triangle
Nov 13, 2025
Related Post
Thank you for visiting our website which covers about What Is 125 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.