What Is 1/2 Of 1 3/4
catholicpriest
Nov 18, 2025 · 11 min read
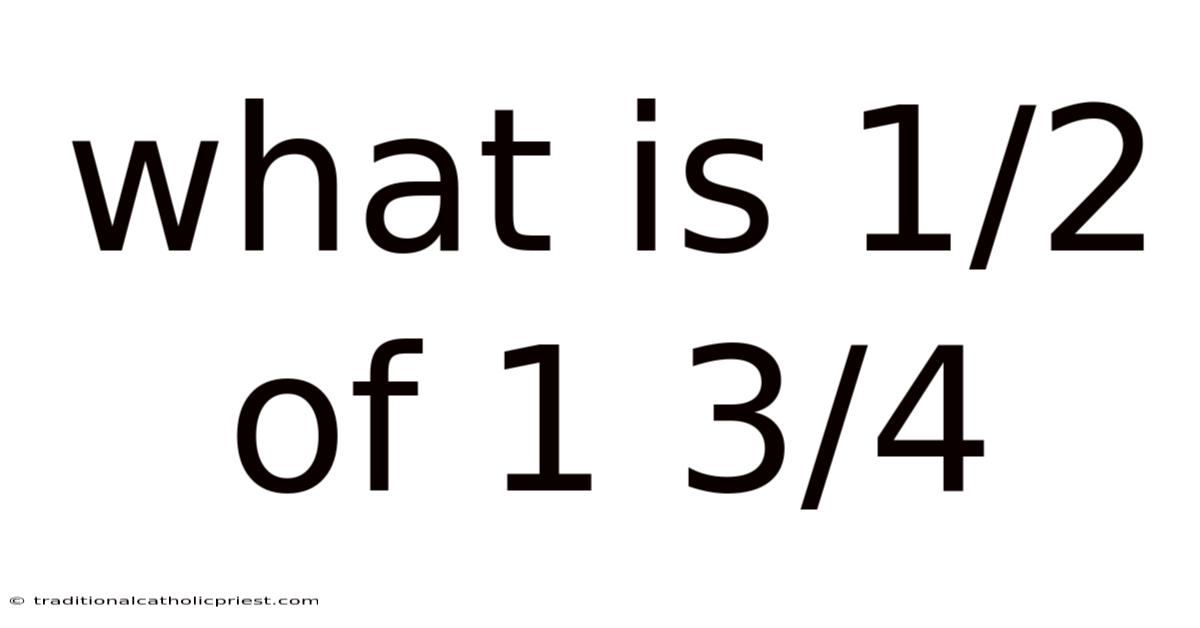
Table of Contents
Imagine you're baking a cake for a friend's birthday. The recipe calls for 1 ¾ cups of flour, but you realize you only want to make half the recipe. The question that pops into your head is, "What is half of 1 ¾ cups?" This simple baking scenario highlights a common need: understanding how to find a fraction of a mixed number. Whether it's adjusting recipes, splitting resources, or solving math problems, knowing how to calculate fractions of mixed numbers is a valuable skill.
Let's say you're planning a small garden and have 1 ¾ bags of soil. You decide to use only half of it for your initial planting. To determine exactly how much soil you'll use, you need to find half of 1 ¾. This practical example demonstrates the usefulness of this calculation in everyday situations. In this article, we will explore the concept of calculating a fraction of a mixed number, providing you with the knowledge and tools to tackle similar problems with confidence.
Main Subheading
Calculating a fraction of a mixed number might seem daunting at first, but it’s a straightforward process once you understand the underlying concepts. A mixed number combines a whole number and a fraction (e.g., 1 ¾), while a fraction represents a part of a whole (e.g., ½). Finding a fraction of a mixed number involves multiplying the fraction by the mixed number. This is commonly used in various fields, from cooking and baking to engineering and finance. Mastering this skill is not only beneficial for academic purposes but also highly practical in everyday life.
To begin, let’s break down the components. A mixed number like 1 ¾ can be thought of as 1 whole plus ¾ of another whole. A fraction like ½ represents one part out of two equal parts. The goal is to find what you get when you take ½ of the total amount represented by 1 ¾. There are a couple of ways to approach this: converting the mixed number to an improper fraction first or using the distributive property. The best method depends on personal preference and the specific problem at hand.
Comprehensive Overview
To understand the concept fully, let’s dive into definitions, scientific foundations, history, and essential concepts.
Definitions and Basic Concepts
- Fraction: A fraction represents a part of a whole, expressed as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). For example, in the fraction ½, 1 is the numerator and 2 is the denominator.
- Mixed Number: A mixed number is a combination of a whole number and a proper fraction (a fraction where the numerator is less than the denominator). For example, 1 ¾ is a mixed number with 1 as the whole number and ¾ as the fractional part.
- Improper Fraction: An improper fraction is a fraction where the numerator is greater than or equal to the denominator. For example, 5/4 is an improper fraction. Any mixed number can be converted into an improper fraction.
Scientific Foundations
The concept of fractions and mixed numbers is rooted in mathematics, specifically in the branch of arithmetic. The foundation lies in understanding how to represent parts of a whole and how these parts can be manipulated through mathematical operations like addition, subtraction, multiplication, and division. These operations are governed by mathematical rules and axioms that ensure consistency and accuracy in calculations.
History
Fractions have been used since ancient times. Egyptians used fractions as early as 1800 BC, primarily using unit fractions (fractions with a numerator of 1). The Babylonians used a base-60 number system, which facilitated the use of fractions. The concept of mixed numbers also has ancient roots, evolving as societies needed ways to quantify amounts that were more than whole units but not quite another whole unit. Over centuries, various cultures contributed to the development and refinement of fractional arithmetic, leading to the methods we use today.
Converting Mixed Numbers to Improper Fractions
One of the most useful techniques for working with mixed numbers is converting them into improper fractions. Here’s how to convert 1 ¾ to an improper fraction:
- Multiply the whole number by the denominator of the fraction: 1 * 4 = 4.
- Add the numerator to the result: 4 + 3 = 7.
- Place the result over the original denominator: 7/4.
So, 1 ¾ is equivalent to 7/4 as an improper fraction.
Multiplying Fractions
To multiply two fractions, you multiply the numerators together and the denominators together. For example, to find ½ of ¾:
(1/2) * (3/4) = (1 * 3) / (2 * 4) = 3/8
Calculating a Fraction of a Mixed Number: Step-by-Step
Let’s calculate ½ of 1 ¾ using the conversion method:
- Convert the mixed number 1 ¾ to an improper fraction: 1 ¾ = 7/4.
- Multiply the fraction ½ by the improper fraction 7/4: (1/2) * (7/4) = 7/8.
Therefore, ½ of 1 ¾ is 7/8.
Alternative Method: Distributive Property
Another approach is to use the distributive property. This involves breaking down the mixed number into its whole number and fractional parts and then distributing the multiplication.
- Separate the mixed number into its parts: 1 ¾ = 1 + ¾.
- Multiply the fraction by each part: (1/2) * 1 + (1/2) * (3/4).
- Calculate each product: (1/2) * 1 = 1/2 and (1/2) * (3/4) = 3/8.
- Add the results: 1/2 + 3/8. To add these, find a common denominator, which is 8.
- Convert 1/2 to 4/8 (multiply numerator and denominator by 4).
- Add the fractions: 4/8 + 3/8 = 7/8.
Using this method, we also find that ½ of 1 ¾ is 7/8.
Trends and Latest Developments
In recent years, educational approaches have increasingly emphasized the importance of understanding mathematical concepts through real-world applications. This trend has led to the development of interactive tools and resources that help students visualize and manipulate fractions and mixed numbers.
Educational Tools and Apps
Many educational apps and websites now offer interactive simulations and games that make learning about fractions more engaging. These tools often include features like virtual manipulatives, which allow students to physically represent fractions and mixed numbers and perform operations on them.
Data-Driven Insights
Educational research provides insights into how students learn and understand fractions. Studies have shown that students often struggle with the concept of fractions due to a lack of conceptual understanding. To address this, educators are encouraged to use visual aids, hands-on activities, and real-world examples to help students build a solid foundation in fractional arithmetic.
Common Core Standards
In the United States, the Common Core State Standards for Mathematics emphasize the importance of mastering fractions. The standards outline specific learning objectives for each grade level, ensuring that students develop a deep understanding of fractions and their applications. This has led to a greater focus on teaching fractions in a way that promotes conceptual understanding rather than rote memorization.
Expert Opinions
Mathematics educators and experts advocate for teaching fractions through problem-solving and real-world contexts. By presenting fractions in the context of everyday situations, educators can help students see the relevance of the topic and motivate them to learn. This approach also encourages students to develop critical thinking skills and apply their knowledge in meaningful ways.
Tips and Expert Advice
Here are some practical tips and expert advice for mastering the calculation of a fraction of a mixed number:
1. Practice Regularly
Consistent practice is key to mastering any mathematical concept. Work through a variety of problems involving different mixed numbers and fractions. Start with simpler problems and gradually increase the complexity. Use online resources, textbooks, or create your own problems to practice. The more you practice, the more confident and proficient you will become.
2. Visualize Fractions
Use visual aids such as fraction bars, pie charts, or drawings to visualize fractions and mixed numbers. Visualizing fractions can help you understand the relationships between different fractions and make it easier to perform operations on them. For example, when calculating ½ of 1 ¾, draw a diagram representing 1 ¾ and then shade in half of it to see the result visually.
3. Use Real-World Examples
Connect fractions to real-world situations to make the concept more relatable and meaningful. Use examples from cooking, baking, gardening, or any other activity that involves dividing quantities. For instance, if a recipe calls for 2 ½ cups of flour and you want to make half the recipe, calculate ½ of 2 ½. This helps you see the practical application of fractions and reinforces your understanding.
4. Master Conversion Techniques
Become proficient in converting mixed numbers to improper fractions and vice versa. This skill is essential for performing calculations involving mixed numbers. Practice converting various mixed numbers to improper fractions until you can do it quickly and accurately. Also, practice converting improper fractions back to mixed numbers to ensure a complete understanding.
5. Understand the Distributive Property
Learn how to apply the distributive property to calculate a fraction of a mixed number. This method can be particularly useful when dealing with larger mixed numbers. Break down the mixed number into its whole number and fractional parts, multiply each part by the fraction, and then add the results. This approach can simplify the calculation and make it easier to understand.
6. Check Your Work
Always check your work to ensure accuracy. After calculating a fraction of a mixed number, ask yourself if the answer makes sense. For example, if you are finding ½ of 1 ¾, the answer should be less than 1 ¾. If the answer seems unreasonable, review your calculations to identify any errors.
7. Seek Help When Needed
Don't hesitate to seek help from teachers, tutors, or online resources if you are struggling with fractions. Understanding fractions is a fundamental skill that builds upon itself, so it's important to address any difficulties early on. Ask questions, attend tutoring sessions, or use online tutorials to clarify any concepts you find confusing.
8. Use Technology
Take advantage of technology to help you with fraction calculations. There are many online calculators and apps that can quickly and accurately perform fraction operations. While it's important to understand the underlying concepts, using technology can save time and reduce the risk of errors, especially when dealing with complex calculations.
FAQ
Q: What is a mixed number?
A: A mixed number is a number consisting of a whole number and a proper fraction (where the numerator is less than the denominator). For example, 2 ½ is a mixed number.
Q: How do you convert a mixed number to an improper fraction?
A: To convert a mixed number to an improper fraction, multiply the whole number by the denominator of the fraction, add the numerator, and then place the result over the original denominator. For example, to convert 3 ¼ to an improper fraction: (3 * 4 + 1) / 4 = 13/4.
Q: What is an improper fraction?
A: An improper fraction is a fraction where the numerator is greater than or equal to the denominator. For example, 7/4 is an improper fraction.
Q: How do you multiply fractions?
A: To multiply fractions, multiply the numerators together and the denominators together. For example, (1/2) * (3/4) = (1 * 3) / (2 * 4) = 3/8.
Q: Can you use a calculator to find a fraction of a mixed number?
A: Yes, many calculators can perform fraction operations. You can enter the mixed number as an improper fraction or use a calculator that supports mixed number input.
Q: Why is it important to learn about fractions?
A: Fractions are essential for many real-world applications, including cooking, baking, construction, and finance. Understanding fractions can help you solve problems, make informed decisions, and succeed in various fields.
Q: Is there another way to find a fraction of a mixed number besides converting to an improper fraction?
A: Yes, you can use the distributive property. Break down the mixed number into its whole number and fractional parts, multiply each part by the fraction, and then add the results.
Q: How do you simplify fractions?
A: To simplify a fraction, divide both the numerator and the denominator by their greatest common divisor (GCD). For example, to simplify 4/8, divide both by 4, resulting in 1/2.
Conclusion
Calculating a fraction of a mixed number is a fundamental skill with wide-ranging applications. Whether you're adjusting a recipe or solving a complex mathematical problem, understanding how to perform these calculations is essential. By converting the mixed number to an improper fraction or by applying the distributive property, you can accurately determine the result. Remember to practice regularly, visualize fractions, and connect them to real-world examples to reinforce your understanding.
Now that you’ve learned how to calculate a fraction of a mixed number, put your knowledge to the test! Try solving a few practice problems, and don't hesitate to seek help if you encounter any difficulties. Share this article with friends or classmates who might find it helpful, and let us know in the comments if you have any questions or insights to share. Happy calculating!
Latest Posts
Latest Posts
-
3 By 3 Systems Of Equations
Nov 18, 2025
-
Does Gas Have A Definite Volume
Nov 18, 2025
-
182 Cm To Ft And Inches
Nov 18, 2025
-
What Is The Tool To Measure Angles
Nov 18, 2025
-
Number Of Protons Neutrons And Electrons In Oxygen
Nov 18, 2025
Related Post
Thank you for visiting our website which covers about What Is 1/2 Of 1 3/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.