There Are Infinitely Many Prime Numbers
catholicpriest
Nov 14, 2025 · 12 min read
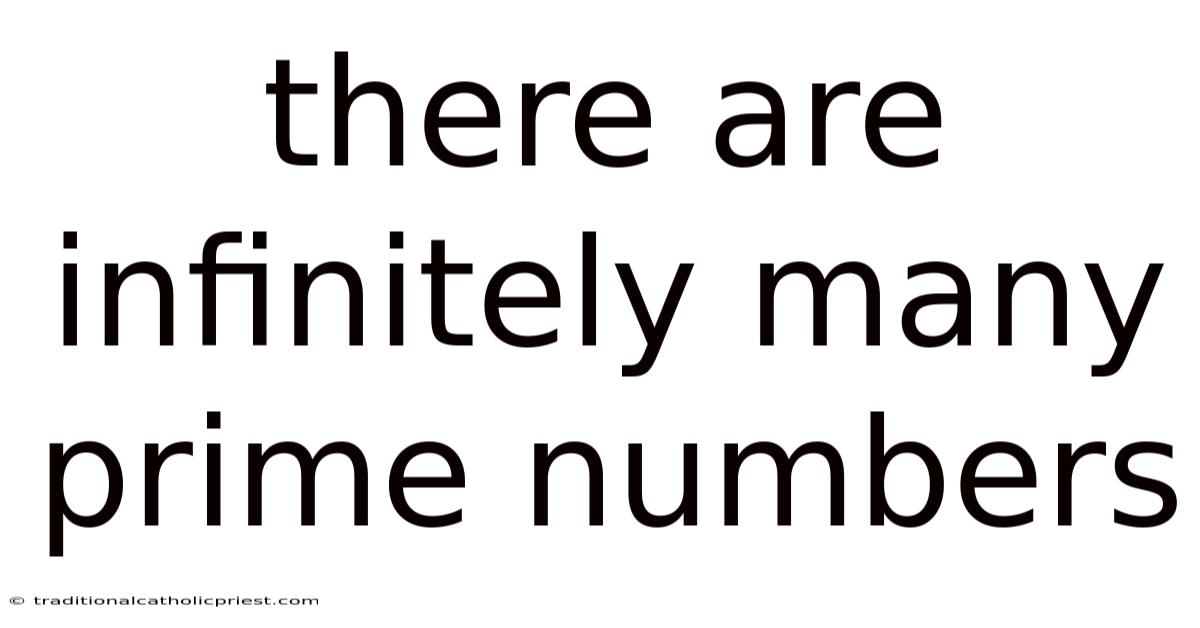
Table of Contents
Imagine you're a child, staring up at a night sky ablaze with stars. You start counting, but the vastness is overwhelming – it feels like they go on forever. That same sense of endlessness, of profound abundance, applies to a fundamental concept in mathematics: prime numbers. These fundamental building blocks of numbers, indivisible except by 1 and themselves, aren't just scattered sparsely; they are inexhaustibly plentiful.
Prime numbers hold a unique allure. They appear almost randomly amongst the integers, yet they underpin all other whole numbers through prime factorization. The question then arises: do these primes eventually thin out to nothing, or do they continue, an unending cascade of mathematical atoms? The answer, elegantly proven over two millennia ago, is that there are infinitely many prime numbers. This isn't just a mathematical curiosity; it's a cornerstone of number theory, with implications reaching far beyond abstract equations, influencing cryptography and computer science.
Main Subheading
The assertion that there are infinitely many prime numbers is one of the most fundamental and beautiful theorems in mathematics. But what does it really mean? At its core, it states that no matter how many prime numbers you discover, there will always be more. You can't simply list them all because the list never ends. The concept of infinity can be difficult to grasp, especially when applied to something as seemingly concrete as numbers. In the case of primes, it means that their distribution, though irregular, extends indefinitely along the number line.
The proof of this theorem is not just about arriving at the correct conclusion; it's about the journey of logical deduction. The most famous and arguably most elegant proof comes from Euclid, a Greek mathematician who lived over 2300 years ago. His proof, known for its simplicity and power, uses a method called reductio ad absurdum, or proof by contradiction. This involves assuming the opposite of what you want to prove and then showing that this assumption leads to a logical impossibility, thereby proving the original statement.
Comprehensive Overview
Euclid's proof begins by assuming that there are finitely many prime numbers. Let's say these primes are p1, p2, p3,..., pn. This means we've created a complete list of all prime numbers that exist. Euclid then cleverly constructs a new number, let's call it N, by multiplying all the primes in our list together and adding 1:
N = (p1 * p2 * p3 * ... * pn) + 1
Now, let's consider the properties of this number N. There are only two possibilities: either N is itself a prime number, or it is composite, meaning it can be divided by some prime number.
If N is prime, then we've immediately found a prime number that was not in our original list, contradicting our initial assumption that we had listed all prime numbers.
However, what if N is composite? In this case, it must be divisible by at least one prime number. Let's call this prime number p. Now, here's the crucial point: can p be one of the primes in our original list (p1, p2, p3,..., pn)?
Suppose p is one of the primes in our list. This means N and the product (p1 * p2 * p3 * ... * pn) are both divisible by p. If two numbers are divisible by p, their difference must also be divisible by p. The difference between N and (p1 * p2 * p3 * ... * pn) is simply 1:
N - (p1 * p2 * p3 * ... * pn) = 1
This implies that 1 is divisible by p. But this is impossible because the only number that divides 1 is 1 itself, and by definition, prime numbers are greater than 1. This contradiction shows that p cannot be one of the primes in our original list.
Therefore, regardless of whether N is prime or composite, we have found a prime number that was not in our original list. This contradicts our initial assumption that we had listed all prime numbers. Since our assumption leads to a contradiction, it must be false. Therefore, the opposite must be true: there are infinitely many prime numbers.
This proof is a testament to the power of logical reasoning. It doesn't tell us how to find these primes, but it guarantees their unending existence. It's a profound statement about the nature of numbers themselves.
Beyond Euclid's elegant proof, other proofs exist that offer different perspectives on the infinitude of primes. One such proof uses the properties of the Riemann zeta function, a central object of study in analytic number theory. While significantly more complex than Euclid's proof, it provides a different lens through which to view the distribution of primes. The Riemann zeta function is defined as an infinite sum:
ζ(s) = 1/1s + 1/2s + 1/3s + 1/4s + ...
where s is a complex number. A crucial property of the Riemann zeta function is its Euler product representation, which connects it directly to prime numbers:
ζ(s) = Π (1 - p-s)-1
where the product is taken over all prime numbers p. If there were only finitely many prime numbers, this product would be finite, and the Riemann zeta function would be well-behaved for all values of s greater than 1. However, it can be shown that the Riemann zeta function diverges as s approaches 1. This divergence implies that there must be infinitely many prime numbers to ensure the Euler product representation remains consistent. This proof, while more advanced, highlights the deep connections between prime numbers and other areas of mathematics.
Trends and Latest Developments
While the infinitude of prime numbers has been known for millennia, the study of their distribution and properties remains a vibrant area of research. Understanding how primes are scattered among the integers is a central problem in number theory. The Prime Number Theorem, for example, provides an asymptotic estimate for the number of primes less than a given number x. It states that the number of primes less than x is approximately x / ln(x), where ln(x) is the natural logarithm of x. This theorem gives us a sense of how the density of primes decreases as we move further along the number line.
The Riemann Hypothesis, one of the most famous unsolved problems in mathematics, is deeply connected to the distribution of prime numbers. It makes a precise conjecture about the location of the zeros of the Riemann zeta function. If proven, the Riemann Hypothesis would provide much tighter control over the distribution of primes, allowing mathematicians to predict their occurrence with greater accuracy. The quest to prove or disprove the Riemann Hypothesis continues to drive research in number theory.
Another area of active research involves finding large prime numbers. While the existence of infinitely many primes is assured, finding specific large primes is a computational challenge. Large prime numbers are crucial for cryptographic applications, such as RSA encryption, which relies on the difficulty of factoring large numbers into their prime factors. Organizations like the Great Internet Mersenne Prime Search (GIMPS) coordinate the efforts of volunteers around the world to search for Mersenne primes, which are primes of the form 2p - 1, where p is itself a prime number. The largest known prime numbers are typically Mersenne primes due to the efficiency of the Lucas-Lehmer primality test for numbers of this form.
Recently, there's been growing interest in prime gaps – the differences between consecutive prime numbers. While the average gap between primes increases as we go further along the number line (as suggested by the Prime Number Theorem), the distribution of these gaps is far from uniform. The Twin Prime Conjecture, another famous unsolved problem, posits that there are infinitely many pairs of prime numbers that differ by only 2 (e.g., 3 and 5, 5 and 7, 11 and 13). While a complete proof remains elusive, significant progress has been made in recent years, with mathematicians showing that there are infinitely many pairs of primes that differ by a bounded amount.
Furthermore, the search for prime numbers exhibiting specific patterns or properties is an ongoing endeavor. For example, mathematicians are interested in arithmetic progressions of primes, which are sequences of primes where the difference between consecutive terms is constant. The Green-Tao theorem proves that there exist arbitrarily long arithmetic progressions of prime numbers. This means that you can find sequences of primes with any desired length, where the difference between consecutive primes is the same throughout the sequence.
These trends and developments underscore the enduring fascination with prime numbers. From theoretical investigations into their distribution to practical applications in cryptography, the study of primes continues to be a central and dynamic area of mathematical research.
Tips and Expert Advice
Understanding the infinitude of prime numbers is one thing, but appreciating their significance and applying that understanding is another. Here are some tips and expert advice to deepen your comprehension and explore the fascinating world of primes:
-
Visualize the Distribution: Prime numbers can seem abstract, but visualizing their distribution can make them more concrete. Try plotting prime numbers on a number line or creating a graph that shows the number of primes less than a given value. This can help you see how the density of primes changes as you move along the number line and appreciate the irregularity of their distribution. You can use programming languages like Python with libraries such as Matplotlib to create these visualizations. Experiment with different scales and ranges to gain a better intuition for the spacing between primes.
-
Explore Prime Factorization: Prime factorization is the process of breaking down a composite number into its prime factors. Practice finding the prime factorization of different numbers. This exercise will solidify your understanding of what prime numbers are and how they serve as the building blocks of all other whole numbers. Start with small numbers and gradually work your way up to larger ones. You can use online tools or write your own code to automate the prime factorization process.
-
Study Different Proofs: Euclid's proof is the most famous, but explore other proofs of the infinitude of primes, such as the one using the Riemann zeta function or Euler's proof using harmonic series. Each proof offers a different perspective and highlights different connections to other areas of mathematics. Understanding these different approaches will give you a more comprehensive understanding of the concept.
-
Learn About Primality Tests: Explore different algorithms for determining whether a given number is prime. The simplest method is trial division, where you check if the number is divisible by any prime number less than its square root. More sophisticated tests, such as the Miller-Rabin test and the AKS primality test, are used for larger numbers. Understanding these tests will give you insight into the computational challenges of working with prime numbers.
-
Investigate Cryptographic Applications: Prime numbers are essential for modern cryptography. Learn about how prime numbers are used in encryption algorithms like RSA. Understanding the mathematical principles behind these algorithms will give you a practical appreciation for the importance of prime numbers in securing digital communication. You can explore online resources and tutorials to learn about the basics of cryptography and how prime numbers are used in practice.
-
Engage with Open Problems: The world of prime numbers is full of unsolved problems, such as the Riemann Hypothesis and the Twin Prime Conjecture. Learning about these problems can inspire you to think creatively and explore new ideas. Even if you don't solve them, you'll gain a deeper appreciation for the challenges and complexities of number theory.
By actively engaging with these tips and exploring the fascinating world of prime numbers, you can move beyond simply understanding the theorem and develop a deeper appreciation for their significance and beauty.
FAQ
Q: What exactly is a prime number?
A: A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. Examples include 2, 3, 5, 7, 11, and so on.
Q: Why are prime numbers important?
A: Prime numbers are fundamental building blocks of all other whole numbers and have crucial applications in cryptography, computer science, and other fields.
Q: What does it mean to say there are infinitely many prime numbers?
A: It means that there is no largest prime number. No matter how many primes you find, you can always find another one.
Q: How was it proven that there are infinitely many prime numbers?
A: The most famous proof is Euclid's proof by contradiction, which demonstrates that assuming a finite number of primes leads to a logical impossibility.
Q: Are prime numbers evenly distributed?
A: No, prime numbers are not evenly distributed. Their distribution becomes sparser as you move further along the number line.
Q: What is the Prime Number Theorem?
A: The Prime Number Theorem provides an estimate for the number of primes less than a given number. It states that the number of primes less than x is approximately x / ln(x).
Q: What is the Riemann Hypothesis and how does it relate to prime numbers?
A: The Riemann Hypothesis is an unsolved problem that makes a precise conjecture about the location of the zeros of the Riemann zeta function. If proven, it would provide much tighter control over the distribution of prime numbers.
Q: How are large prime numbers used in cryptography?
A: Large prime numbers are used in encryption algorithms like RSA, which relies on the difficulty of factoring large numbers into their prime factors to secure digital communication.
Conclusion
The theorem that there are infinitely many prime numbers is a cornerstone of number theory, a testament to the unending nature of mathematical discovery. Euclid's elegant proof, along with more modern approaches, guarantees that primes continue to exist, stretching out into the infinite expanse of numbers. From the practical applications in cryptography to the theoretical depths of the Riemann Hypothesis, prime numbers remain a source of fascination and a driving force behind mathematical innovation.
Now that you've explored the concept of infinite primes, why not delve deeper? Try your hand at finding prime factors of large numbers, research the Riemann Hypothesis, or explore the fascinating world of cryptography. Share your findings, ask questions, and join the ongoing conversation about these fundamental building blocks of mathematics. The universe of prime numbers is vast and waiting to be explored.
Latest Posts
Latest Posts
-
What Is The Antonym Of Encourage
Nov 14, 2025
-
What Is Another Name For A Zucchini
Nov 14, 2025
-
Where Is 1 2 On A Number Line
Nov 14, 2025
-
Types Of Cancer In The Blood
Nov 14, 2025
-
Choose The Correct Definition Of Electrical Charge
Nov 14, 2025
Related Post
Thank you for visiting our website which covers about There Are Infinitely Many Prime Numbers . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.