Square Root Of X Square Root Of X
catholicpriest
Nov 09, 2025 · 11 min read
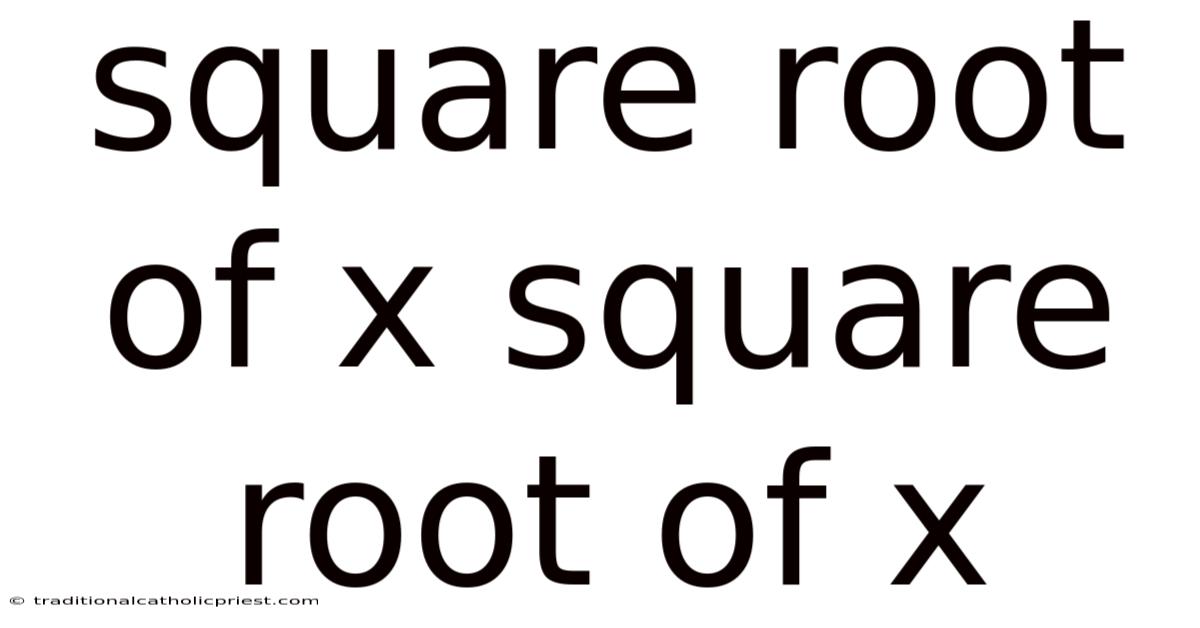
Table of Contents
Have you ever stared at a mathematical equation, feeling like you're lost in a maze of symbols and numbers? Perhaps you've encountered the square root of the square root of x and wondered, "What does this even mean, and how do I solve it?" Math, at times, can feel like learning a new language, where each symbol and equation has a story to tell.
The beauty of mathematics lies in its ability to simplify complex problems into manageable steps. Just as a painter uses strokes to create a masterpiece, mathematicians use operations to solve intricate equations. Consider the square root of the square root of x: a seemingly daunting problem that, with the right approach, becomes an elegant and straightforward solution. In this exploration, we'll demystify this concept, turning confusion into clarity and empowering you with the knowledge to tackle similar challenges.
Understanding the Square Root of the Square Root of x
At its core, the square root of the square root of x is a mathematical expression that involves taking the square root of x twice. This concept might seem complex at first glance, but breaking it down into simpler terms helps to clarify its meaning and applications. Understanding this expression requires familiarity with basic algebraic principles and the properties of square roots.
Mathematically, the expression can be written as √√x or (x<sup>1/2</sup>)<sup>1/2</sup>. These notations represent the same operation: first finding the square root of x, and then finding the square root of the result. This process is an example of nested mathematical operations, where one operation is performed within another. To fully grasp this concept, it's essential to understand what a square root is and how it behaves in different contexts. The square root of a number is a value that, when multiplied by itself, gives the original number. For instance, the square root of 9 is 3 because 3 * 3 = 9. This understanding is crucial for tackling more complex expressions like the square root of the square root of x.
Comprehensive Overview
To truly master the concept of the square root of the square root of x, it's important to delve into its definitions, mathematical foundations, historical context, and essential concepts. This exploration will provide a robust understanding and appreciation of this mathematical expression.
Definition and Mathematical Foundation
The square root of the square root of x can be defined as the fourth root of x. This is because taking the square root twice is equivalent to raising x to the power of 1/4. Mathematically, this is expressed as:
√√x = (x<sup>1/2</sup>)<sup>1/2</sup> = x<sup>(1/2)*(1/2)</sup> = x<sup>1/4</sup>
This definition is rooted in the properties of exponents and radicals. The exponent rule (a<sup>m</sup>)<sup>n</sup> = a<sup>mn</sup> is fundamental here, as it allows us to simplify the nested square roots into a single exponent. Understanding this rule is crucial for manipulating and simplifying expressions involving radicals and exponents.
The square root function, denoted as √x, is the inverse operation of squaring a number. That is, if y = √x, then y<sup>2</sup> = x. However, it's important to note that the square root function, when dealing with real numbers, typically returns the non-negative root. For example, while both 3 and -3 satisfy the equation y<sup>2</sup> = 9, the square root of 9 is generally taken to be 3.
Historical Context
The concept of square roots and nested radicals is ancient, dating back to the early days of mathematics. Ancient civilizations, such as the Babylonians and Egyptians, used square roots in various calculations, including land surveying, construction, and astronomy. While they may not have used the exact notation we use today, their understanding of square roots was sophisticated for their time.
The Greeks, particularly the Pythagoreans, further developed the theory of square roots and their relationship to geometry. They discovered irrational numbers, such as √2, which could not be expressed as a ratio of two integers. This discovery was a major breakthrough in mathematics and led to a deeper understanding of the number system.
In the Middle Ages, mathematicians in the Islamic world made significant contributions to algebra and the manipulation of radicals. They developed methods for solving equations involving square roots and other radicals, which were later transmitted to Europe. The notation and techniques we use today for working with square roots have evolved over centuries, building upon the work of these early mathematicians.
Essential Concepts
Several essential concepts are critical for understanding the square root of the square root of x:
- Radicals and Exponents: As mentioned earlier, understanding the relationship between radicals and exponents is fundamental. The nth root of x can be expressed as x<sup>1/n</sup>. This equivalence allows us to manipulate expressions more easily using the rules of exponents.
- Properties of Exponents: The rules of exponents, such as the power rule (a<sup>m</sup>)<sup>n</sup> = a<sup>mn</sup> and the product rule a<sup>m</sup> * a<sup>n</sup> = a<sup>m+n</sup>, are essential for simplifying expressions involving radicals.
- Domain and Range: The domain of the square root function is the set of all non-negative real numbers because the square root of a negative number is not a real number. The range of the square root function is also the set of all non-negative real numbers. When dealing with nested square roots, it's important to ensure that the argument of each square root is non-negative.
- Simplifying Radicals: Simplifying radicals involves expressing them in their simplest form. This often involves factoring the radicand (the number under the radical sign) and taking out any perfect square factors. For example, √8 can be simplified to 2√2.
- Rationalizing the Denominator: Rationalizing the denominator is a technique used to eliminate radicals from the denominator of a fraction. This is often done by multiplying the numerator and denominator by a suitable expression that will eliminate the radical in the denominator.
By mastering these concepts, you can confidently approach and solve problems involving the square root of the square root of x and other related expressions.
Trends and Latest Developments
In recent years, there has been a growing interest in the applications of radicals and exponents in various fields, including computer science, physics, and engineering. Here's a look at some of the trends and latest developments:
- Quantum Computing: In quantum computing, square roots and complex numbers play a crucial role. Quantum algorithms often involve manipulating complex amplitudes, which are represented using square roots. Understanding the properties of square roots is essential for designing and analyzing quantum algorithms.
- Data Analysis: In data analysis and machine learning, square roots are used in various statistical measures, such as standard deviation and root mean square error. These measures are used to quantify the spread or variability of data and to evaluate the performance of models.
- Cryptography: Square roots and modular arithmetic are used in cryptography to create secure communication protocols. For example, the Rabin cryptosystem relies on the difficulty of finding square roots modulo a composite number.
- Computer Graphics: In computer graphics and image processing, square roots are used in calculations involving distances, angles, and transformations. For example, the Euclidean distance between two points is calculated using the square root of the sum of the squares of the differences in their coordinates.
- Mathematical Software: Modern mathematical software, such as Mathematica, Maple, and MATLAB, provides powerful tools for working with radicals and exponents. These tools can be used to simplify expressions, solve equations, and visualize functions involving square roots.
Professional Insights
As a professional in the field of mathematics, I've observed that a strong foundation in basic algebraic principles, including the properties of radicals and exponents, is essential for success in many areas of science and engineering. Students who develop a deep understanding of these concepts are better equipped to tackle more advanced topics and to solve real-world problems.
One common mistake I've seen students make is neglecting to simplify expressions involving radicals. Simplifying radicals can often make subsequent calculations easier and can help to avoid errors. Another common mistake is forgetting to check the domain of the square root function when solving equations. It's important to ensure that the argument of each square root is non-negative to avoid extraneous solutions.
To stay up-to-date with the latest developments in mathematics, I recommend reading research papers in journals such as the American Mathematical Monthly, the Journal of Algebra, and the Journal of Number Theory. Additionally, attending conferences and workshops can provide opportunities to learn from experts in the field and to network with other mathematicians.
Tips and Expert Advice
Mastering the square root of the square root of x involves not just understanding the theory but also applying practical techniques. Here are some tips and expert advice to help you solve problems efficiently and accurately:
- Simplify Before You Solve: Always simplify the expression as much as possible before attempting to solve it. This can involve factoring the radicand, using the properties of exponents, or rationalizing the denominator. For example, consider the expression √(√(16x<sup>4</sup>)). First, simplify the inner square root: √(4x<sup>2</sup>), and then simplify the outer square root to get 2x. This step-by-step simplification makes the problem much easier to handle.
- Use Exponent Notation: Convert radicals to exponent notation to make use of the rules of exponents. For instance, √√x can be written as x<sup>1/4</sup>. This notation is particularly useful when dealing with complex expressions involving multiple radicals. The exponent notation makes it easier to apply the power rule and simplify the expression.
- Check for Extraneous Solutions: When solving equations involving square roots, always check your solutions to ensure that they are valid. Sometimes, squaring both sides of an equation can introduce extraneous solutions, which are solutions that satisfy the squared equation but not the original equation. For example, if you solve the equation √x = -2 by squaring both sides, you get x = 4. However, √4 = 2, not -2, so x = 4 is an extraneous solution.
- Practice Regularly: Like any mathematical skill, mastering the square root of the square root of x requires regular practice. Work through a variety of problems, starting with simple ones and gradually increasing in difficulty. This will help you build confidence and develop a deeper understanding of the concepts. Utilize online resources, textbooks, and practice worksheets to reinforce your skills.
- Understand the Domain: Always be mindful of the domain of the square root function. The argument of a square root must be non-negative. When solving equations or simplifying expressions, make sure that your solutions or simplifications do not violate this condition. For example, if you have the expression √(1 - x), then x must be less than or equal to 1 for the expression to be defined in the real number system.
By following these tips and advice, you can improve your problem-solving skills and gain a deeper understanding of the square root of the square root of x.
FAQ
Q: What is the square root of the square root of 16?
A: The square root of 16 is 4, and the square root of 4 is 2. Therefore, the square root of the square root of 16 is 2.
Q: How do I simplify √√81?
A: First, find the square root of 81, which is 9. Then, find the square root of 9, which is 3. So, √√81 = 3.
Q: Can I use a calculator to find the square root of the square root of a number?
A: Yes, most calculators have a square root function. You can input the number, press the square root button twice, and the calculator will give you the result. Alternatively, you can raise the number to the power of 0.25 (since √√x = x<sup>1/4</sup> = x<sup>0.25</sup>).
Q: What if I have √√(-16)?
A: The square root of a negative number is not a real number. Therefore, √√(-16) is not a real number. It involves complex numbers.
Q: Is there a general formula for finding the nth root of the mth root of x?
A: Yes, the nth root of the mth root of x can be written as x<sup>1/(nm)</sup>. For example, the cube root of the square root of x would be x<sup>1/(32)</sup> = x<sup>1/6</sup>.
Conclusion
In summary, the square root of the square root of x is a fundamental concept in algebra that can be expressed as x<sup>1/4</sup>. Understanding its definition, mathematical foundation, and historical context is crucial for mastering this concept. By simplifying expressions, using exponent notation, checking for extraneous solutions, practicing regularly, and being mindful of the domain, you can confidently solve problems involving nested square roots.
We encourage you to practice more problems and explore related concepts to deepen your understanding. Share your questions, insights, and problem-solving strategies in the comments below, and let's continue this mathematical journey together.
Latest Posts
Latest Posts
-
List All The Factors For 16
Nov 09, 2025
-
1 Meter Is How Much Cm
Nov 09, 2025
-
5 Letter Words Middle Letter O
Nov 09, 2025
-
90 Cm Equals How Many Inches
Nov 09, 2025
-
What Is The Difference Between Solutions Colloids And Suspensions
Nov 09, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of X Square Root Of X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.