Sin 2 X Cos 2 X
catholicpriest
Nov 10, 2025 · 12 min read
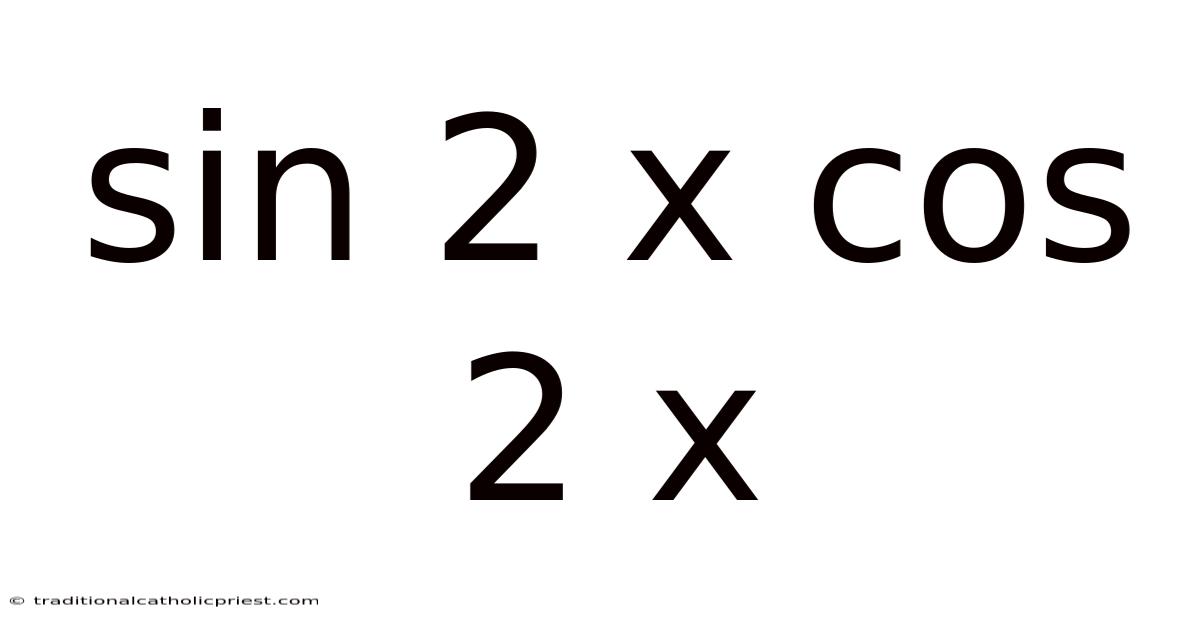
Table of Contents
The world of trigonometry can sometimes feel like navigating a complex maze, filled with seemingly abstract formulas and identities. However, beneath the surface lies an elegant framework that describes the relationships between angles and sides in triangles, unlocking powerful tools for solving problems in physics, engineering, and even art. Among these trigonometric expressions, sin 2x cos 2x stands out as a particularly interesting combination, one that reveals deeper connections within the trigonometric landscape and offers a gateway to understanding more advanced concepts.
Imagine you're designing a bridge, calculating the trajectory of a projectile, or even creating stunning visual effects for a film. Trigonometry provides the mathematical foundation for these endeavors, allowing you to model and predict real-world phenomena with remarkable accuracy. In this article, we will embark on a journey to unravel the mysteries of sin 2x cos 2x, exploring its definition, its relationship to other trigonometric identities, and its applications in various fields. We will also delve into practical tips and expert advice to help you master this concept and use it effectively in your own projects.
Main Subheading
The expression sin 2x cos 2x is a trigonometric product involving the sine and cosine of double angles. Before diving into the specifics of this expression, it's important to understand the fundamental concepts of trigonometric functions and double-angle formulas. Trigonometry, at its core, deals with the relationships between the angles and sides of triangles. The primary trigonometric functions are sine (sin), cosine (cos), and tangent (tan), which are defined based on the ratios of the sides of a right-angled triangle.
The sine of an angle is the ratio of the length of the opposite side to the hypotenuse, the cosine is the ratio of the adjacent side to the hypotenuse, and the tangent is the ratio of the opposite side to the adjacent side. These functions are not limited to right-angled triangles; they can be extended to any angle using the unit circle, which is a circle with a radius of 1 centered at the origin of a coordinate plane. In the unit circle, the sine and cosine of an angle correspond to the y and x coordinates of the point where the terminal side of the angle intersects the circle, respectively. Understanding these basic definitions is crucial for grasping the more complex concepts that follow.
Comprehensive Overview
Let’s begin with a more profound look into the definitions of sin 2x cos 2x and their scientific underpinnings.
Definitions and Scientific Foundations
The expression sin 2x cos 2x combines two fundamental trigonometric functions, sine and cosine, applied to double angles. The double angle formulas are derived from the angle sum formulas, which state that:
- sin(a + b) = sin a cos b + cos a sin b
- cos(a + b) = cos a cos b - sin a sin b
Setting a = b = x in these formulas yields the double angle formulas:
- sin 2x = 2 sin x cos x
- cos 2x = cos²x - sin²x
These formulas are the building blocks for understanding and manipulating trigonometric expressions involving double angles.
Derivation and Simplification
To further simplify the expression sin 2x cos 2x, we can use the double angle formulas directly. Recall that:
- sin 2x = 2 sin x cos x
- cos 2x = cos²x - sin²x
Substituting these into the expression, we get:
sin 2x cos 2x = (2 sin x cos x)(cos²x - sin²x)
This expression can be expanded as:
2 sin x cos³x - 2 sin³x cos x
While this expanded form is correct, it's often more useful to manipulate the original expression to achieve a more concise form. One common technique is to use the identity sin 2x = 2 sin x cos x. If we multiply and divide the original expression by 2, we get:
sin 2x cos 2x = (1/2) * (2 sin 2x cos 2x)
Now, notice that 2 sin 2x cos 2x has the same form as sin 2x, but with 2x instead of x. Thus, we can write:
2 sin 2x cos 2x = sin(2 * 2x) = sin 4x
Therefore,
sin 2x cos 2x = (1/2) sin 4x
This final form, (1/2) sin 4x, is a much simpler and more elegant representation of the original expression.
Relationship to Other Trigonometric Identities
The expression sin 2x cos 2x is closely related to several other trigonometric identities, making it a versatile tool in mathematical manipulations. For example, it can be linked to the Pythagorean identity:
sin²x + cos²x = 1
This identity is fundamental in trigonometry and can be used to express sin²x in terms of cos²x, or vice versa. Another important relationship is with the tangent function:
tan x = sin x / cos x
Using these identities, we can rewrite trigonometric expressions in various forms, making them easier to work with in different contexts. For instance, we can express sin 2x cos 2x in terms of tan x, although the resulting expression would be more complex and less useful in most cases.
Historical Context and Applications
Trigonometry has a rich history, dating back to ancient civilizations such as the Babylonians, Egyptians, and Greeks. These cultures used trigonometric concepts for surveying, navigation, and astronomy. The double angle formulas, including those used to simplify sin 2x cos 2x, were developed over centuries by mathematicians seeking to understand and predict celestial movements.
Today, trigonometry is used in a wide range of fields, including:
- Engineering: Calculating stresses and strains in structures, designing electrical circuits, and analyzing mechanical systems.
- Physics: Modeling wave phenomena, analyzing projectile motion, and studying optics and acoustics.
- Computer Graphics: Creating realistic 3D models, animating characters, and rendering scenes.
- Navigation: Determining position and course using GPS and other navigational tools.
The expression sin 2x cos 2x may not appear directly in all of these applications, but the underlying trigonometric principles are essential for solving complex problems in these fields.
Visual Representation
A visual representation can often enhance understanding of trigonometric functions. Consider the graph of y = sin 2x cos 2x. Since we know that sin 2x cos 2x = (1/2) sin 4x, we can easily graph this function. The graph is a sine wave with an amplitude of 1/2 and a period of π/2. The period is shorter than that of sin x because the argument of the sine function is 4x instead of x.
Visualizing the graph helps to understand the behavior of the function over different intervals. For example, we can see that the function oscillates between -1/2 and 1/2, and it completes one full cycle in a shorter interval than the standard sine function.
Trends and Latest Developments
In recent years, there has been a growing interest in using trigonometric functions and identities in advanced areas such as signal processing, image analysis, and machine learning. One trend is the use of trigonometric functions as activation functions in neural networks. Traditional activation functions like sigmoid and ReLU can sometimes lead to problems such as vanishing gradients. Trigonometric functions, with their periodic nature, can offer alternative activation functions that may improve the performance of neural networks in certain applications.
Another trend is the use of trigonometric functions in signal processing. The Fourier transform, which decomposes a signal into its constituent frequencies, relies heavily on sine and cosine functions. By manipulating trigonometric expressions, engineers can design filters and algorithms to analyze and process signals more efficiently.
From a professional perspective, staying up-to-date with these trends is crucial for anyone working in these fields. Understanding how trigonometric functions are being used in new and innovative ways can open up opportunities for research and development.
Tips and Expert Advice
Mastering sin 2x cos 2x and related trigonometric concepts requires a combination of theoretical knowledge and practical application. Here are some tips and expert advice to help you improve your understanding and skills:
-
Practice Regularly: The more you practice solving trigonometric problems, the more comfortable you will become with the concepts. Start with simple problems and gradually increase the difficulty level.
-
Understand the Unit Circle: The unit circle is a powerful tool for visualizing trigonometric functions and their relationships. Make sure you have a solid understanding of how the unit circle works and how to use it to find the values of sine, cosine, and tangent for different angles.
-
Memorize Key Identities: There are several key trigonometric identities that you should memorize, including the Pythagorean identity, the angle sum and difference formulas, and the double angle formulas. These identities will be invaluable for simplifying expressions and solving problems.
-
Use Online Resources: There are many excellent online resources available for learning trigonometry, including tutorials, videos, and practice problems. Take advantage of these resources to supplement your learning. Khan Academy, for example, offers a comprehensive trigonometry course that covers all the essential topics.
-
Seek Help When Needed: Don't be afraid to ask for help if you are struggling with a particular concept. Talk to your teacher, professor, or a tutor. There are also many online forums and communities where you can ask questions and get help from other students and experts.
-
Apply Trigonometry to Real-World Problems: One of the best ways to deepen your understanding of trigonometry is to apply it to real-world problems. Look for opportunities to use trigonometry in your everyday life, such as when calculating distances, angles, or heights.
-
Master the Double Angle Formulas: The double angle formulas are essential for simplifying expressions involving sin 2x cos 2x. Make sure you understand how to derive these formulas and how to use them in different contexts. Practice using the formulas to solve problems and simplify expressions.
-
Visualize Trigonometric Functions: Use graphing tools to visualize trigonometric functions and their transformations. This can help you understand how the functions behave and how they are related to each other. For example, you can graph y = sin 2x, y = cos 2x, and y = sin 2x cos 2x to see how they differ and how they are related.
-
Use Trigonometric Identities to Simplify Expressions: Trigonometric identities can be used to simplify complex expressions and make them easier to work with. Practice using identities to rewrite expressions in different forms and to solve equations.
-
Explore Advanced Topics: Once you have a solid understanding of the basics, explore more advanced topics such as trigonometric series, Fourier analysis, and complex numbers. These topics will deepen your understanding of trigonometry and its applications.
FAQ
Q: What is the value of sin 2x cos 2x when x = π/4?
A: To find the value of sin 2x cos 2x when x = π/4, we first substitute x = π/4 into the expression: sin(2 * π/4) cos(2 * π/4) = sin(π/2) cos(π/2) Since sin(π/2) = 1 and cos(π/2) = 0, the expression becomes: 1 * 0 = 0
Q: How can I simplify the expression sin 2x cos 2x?
A: To simplify the expression sin 2x cos 2x, you can use the double angle formula sin 2x = 2 sin x cos x. Rewrite the expression as: sin 2x cos 2x = (1/2) * (2 sin 2x cos 2x) Recognize that 2 sin 2x cos 2x is in the form of sin 2θ, where θ = 2x. Therefore: 2 sin 2x cos 2x = sin(2 * 2x) = sin 4x So, sin 2x cos 2x = (1/2) sin 4x
Q: What are the common mistakes to avoid when working with trigonometric identities?
A: Common mistakes when working with trigonometric identities include:
- Incorrectly applying identities: Make sure you are using the correct identity for the given situation.
- Forgetting the order of operations: Remember to follow the correct order of operations when simplifying expressions.
- Not checking for extraneous solutions: When solving trigonometric equations, always check your solutions to make sure they are valid.
- Assuming identities work for all values: Some identities may only be valid for certain values of x.
Q: How is sin 2x cos 2x used in real-world applications?
A: While the expression sin 2x cos 2x itself may not be directly used in many real-world applications, the underlying trigonometric principles and identities are essential in fields such as:
- Engineering: Calculating stresses and strains in structures, designing electrical circuits.
- Physics: Modeling wave phenomena, analyzing projectile motion.
- Computer Graphics: Creating realistic 3D models and animations.
- Navigation: Determining position and course using GPS.
Q: Can sin 2x cos 2x be expressed in terms of tan x?
A: Yes, sin 2x cos 2x can be expressed in terms of tan x, but the resulting expression is more complex. First, express sin 2x and cos 2x in terms of sin x and cos x: sin 2x = 2 sin x cos x cos 2x = cos²x - sin²x So, sin 2x cos 2x = 2 sin x cos x (cos²x - sin²x) Now, divide both sin x and cos x by cos x (assuming cos x ≠ 0) to introduce tan x = sin x / cos x: sin 2x cos 2x = 2 (sin x / cos x) cos²x (cos²x - sin²x) = 2 tan x cos^4 x (1 - tan²x) To express cos^4 x in terms of tan x, use the identity sec²x = 1 + tan²x and the fact that cos x = 1 / sec x: cos²x = 1 / sec²x = 1 / (1 + tan²x) cos^4 x = 1 / (1 + tan²x)² So, sin 2x cos 2x = 2 tan x [1 / (1 + tan²x)²] [1 - tan²x] = [2 tan x (1 - tan²x)] / (1 + tan²x)² This expression is more complex and less useful than the simplified form (1/2) sin 4x.
Conclusion
In summary, the expression sin 2x cos 2x is a fascinating example of how trigonometric functions and identities can be combined and simplified to reveal deeper mathematical relationships. By understanding the double angle formulas and other key trigonometric principles, we can manipulate this expression into a more concise and manageable form, such as (1/2) sin 4x. This simplification not only enhances our understanding of the expression itself but also provides a powerful tool for solving problems in various fields, from engineering and physics to computer graphics and navigation.
To further solidify your understanding of sin 2x cos 2x and related concepts, we encourage you to practice regularly, explore online resources, and apply your knowledge to real-world problems. Don't hesitate to seek help when needed and to delve into more advanced topics as your understanding grows. By mastering these fundamental principles, you will unlock a world of possibilities and gain a deeper appreciation for the beauty and power of trigonometry. Now, take the next step: try solving practice problems or exploring advanced topics related to trigonometric functions. Share your findings and questions in the comments below!
Latest Posts
Latest Posts
-
What Are The Least Common Multiples Of 9 And 12
Nov 10, 2025
-
Total Resistance In Parallel Circuit Calculator
Nov 10, 2025
-
What Are The Functions Of Vascular Tissue
Nov 10, 2025
-
How To Find Tan In Unit Circle
Nov 10, 2025
-
Is Table Salt A Compound Or Element
Nov 10, 2025
Related Post
Thank you for visiting our website which covers about Sin 2 X Cos 2 X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.