Simplify 1 X 1 X 2
catholicpriest
Nov 14, 2025 · 11 min read
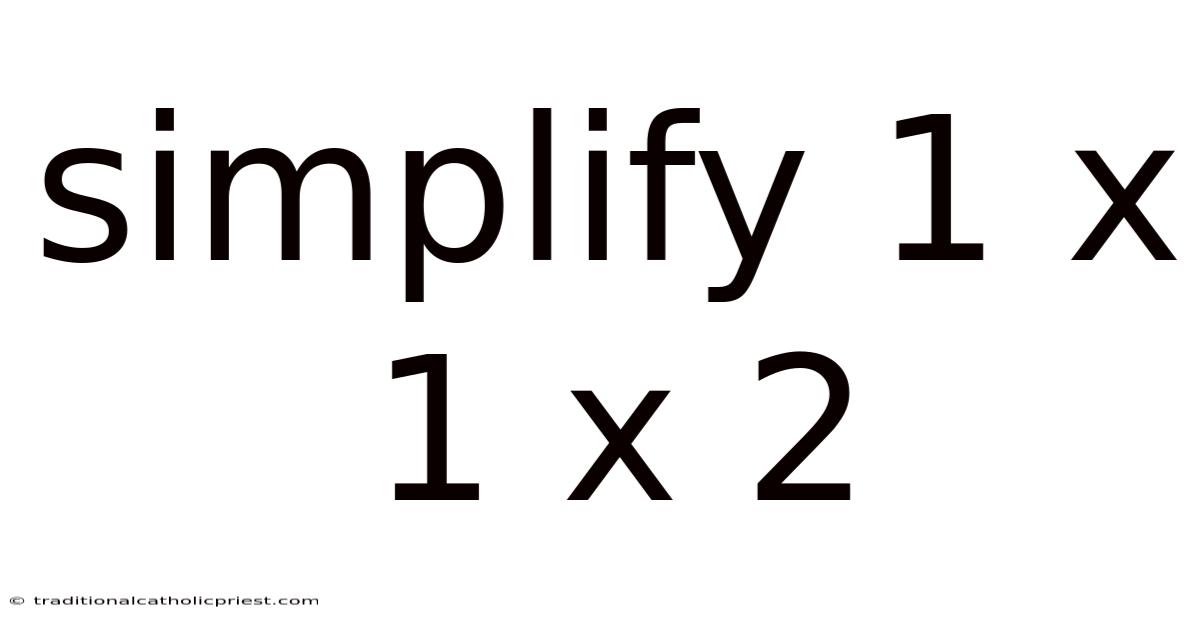
Table of Contents
Imagine you're organizing a child's playroom, surrounded by building blocks of various sizes. Among them, you spot a few peculiar ones: miniature rectangular prisms measuring exactly 1 x 1 x 2 units. These simple blocks, seemingly insignificant on their own, hold a fascinating property – they perfectly represent the fundamental idea of simplifying mathematical expressions. Just like these blocks can be arranged and combined in numerous ways, the expression "simplify 1 x 1 x 2" embodies the core principle of reducing complexity to its most basic form.
In the realm of mathematics, the act of simplification is akin to streamlining a complex process. It's about taking a convoluted equation or expression and reducing it to its most straightforward and understandable form without altering its fundamental value. The expression "simplify 1 x 1 x 2" may appear trivial at first glance, but it perfectly demonstrates this principle. It's an exercise in basic arithmetic, a gateway to understanding more complex algebraic manipulations. This article will delve into the intricacies of simplifying this seemingly simple expression, explore its broader mathematical context, and highlight the practical applications of such simplifications in various fields. From the basic rules of multiplication to the nuances of mathematical operations, we'll uncover the hidden depth within this elementary problem and reveal why mastering such fundamental concepts is crucial for building a strong foundation in mathematics.
Main Subheading
The process of simplifying mathematical expressions is a fundamental skill that underpins nearly every aspect of mathematics, from basic arithmetic to advanced calculus. At its core, simplification involves reducing an expression to its most concise and easily understandable form without changing its value. This often involves combining like terms, applying the order of operations, and using algebraic identities to rewrite expressions in a more manageable way. The goal is to make the expression easier to work with, whether for solving equations, evaluating functions, or understanding underlying mathematical relationships.
The expression "simplify 1 x 1 x 2" serves as an excellent starting point for understanding this concept. While seemingly elementary, it illustrates the basic principles of multiplication and the idea of reducing a series of operations to a single, simplified result. In essence, we are taking a sequence of multiplications and condensing it into a single numerical value. This seemingly simple process lays the groundwork for more complex simplifications involving variables, exponents, and more intricate mathematical functions. The ability to confidently and accurately simplify such expressions is crucial for success in higher-level mathematics and in many practical applications across various disciplines.
Comprehensive Overview
To fully appreciate the act of simplifying "1 x 1 x 2", it's essential to understand the underlying mathematical concepts that govern this operation. At its heart, this expression involves the fundamental operation of multiplication. Multiplication, in its simplest form, is repeated addition. For example, 3 x 4 is equivalent to adding 3 to itself four times (3 + 3 + 3 + 3 = 12). In the expression "1 x 1 x 2", we are performing a series of multiplications, each of which can be thought of as repeated addition in a specific context.
The order of operations, often remembered by the acronym PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction), dictates the sequence in which mathematical operations should be performed. While this expression doesn't involve parentheses or exponents, it does highlight the importance of understanding that multiplication is performed before addition or subtraction. In this case, we simply perform the multiplications from left to right, but in more complex expressions, adhering to the order of operations is critical for arriving at the correct answer.
In the expression "1 x 1 x 2," we first multiply 1 by 1, which results in 1. Then, we multiply this result (1) by 2, which gives us 2. Therefore, the simplified form of "1 x 1 x 2" is simply 2. This may seem trivial, but it demonstrates the core idea of taking a series of operations and reducing them to a single, simplified value. This principle extends to more complex algebraic expressions, where simplifying can involve combining like terms, factoring, and applying various algebraic identities.
The historical development of mathematical notation and operations provides further context for understanding simplification. Early mathematical systems often lacked the concise notation we use today, making calculations cumbersome and difficult to follow. The development of symbols like the multiplication sign "x" and the rules for order of operations were crucial steps in making mathematical expressions more manageable and understandable. These advancements allowed mathematicians to express complex ideas in a more compact and efficient way, facilitating the development of more advanced mathematical theories and applications.
Moreover, the concept of simplification is closely related to the idea of mathematical elegance and efficiency. Mathematicians often strive to find the simplest and most elegant solution to a problem, not just for aesthetic reasons but also because simpler solutions are often easier to understand, verify, and apply in other contexts. Simplifying an expression to its most basic form can reveal underlying patterns and relationships that might not be immediately apparent in the more complex original expression. Therefore, simplification is not just a technical skill but also a way of gaining deeper insight into the mathematical structures being studied.
Trends and Latest Developments
While the simplification of basic arithmetic expressions like "1 x 1 x 2" may seem far removed from the cutting edge of mathematical research, the underlying principles of simplification are still actively being explored and developed in various areas of mathematics and computer science. For example, in symbolic computation, researchers are developing algorithms and software tools that can automatically simplify complex algebraic expressions, manipulate equations, and perform symbolic integration and differentiation. These tools are used in a wide range of applications, from physics and engineering to finance and economics.
Another area where simplification plays a crucial role is in the development of efficient algorithms for solving optimization problems. Many real-world problems, such as scheduling, resource allocation, and logistics, can be formulated as optimization problems that involve finding the best solution from a large set of possibilities. Simplifying the problem formulation, identifying relevant constraints, and using appropriate mathematical techniques can significantly reduce the computational complexity of solving these problems.
In the field of machine learning, simplification techniques are used to build more interpretable and generalizable models. Complex machine learning models, such as deep neural networks, can often achieve high accuracy on training data but may be difficult to understand and prone to overfitting. Techniques like regularization, pruning, and knowledge distillation aim to simplify these models by reducing the number of parameters, removing redundant connections, and extracting essential features. The goal is to create models that are not only accurate but also easier to interpret and more robust to variations in the input data.
Furthermore, the rise of quantum computing has spurred research into new simplification techniques for quantum circuits and algorithms. Quantum circuits, which are used to implement quantum computations, can be extremely complex and difficult to optimize. Researchers are developing methods for simplifying these circuits by reducing the number of quantum gates, rearranging the order of operations, and exploiting quantum symmetries. These simplifications are essential for building practical quantum computers that can solve problems beyond the capabilities of classical computers.
Finally, data science leverages simplification techniques to extract meaningful insights from large and complex datasets. For example, dimensionality reduction techniques, such as principal component analysis (PCA) and t-distributed stochastic neighbor embedding (t-SNE), are used to reduce the number of variables in a dataset while preserving the essential information. This simplification makes it easier to visualize the data, identify patterns, and build predictive models. In essence, simplification remains a core principle driving innovation across diverse scientific and technological domains.
Tips and Expert Advice
Simplifying mathematical expressions effectively requires a combination of understanding fundamental principles and developing practical skills. One of the most important tips is to master the order of operations (PEMDAS/BODMAS). This ensures that you perform calculations in the correct sequence, leading to accurate results. Start by addressing any parentheses or brackets, then exponents, followed by multiplication and division (from left to right), and finally addition and subtraction (from left to right). Consistent application of this order will prevent common errors and make even complex expressions more manageable.
Another crucial tip is to break down complex expressions into smaller, more manageable steps. Don't try to do everything at once. Instead, identify the individual operations and simplify them one at a time. For example, if you have an expression with multiple terms and operations, focus on simplifying each term separately before combining them. This step-by-step approach reduces the cognitive load and minimizes the chance of making mistakes. It also allows you to check your work more easily and identify any errors along the way.
Practice regularly with a variety of problems to build your skills and confidence. Start with simple expressions and gradually work your way up to more complex ones. The more you practice, the more comfortable you will become with the different types of operations and the various techniques for simplifying them. Look for patterns and shortcuts that can help you simplify expressions more efficiently. For instance, recognizing common algebraic identities, such as the difference of squares or the square of a binomial, can save you time and effort.
Utilize available resources and tools to support your learning. There are many online calculators and software packages that can help you check your work and explore different simplification techniques. However, be sure to use these tools as a supplement to your own understanding, not as a replacement for it. Focus on understanding the underlying principles and developing your own skills, rather than relying solely on technology. Also, don't hesitate to seek help from teachers, tutors, or classmates if you are struggling with a particular concept or problem.
Finally, develop a habit of checking your work carefully after each step of the simplification process. Look for common errors, such as sign errors, arithmetic mistakes, or incorrect application of the order of operations. If possible, try to simplify the expression in a different way to verify your answer. This can help you catch errors that you might have missed the first time around. By developing a systematic approach to checking your work, you can significantly improve your accuracy and reduce the likelihood of making mistakes.
FAQ
Q: What does it mean to simplify a mathematical expression?
A: Simplifying a mathematical expression means reducing it to its most basic and easily understandable form without changing its value. This often involves combining like terms, applying the order of operations, and using algebraic identities to rewrite the expression in a more manageable way.
Q: Why is simplifying mathematical expressions important?
A: Simplifying expressions makes them easier to work with, whether for solving equations, evaluating functions, or understanding underlying mathematical relationships. It also helps in identifying patterns and relationships that might not be immediately apparent in the more complex original expression.
Q: What is the order of operations, and why is it important?
A: The order of operations (PEMDAS/BODMAS) dictates the sequence in which mathematical operations should be performed: Parentheses/Brackets, Exponents/Orders, Multiplication and Division (from left to right), Addition and Subtraction (from left to right). Following this order is crucial for arriving at the correct answer.
Q: Can a mathematical expression be simplified in more than one way?
A: Yes, sometimes there can be multiple ways to simplify an expression, but all valid methods should lead to the same simplified result.
Q: What are some common mistakes to avoid when simplifying expressions?
A: Common mistakes include ignoring the order of operations, making sign errors, incorrectly combining like terms, and misapplying algebraic identities. Checking your work carefully after each step can help avoid these errors.
Conclusion
In conclusion, the seemingly trivial exercise of "simplify 1 x 1 x 2" unveils the fundamental importance of simplification in mathematics. This process, at its core, is about reducing complexity to its most manageable form while preserving the inherent value of the expression. Mastering this simple skill lays the groundwork for tackling more complex algebraic manipulations and problem-solving scenarios. From basic arithmetic to advanced algorithms, the ability to simplify expressions efficiently is a cornerstone of mathematical proficiency and its application across diverse fields.
Now that you've explored the intricacies of simplifying basic mathematical expressions, take the next step. Practice with different examples, explore online resources, and challenge yourself with progressively complex problems. Embrace the process of simplification as a tool for understanding and problem-solving, and you'll be well on your way to mastering the art of mathematical clarity. Start simplifying today and unlock the potential for deeper mathematical understanding!
Latest Posts
Latest Posts
-
How To Write Book Review Example
Nov 14, 2025
-
Five Letter Word Starting With O U
Nov 14, 2025
-
What Does A Female Egg Look Like
Nov 14, 2025
-
Subtraction Of Fractions With Different Denominators
Nov 14, 2025
-
Scale Factor Of 2 3 Dilation
Nov 14, 2025
Related Post
Thank you for visiting our website which covers about Simplify 1 X 1 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.