Lim 1/x As X Approaches Infinity
catholicpriest
Nov 16, 2025 · 10 min read
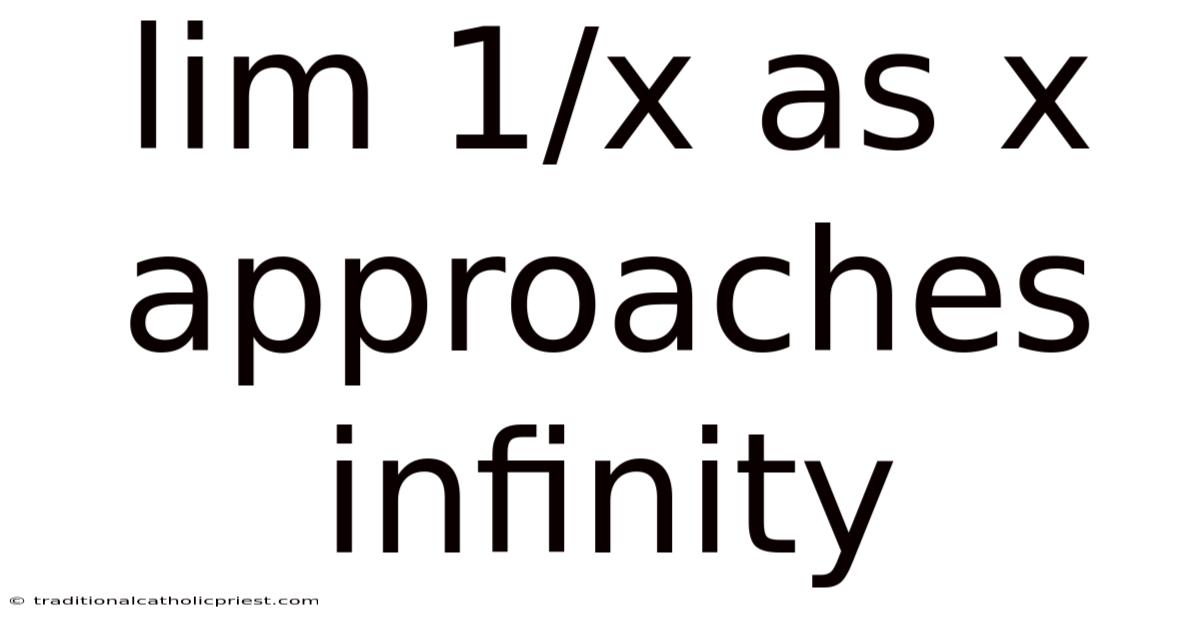
Table of Contents
Imagine you are walking on a path that stretches endlessly forward. With each step, the ground beneath you seems to flatten, the incline diminishing until it's almost imperceptible. This feeling of approaching a level plane is akin to understanding the concept of lim 1/x as x approaches infinity. It's a fundamental idea in calculus that describes what happens to the value of the fraction 1/x as 'x' grows larger and larger, moving towards infinity.
In mathematics, infinity is not a number but rather a concept representing something without any bound. When we explore lim 1/x as x approaches infinity, we're essentially asking: "What value does the fraction 1/x get closer and closer to as 'x' becomes unimaginably large?" The answer, perhaps intuitively, is zero. However, the beauty of calculus lies in its ability to rigorously define and prove such seemingly simple concepts, providing a foundation for understanding more complex phenomena. This article aims to delve into the depths of this limit, exploring its significance, applications, and nuances.
The Essence of Limits: A Mathematical Compass
To fully grasp lim 1/x as x approaches infinity, it's crucial to understand the concept of limits itself. In calculus, a limit describes the value that a function "approaches" as the input (or independent variable) approaches some value. This value can be a specific number, positive infinity, or negative infinity. Limits are the bedrock upon which calculus is built, forming the foundation for understanding derivatives, integrals, and continuity.
Limits allow us to analyze the behavior of functions at points where the function may not be explicitly defined or where standard algebraic manipulation is insufficient. For example, consider the function f(x) = (x^2 - 1) / (x - 1). At x = 1, this function is undefined because it leads to division by zero. However, we can explore the limit of this function as x approaches 1. By factoring the numerator, we get f(x) = (x + 1)(x - 1) / (x - 1). For all x ≠ 1, we can cancel the (x - 1) terms, simplifying the function to f(x) = x + 1. Therefore, the limit as x approaches 1 is lim (x→1) f(x) = lim (x→1) (x + 1) = 2. This exemplifies how limits allow us to examine a function's behavior near a point, even if the function is not defined at that point.
Limits are not just abstract mathematical tools; they have profound applications in physics, engineering, economics, and computer science. They are used to model rates of change, optimize processes, and analyze the stability of systems. Understanding limits provides a crucial lens for interpreting the world around us through a mathematical framework.
A Comprehensive Overview of Lim 1/x as x Approaches Infinity
Let's dive deeper into the heart of lim 1/x as x approaches infinity. The notation for this limit is written as:
lim (x→∞) 1/x
This notation tells us that we want to find the value that 1/x approaches as x becomes infinitely large. To understand this intuitively, imagine substituting increasingly larger values for 'x' in the fraction 1/x:
- If x = 1, then 1/x = 1
- If x = 10, then 1/x = 0.1
- If x = 100, then 1/x = 0.01
- If x = 1000, then 1/x = 0.001
- If x = 1,000,000, then 1/x = 0.000001
As you can see, as 'x' grows larger, the value of 1/x gets smaller and smaller, approaching zero. This intuitive understanding can be formalized with a more rigorous definition using the epsilon-delta definition of a limit.
The epsilon-delta definition states that for any arbitrarily small positive number ε (epsilon), there exists a number M such that if x > M, then |1/x - 0| < ε. In simpler terms, no matter how close to zero you want 1/x to be (defined by ε), you can always find a value M such that if x is larger than M, then 1/x will be within that close proximity to zero.
To prove lim 1/x as x approaches infinity using the epsilon-delta definition, we need to show that for any ε > 0, there exists an M such that if x > M, then |1/x - 0| < ε. Let's choose M = 1/ε. Then, if x > M, we have x > 1/ε. Taking the reciprocal of both sides (and noting that both x and ε are positive), we get 1/x < ε. Therefore, |1/x - 0| = |1/x| = 1/x < ε, which satisfies the epsilon-delta definition.
This rigorous proof confirms our intuitive understanding that as 'x' approaches infinity, 1/x approaches zero. The elegance of this limit lies in its simplicity and its fundamental role in calculus and analysis.
The concept of lim 1/x as x approaches infinity has its roots in the development of calculus by Isaac Newton and Gottfried Wilhelm Leibniz in the late 17th century. While they didn't have the same rigorous definition of limits that we use today, their work laid the foundation for understanding infinitesimal quantities and their relationship to infinitely large quantities. Augustin-Louis Cauchy, in the 19th century, formalized the epsilon-delta definition of a limit, providing a more precise and rigorous framework for calculus. This formalization was crucial for resolving controversies surrounding the use of infinitesimals and for establishing calculus on a solid mathematical foundation.
Trends and Latest Developments in Limit Analysis
The analysis of limits, including lim 1/x as x approaches infinity, continues to be an active area of research in mathematics. While the basic principles are well-established, mathematicians are exploring more complex and nuanced aspects of limits, including:
-
Non-standard Analysis: This field provides a rigorous framework for working with infinitesimals and infinitely large numbers, offering an alternative approach to calculus that complements the standard epsilon-delta approach.
-
Asymptotic Analysis: This branch of mathematics focuses on the behavior of functions as their input approaches a certain value, often infinity. It's widely used in physics, engineering, and computer science to approximate solutions to complex problems.
-
Limits in Higher Dimensions: The concept of limits extends to functions of multiple variables. Analyzing limits in higher dimensions can be significantly more challenging than in one dimension, as there are infinitely many paths along which a variable can approach a given point.
-
Computational Methods for Evaluating Limits: With the increasing power of computers, researchers are developing algorithms and software tools to evaluate limits numerically and symbolically. These tools are invaluable for solving complex problems in science and engineering.
One interesting trend is the use of machine learning to approximate limits of functions. By training machine learning models on a dataset of known limits, researchers are developing algorithms that can predict the limits of new functions with high accuracy. This approach has the potential to revolutionize the field of limit analysis, making it possible to solve problems that were previously intractable.
Tips and Expert Advice for Mastering Limits
Mastering the concept of limits, including lim 1/x as x approaches infinity, requires a combination of theoretical understanding and practical application. Here are some tips and expert advice to help you develop a solid foundation:
-
Grasp the Intuitive Meaning: Before diving into the formal definitions, make sure you understand the intuitive meaning of a limit. Visualizing the behavior of functions as their input approaches a certain value can be incredibly helpful. For lim 1/x as x approaches infinity, imagine the graph of y = 1/x. As you move further to the right along the x-axis (towards infinity), the graph gets closer and closer to the x-axis (y = 0).
-
Master the Epsilon-Delta Definition: The epsilon-delta definition is the foundation of rigorous limit analysis. While it can be challenging to grasp at first, understanding this definition is crucial for proving limits and understanding more advanced concepts in calculus. Work through examples carefully and practice applying the definition to different functions.
-
Practice, Practice, Practice: The best way to master limits is to practice solving problems. Start with simple examples and gradually work your way up to more complex ones. Pay attention to the different techniques that can be used to evaluate limits, such as factoring, rationalizing, and using L'Hôpital's rule.
-
Understand Limit Laws: Limit laws provide a set of rules for manipulating limits. These laws can be used to simplify complex expressions and evaluate limits more easily. For example, the limit of a sum is the sum of the limits, and the limit of a product is the product of the limits (provided that the individual limits exist).
-
Visualize Limits Graphically: Graphing functions and visualizing their behavior near a certain point can provide valuable insights into the concept of limits. Use graphing calculators or software to explore the behavior of different functions and to verify your solutions.
-
Seek Help When Needed: Don't be afraid to ask for help if you're struggling with limits. Talk to your teacher, classmates, or a tutor. There are also many online resources available, such as tutorials, videos, and forums.
-
Connect Limits to Real-World Applications: Understanding how limits are used in real-world applications can make the concept more engaging and relevant. Explore examples of limits in physics, engineering, economics, and computer science.
FAQ: Your Burning Questions Answered
Here are some frequently asked questions about lim 1/x as x approaches infinity:
Q: Why is infinity not a number? A: Infinity represents a concept of something without any bound or limit. It's not a specific value that you can perform arithmetic operations on in the same way you would with real numbers.
Q: Can a function approach infinity? A: Yes, a function can approach infinity as its input approaches a certain value. For example, the function f(x) = 1/x approaches infinity as x approaches 0 from the positive side.
Q: Is lim (x→∞) 1/x exactly equal to zero? A: Yes, in the standard real number system, the limit of 1/x as x approaches infinity is exactly equal to zero. This means that 1/x gets arbitrarily close to zero as x becomes infinitely large.
Q: What is L'Hôpital's rule and when can I use it? A: L'Hôpital's rule is a technique for evaluating limits of indeterminate forms, such as 0/0 or ∞/∞. It states that if the limit of f(x)/g(x) as x approaches a certain value is an indeterminate form, then the limit is equal to the limit of f'(x)/g'(x), where f'(x) and g'(x) are the derivatives of f(x) and g(x), respectively.
Q: How are limits used in calculus? A: Limits are fundamental to calculus. They are used to define derivatives, integrals, and continuity. The derivative of a function is defined as the limit of the difference quotient, and the integral of a function is defined as the limit of a Riemann sum.
Conclusion
Understanding lim 1/x as x approaches infinity is a cornerstone of calculus and a gateway to understanding more advanced mathematical concepts. This seemingly simple limit encapsulates the essence of limits: the ability to analyze the behavior of functions as their input approaches a particular value. By grasping the intuitive meaning, mastering the formal definitions, and practicing problem-solving, you can develop a solid foundation in limit analysis and unlock its power to solve problems in a wide range of fields.
Now that you have a comprehensive understanding of lim 1/x as x approaches infinity, we encourage you to delve deeper into the fascinating world of calculus. Explore other types of limits, learn about derivatives and integrals, and discover the many applications of calculus in science, engineering, and beyond. Share this article with your friends and colleagues who are also interested in learning more about calculus, and let's continue to explore the beauty and power of mathematics together. What other mathematical concepts pique your interest? Let us know in the comments below!
Latest Posts
Latest Posts
-
How Many Nuclei In Cardiac Muscle
Nov 16, 2025
-
Does Voltage Stay The Same In A Parallel Circuit
Nov 16, 2025
-
How Do You Know A Chemical Change Has Occurred
Nov 16, 2025
-
Cuanto Es Una Hectarea En Acres
Nov 16, 2025
-
What Unit Is Weight Measured In
Nov 16, 2025
Related Post
Thank you for visiting our website which covers about Lim 1/x As X Approaches Infinity . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.