Least Common Multiple Of 3 6
catholicpriest
Nov 17, 2025 · 10 min read
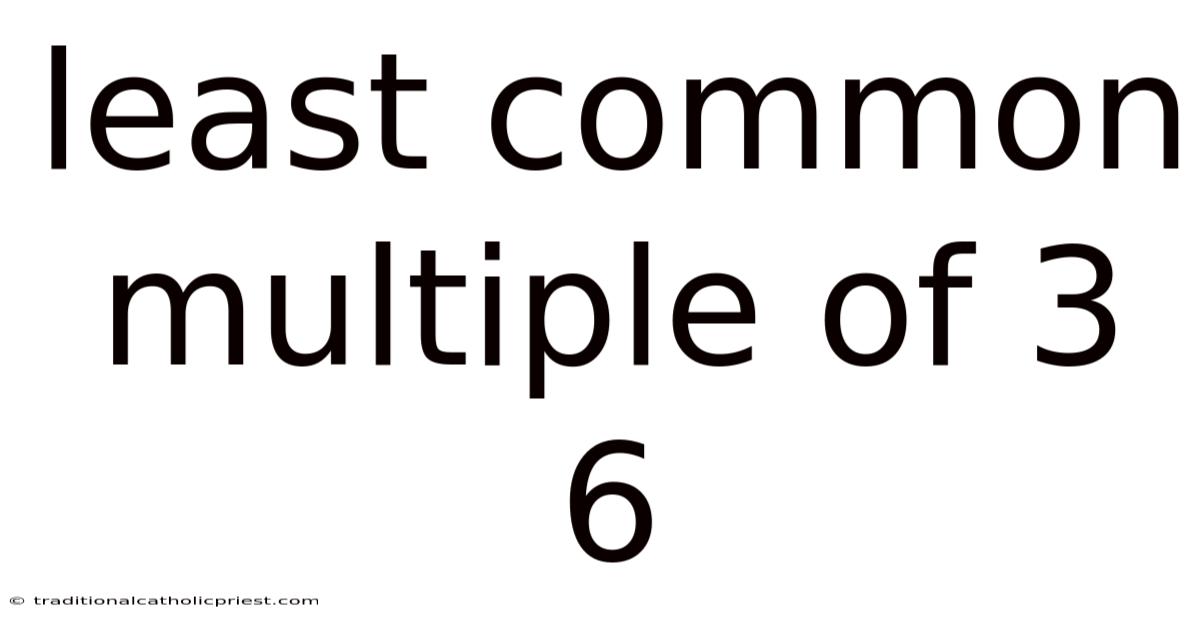
Table of Contents
Imagine you're organizing a school event with two different activity stations. One station needs volunteers every 3 hours, while the other needs them every 6 hours. You want to figure out when both stations will need volunteers at the same time so you can plan effectively. This is where the concept of the least common multiple comes into play.
In mathematics, the least common multiple (LCM) is a foundational concept with broad applications. It's the smallest positive integer that is perfectly divisible by two or more numbers. Understanding and calculating the LCM is crucial not only for solving mathematical problems but also for real-world applications. In this article, we will delve into the specifics of finding the least common multiple of 3 and 6, exploring various methods, practical applications, and expert tips to solidify your understanding.
Understanding the Least Common Multiple
The least common multiple, or LCM, is a fundamental concept in number theory. It helps simplify complex mathematical problems and is particularly useful in everyday situations requiring synchronization or scheduling.
At its core, the LCM of two or more numbers is the smallest number that is a multiple of each of the given numbers. In simpler terms, it’s the smallest number that each of the given numbers can divide into without leaving a remainder. For instance, if you are looking for the LCM of 4 and 6, you are seeking the smallest number that both 4 and 6 can divide into evenly. That number is 12.
Mathematical Definition
Mathematically, the LCM of two integers a and b is denoted as LCM(a, b). It is the smallest positive integer m such that a divides m and b divides m. This can be formally written as:
- a | m (which means a is a divisor of m)
- b | m (which means b is a divisor of m)
Historical Context
The concept of the LCM has ancient roots, tracing back to early civilizations that needed to solve problems related to time measurement, trade, and construction. Ancient mathematicians in Mesopotamia and Egypt used the LCM to synchronize calendars and manage trade cycles. The formalization of the concept, however, came later with the development of number theory in Greek mathematics, particularly through the works of Euclid. Euclid's Elements provides some of the earliest known methods for finding the LCM, closely linked with finding the greatest common divisor (GCD).
Why is LCM Important?
Understanding the LCM is vital for several reasons:
- Simplifying Fractions: The LCM is used to find the least common denominator when adding or subtracting fractions, making the process much simpler.
- Solving Algebraic Equations: In algebra, the LCM is crucial for simplifying expressions and solving equations involving fractions.
- Scheduling and Synchronization: In real-world applications, the LCM is used to solve scheduling problems, such as determining when events will coincide.
- Engineering and Computer Science: The LCM appears in various algorithms and system designs, particularly those involving periodic events or resource allocation.
Comprehensive Overview: Finding the LCM of 3 and 6
Now, let's focus specifically on finding the least common multiple of 3 and 6. We’ll explore several methods to illustrate how the LCM is derived and to ensure you have a solid understanding of the process.
Method 1: Listing Multiples
One of the most straightforward methods to find the LCM of two numbers is by listing their multiples until a common multiple is found.
- List Multiples of 3:
- 3, 6, 9, 12, 15, 18, ...
- List Multiples of 6:
- 6, 12, 18, 24, 30, ...
By comparing the lists, you can see that the smallest multiple common to both 3 and 6 is 6. Therefore, the LCM(3, 6) = 6.
Method 2: Prime Factorization
The prime factorization method involves breaking down each number into its prime factors and then using these factors to find the LCM.
- Prime Factorization of 3:
- 3 = 3
- Prime Factorization of 6:
- 6 = 2 × 3
To find the LCM, take the highest power of each prime factor that appears in either factorization:
- Prime factor 2 appears with a power of 1 (in the factorization of 6).
- Prime factor 3 appears with a power of 1 (in both factorizations).
Thus, LCM(3, 6) = 2¹ × 3¹ = 2 × 3 = 6.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM can also be found using the relationship between the LCM and the greatest common divisor (GCD). The formula is:
LCM(a, b) = (|a × b|) / GCD(a, b)
- Find the GCD of 3 and 6:
- The factors of 3 are 1 and 3.
- The factors of 6 are 1, 2, 3, and 6.
- The greatest common divisor is 3.
- Apply the Formula:
- LCM(3, 6) = (|3 × 6|) / 3 = 18 / 3 = 6.
Comparative Analysis
Each method provides a way to find the LCM of 3 and 6, but they vary in efficiency and suitability depending on the numbers involved:
- Listing Multiples: Simple for small numbers but becomes cumbersome for larger numbers.
- Prime Factorization: Efficient and reliable, especially for larger numbers, but requires knowledge of prime factorization.
- Using GCD: Requires finding the GCD first, which might be more complex for some numbers but can be efficient if the GCD is easily determined.
In the case of 3 and 6, all three methods are relatively straightforward and yield the same result: the LCM of 3 and 6 is 6.
Trends and Latest Developments
While the concept of the LCM has been around for centuries, its applications continue to evolve with advancements in technology and computational mathematics. Here are some trends and developments related to the LCM:
Computational Tools and Algorithms
Modern computational tools and algorithms have made it easier to compute the LCM of large numbers and sets of numbers. Software like Mathematica, MATLAB, and Python libraries offer built-in functions to compute the LCM efficiently. These tools are crucial in fields like cryptography, where large numbers are frequently used.
Real-World Data Applications
- Supply Chain Management: Companies use LCM to synchronize deliveries and optimize inventory levels. For example, if one supplier delivers every 3 days and another every 6 days, knowing the LCM helps in planning warehouse space and coordinating logistics.
- Healthcare Scheduling: Hospitals use LCM to schedule periodic maintenance of equipment and coordinate staff rotations to ensure optimal resource allocation.
- Telecommunications: In telecommunications, the LCM is used to synchronize data transmission and network maintenance schedules to minimize downtime.
Educational Trends
Educational approaches are also evolving to make the concept of the LCM more accessible and engaging for students. Interactive software, online games, and real-world problem-solving activities are increasingly used to teach the LCM. These methods help students grasp the practical relevance of the LCM, making learning more effective and enjoyable.
Expert Insights
According to Dr. Emily Carter, a professor of mathematics at MIT, "Understanding the LCM is not just about performing calculations; it's about developing a deeper understanding of number theory and its applications. The LCM is a foundational concept that supports more advanced topics in mathematics and computer science."
Additionally, the rise of big data and analytics has increased the demand for professionals who can apply mathematical concepts like the LCM to solve complex real-world problems. Data scientists and analysts use the LCM to optimize algorithms, streamline processes, and make data-driven decisions.
Tips and Expert Advice
To master the concept of the least common multiple of 3 and 6 and similar problems, consider these tips and expert advice:
Tip 1: Practice Regularly
Consistent practice is key to mastering any mathematical concept. Start with simple problems and gradually work your way up to more complex ones. Use online resources, textbooks, and worksheets to practice finding the LCM of different sets of numbers.
Example: Find the LCM of 2 and 4, 3 and 9, and 5 and 10. Regular practice will help you quickly recognize common multiples and apply the appropriate methods.
Tip 2: Understand the Underlying Concepts
Don't just memorize the formulas; understand the underlying concepts. Know why the LCM is useful and how it relates to other mathematical concepts like the greatest common divisor (GCD).
Explanation: Understanding that the LCM is the smallest number divisible by all given numbers helps you approach problems more intuitively. This understanding makes it easier to choose the most efficient method for finding the LCM.
Tip 3: Use Visual Aids
Visual aids like number lines, Venn diagrams, and charts can help you visualize the multiples and factors of numbers. This can be particularly useful for students who are visual learners.
Example: Create a Venn diagram with the multiples of 3 in one circle and the multiples of 6 in another. The overlapping region will contain the common multiples, and the smallest number in this region is the LCM.
Tip 4: Apply Real-World Problems
Applying the LCM to real-world problems can make the concept more relatable and engaging. Look for opportunities to use the LCM in everyday situations, such as scheduling events, managing time, or optimizing resources.
Example: If you need to schedule two tasks, one that needs to be done every 3 days and another every 6 days, use the LCM to determine when both tasks will need to be done on the same day. This helps you plan your schedule efficiently.
Tip 5: Master Prime Factorization
Prime factorization is a powerful tool for finding the LCM of larger numbers. Invest time in mastering prime factorization techniques, as it will make finding the LCM much easier.
Explanation: Being able to quickly break down numbers into their prime factors allows you to efficiently identify the highest powers of each prime factor and calculate the LCM accurately.
Expert Advice from Educators
According to math educators, teaching the LCM effectively involves connecting the concept to real-world applications and using a variety of teaching methods to cater to different learning styles. Incorporating group activities, games, and technology can also enhance students' understanding and engagement.
FAQ
Q: What is the LCM of 3 and 6?
A: The LCM of 3 and 6 is 6.
Q: How do you find the LCM of 3 and 6 using the listing method?
A: List the multiples of 3 (3, 6, 9, ...) and the multiples of 6 (6, 12, 18, ...). The smallest common multiple is 6.
Q: How do you find the LCM of 3 and 6 using prime factorization?
A: The prime factorization of 3 is 3, and the prime factorization of 6 is 2 × 3. Take the highest power of each prime factor: 2¹ × 3¹ = 6.
Q: Can the LCM be smaller than the numbers themselves?
A: No, the LCM is always greater than or equal to the largest of the numbers.
Q: Why is the LCM important in everyday life?
A: The LCM is used for scheduling, synchronizing events, simplifying fractions, and solving problems related to resource allocation.
Q: Is there a formula to find the LCM?
A: Yes, LCM(a, b) = (|a × b|) / GCD(a, b), where GCD is the greatest common divisor.
Conclusion
In summary, the least common multiple of 3 and 6 is 6. This fundamental concept has wide-ranging applications in mathematics, science, and everyday life. Whether you are simplifying fractions, scheduling events, or optimizing resources, understanding the LCM is essential. By using methods like listing multiples, prime factorization, and the GCD formula, you can confidently solve LCM problems.
Now that you have a comprehensive understanding of the LCM, put your knowledge into practice. Solve more problems, explore real-world applications, and share your insights with others. Dive deeper into related mathematical concepts to further enhance your skills. The journey to mastering mathematics is continuous, and every step you take brings you closer to unlocking its full potential.
Latest Posts
Latest Posts
-
Does Soh Cah Toa Only Work On Right Triangles
Nov 17, 2025
-
How Many Capacitors Are In An Ac Unit
Nov 17, 2025
-
How To Find X In Triangle
Nov 17, 2025
-
Can You Bring Mangoes From Mexico To Us
Nov 17, 2025
-
What Are The Factors For 77
Nov 17, 2025
Related Post
Thank you for visiting our website which covers about Least Common Multiple Of 3 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.