Is 5 8 Less Than 3 4
catholicpriest
Nov 14, 2025 · 13 min read
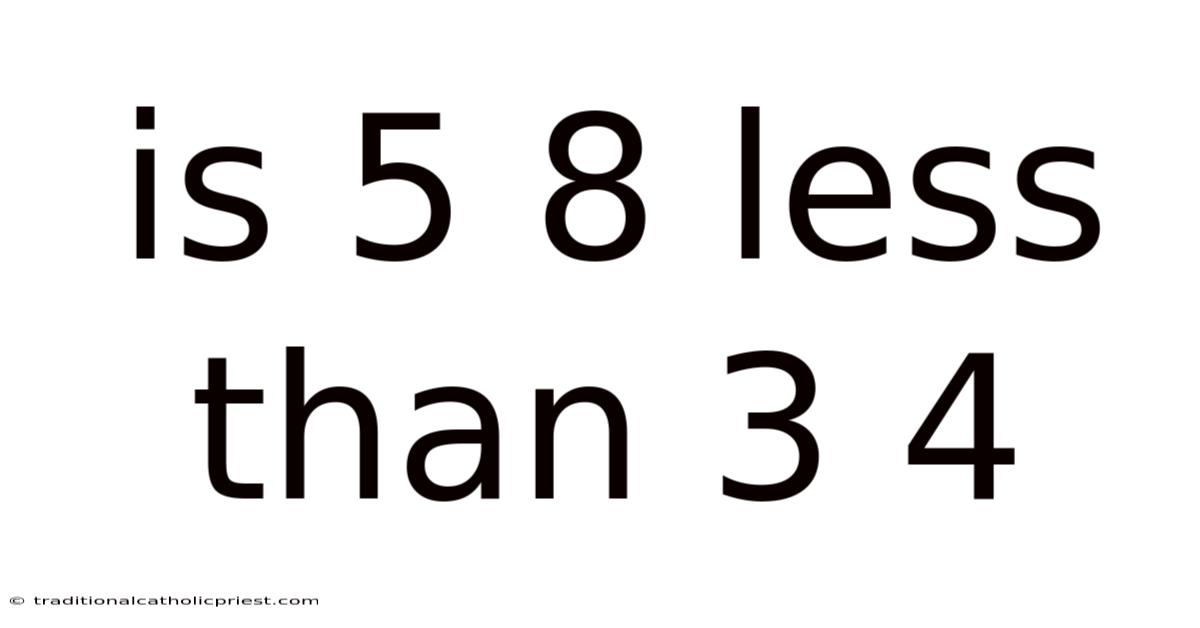
Table of Contents
Imagine you're baking a pie. The recipe calls for fractions of ingredients, and you need to figure out if you have enough flour. You have 5/8 of a cup, but the recipe needs 3/4 of a cup. Do you need to run to the store, or are you all set? Understanding how to compare fractions is crucial in many everyday situations, from cooking to managing finances. Let's dive into comparing 5/8 and 3/4 to see which is larger and explore the different methods we can use.
Comparing fractions like 5/8 and 3/4 might seem daunting at first, but it's a fundamental skill that simplifies many aspects of life. Whether you're a student learning fractions for the first time or someone who wants to brush up on your math skills, knowing how to compare fractions accurately is incredibly useful. In this comprehensive guide, we will explore various methods to determine if 5/8 is less than 3/4, providing step-by-step explanations and practical tips along the way. We will also look at real-world applications and address some frequently asked questions to ensure you have a solid understanding of this topic. So, is 5/8 less than 3/4? Let's find out!
Main Subheading
The ability to compare fractions is a fundamental concept in mathematics, critical for problem-solving in various contexts. Fractions represent parts of a whole, and comparing them allows us to determine which part is larger or smaller. Understanding this concept is essential not only for academic purposes but also for practical, everyday applications such as cooking, measuring, and financial calculations. In the case of 5/8 and 3/4, we are essentially asking whether five-eighths of something is less than three-quarters of the same thing.
To accurately compare these fractions, we need to delve into several methods that provide clear and understandable comparisons. These methods include finding common denominators, converting fractions to decimals, and using visual aids. Each method offers a unique approach to understanding the relative sizes of fractions. By exploring these methods, we can confidently determine which fraction is larger and apply this knowledge to solve similar problems in the future. Whether you're a student, a professional, or simply someone looking to improve your math skills, mastering the comparison of fractions is a valuable asset.
Comprehensive Overview
To determine whether 5/8 is less than 3/4, we can explore several methods, each providing a unique perspective on the comparison. These methods include:
- Finding a Common Denominator
- Converting to Decimals
- Using Visual Aids
Finding a Common Denominator
The most common and reliable method for comparing fractions is to find a common denominator. The denominator is the bottom number of a fraction, representing the total number of parts the whole is divided into. To compare fractions, they must have the same denominator, allowing us to directly compare the numerators (the top numbers), which represent how many of those parts we have.
To find a common denominator for 5/8 and 3/4, we need to identify the least common multiple (LCM) of the denominators 8 and 4. The multiples of 8 are 8, 16, 24, and so on, while the multiples of 4 are 4, 8, 12, 16, and so on. The LCM of 8 and 4 is 8. This means we can easily convert both fractions to have a denominator of 8.
The fraction 5/8 already has the desired denominator. To convert 3/4 to a fraction with a denominator of 8, we multiply both the numerator and the denominator by the same number so that the denominator becomes 8. In this case, we multiply both by 2: (3 * 2) / (4 * 2) = 6/8 Now we can easily compare the two fractions: 5/8 and 6/8. Since 5 is less than 6, we can conclude that 5/8 is less than 6/8. Therefore, 5/8 is less than 3/4.
Converting to Decimals
Another straightforward method for comparing fractions is to convert them to decimals. This involves dividing the numerator by the denominator. Once both fractions are in decimal form, comparing them is as simple as comparing decimal numbers.
To convert 5/8 to a decimal, we divide 5 by 8: 5 ÷ 8 = 0.625 To convert 3/4 to a decimal, we divide 3 by 4: 3 ÷ 4 = 0.75 Now we compare the two decimals: 0.625 and 0.75. Since 0.625 is less than 0.75, we can conclude that 5/8 is less than 3/4.
Using Visual Aids
Visual aids, such as diagrams or number lines, can be incredibly helpful for understanding and comparing fractions, especially for visual learners. These tools provide a concrete representation of fractions, making it easier to see their relative sizes.
Diagrams: Imagine two identical rectangles. Divide the first rectangle into 8 equal parts and shade 5 of those parts to represent 5/8. Divide the second rectangle into 4 equal parts and shade 3 of those parts to represent 3/4. By visually comparing the shaded areas, you can see that the area representing 3/4 is larger than the area representing 5/8.
Number Lines: Draw a number line from 0 to 1. Divide the number line into intervals representing eighths (1/8, 2/8, 3/8, and so on) and fourths (1/4, 2/4, 3/4, and so on). Plot the points 5/8 and 3/4 on the number line. By observing the positions of these points, you can see that 5/8 is to the left of 3/4, indicating that 5/8 is less than 3/4.
Each of these methods provides a clear way to compare fractions. Whether you prefer finding common denominators, converting to decimals, or using visual aids, the key is to choose the method that you find most intuitive and easy to understand. By mastering these techniques, you'll be able to confidently compare any fractions and apply this skill in various real-world scenarios.
Trends and Latest Developments
In recent years, there has been an increasing emphasis on practical math skills, particularly in elementary and middle school education. Educators and curriculum developers are focusing on teaching fractions in a way that connects to real-life situations, making the concept more relatable and easier to grasp for students. This trend is driven by the understanding that a solid foundation in fractions is crucial for success in higher-level math courses and in various STEM fields.
One notable trend is the use of technology in teaching fractions. Interactive apps, online games, and educational websites offer engaging ways for students to practice comparing fractions. These tools often provide immediate feedback and personalized learning experiences, helping students to identify and address their specific areas of difficulty. For example, some apps use visual models to help students understand the concept of equivalent fractions, while others offer timed quizzes to improve their speed and accuracy in comparing fractions.
Another development is the focus on conceptual understanding rather than rote memorization. Educators are encouraging students to explore the underlying principles of fractions through hands-on activities and real-world examples. This approach helps students to develop a deeper understanding of fractions and to apply their knowledge in a variety of contexts. For instance, students might use measuring cups to compare fractions of water or cut pizzas into slices to understand the concept of equivalent fractions.
Data from educational research consistently shows that students who have a strong understanding of fractions perform better in algebra and other advanced math courses. As a result, there is a growing recognition of the importance of early intervention for students who struggle with fractions. Many schools are implementing targeted interventions to provide additional support to these students, helping them to catch up and build a solid foundation in fractions. These interventions often involve small-group instruction, one-on-one tutoring, and the use of manipulatives to make the concept more concrete.
Professional insights from math educators highlight the importance of making fractions relevant to students' lives. By connecting fractions to real-world situations, educators can help students to see the value of learning this concept. For example, students might use fractions to calculate discounts while shopping, to determine the amount of ingredients needed for a recipe, or to understand the proportions in a scale model. This approach not only makes fractions more engaging but also helps students to develop problem-solving skills that are essential for success in the 21st century.
Tips and Expert Advice
Comparing fractions can be straightforward if you use the right strategies. Here are some expert tips and practical advice to help you master this skill:
Simplify Fractions First
Before comparing fractions, always check if they can be simplified. Simplifying fractions makes the numbers smaller and easier to work with, reducing the chances of making errors. To simplify a fraction, find the greatest common factor (GCF) of the numerator and the denominator and divide both by that number.
For example, if you were comparing 4/8 and 3/4, you could simplify 4/8 to 1/2 by dividing both the numerator and denominator by 4. Now, comparing 1/2 and 3/4 is much easier. You can quickly convert 1/2 to 2/4 and see that 2/4 is less than 3/4. This simple step can save time and effort.
Use Benchmarks
Benchmarks are common fractions that you can use as reference points when comparing other fractions. Common benchmarks include 0, 1/2, and 1. If a fraction is less than 1/2 and another is greater than 1/2, you immediately know which one is smaller without doing any complex calculations.
For instance, consider comparing 2/5 and 5/8. You know that 2/5 is less than 1/2 (since 2.5/5 would be 1/2) and 5/8 is greater than 1/2 (since 4/8 would be 1/2). Therefore, 2/5 is less than 5/8. Using benchmarks can provide a quick and easy way to compare fractions without needing to find common denominators or convert to decimals.
Cross-Multiplication
Cross-multiplication is a quick method for comparing two fractions. To use this method, multiply the numerator of the first fraction by the denominator of the second fraction, and then multiply the numerator of the second fraction by the denominator of the first fraction. Compare the two products. If the first product is smaller, then the first fraction is smaller. If the second product is smaller, then the second fraction is smaller.
For example, to compare 5/8 and 3/4 using cross-multiplication, multiply 5 by 4 (which equals 20) and multiply 3 by 8 (which equals 24). Since 20 is less than 24, 5/8 is less than 3/4. This method is particularly useful when dealing with fractions that are difficult to convert to a common denominator or decimals.
Practice Regularly
Like any skill, mastering the comparison of fractions requires practice. The more you practice, the more comfortable and confident you will become. Try solving a variety of problems involving different types of fractions, including proper fractions, improper fractions, and mixed numbers.
You can find practice problems in textbooks, online resources, or educational apps. Consider creating your own practice problems as well. Regular practice will help you to internalize the different methods and strategies for comparing fractions, making it easier to apply them in real-world situations.
Use Real-World Examples
Connecting fractions to real-world examples can make the concept more meaningful and easier to understand. Think about situations where you might need to compare fractions, such as cooking, measuring, or sharing items.
For example, if you are following a recipe that calls for 2/3 cup of flour and you only have 3/5 cup, you can compare these fractions to determine if you have enough flour. Or, if you are sharing a pizza with friends and you want to make sure everyone gets a fair share, you can use fractions to divide the pizza equally. By relating fractions to real-world scenarios, you can develop a deeper understanding of their practical applications.
Seek Help When Needed
If you are struggling with comparing fractions, don't hesitate to seek help from teachers, tutors, or online resources. Sometimes, a different explanation or a fresh perspective can make all the difference.
Teachers and tutors can provide personalized instruction and address your specific areas of difficulty. Online resources, such as educational websites and videos, can offer additional explanations and examples. Don't be afraid to ask questions and seek clarification until you fully understand the concept.
By following these tips and expert advice, you can improve your skills in comparing fractions and confidently apply this knowledge in various contexts. Remember to simplify fractions, use benchmarks, cross-multiply, practice regularly, use real-world examples, and seek help when needed. With dedication and effort, you can master the comparison of fractions and unlock a valuable tool for problem-solving and decision-making.
FAQ
Q: Why is finding a common denominator important when comparing fractions? A: Finding a common denominator allows you to compare fractions directly because it ensures that you are comparing parts of the same whole. When fractions have the same denominator, the numerators can be directly compared to determine which fraction represents a larger portion.
Q: Can I always use cross-multiplication to compare fractions? A: Yes, cross-multiplication is a reliable method for comparing any two fractions. By multiplying the numerator of one fraction by the denominator of the other and comparing the results, you can quickly determine which fraction is larger or smaller.
Q: Is converting fractions to decimals always the best method for comparison? A: Converting to decimals is a straightforward method, but it may not always be the most efficient, especially for fractions that result in repeating decimals. However, for most practical purposes, it is a reliable and easy-to-understand method.
Q: What are some common mistakes to avoid when comparing fractions? A: Common mistakes include forgetting to find a common denominator, incorrectly converting fractions to decimals, and not simplifying fractions before comparing them. Always double-check your work to avoid these errors.
Q: How can I help my child understand how to compare fractions? A: Use visual aids like diagrams and number lines, relate fractions to real-world examples, and provide plenty of practice opportunities. Make it fun and engaging to help them develop a solid understanding of the concept.
Conclusion
In summary, determining whether 5/8 is less than 3/4 involves using methods such as finding common denominators, converting to decimals, or employing visual aids. Through these approaches, it becomes clear that 5/8 is indeed less than 3/4. Mastering the skill of comparing fractions is essential for both academic and real-world applications, enabling more accurate calculations and better decision-making.
To further enhance your understanding and skills, practice regularly with different types of fractions and explore real-world scenarios where comparing fractions is necessary. Whether you're baking, measuring, or managing finances, the ability to confidently compare fractions will prove invaluable.
Now that you've gained a solid understanding of how to compare fractions, take the next step and apply this knowledge to solve practical problems. Share your experiences and insights in the comments below, and encourage others to explore the fascinating world of fractions!
Latest Posts
Latest Posts
-
Compare And Contrast A Food Chain And A Food Web
Nov 14, 2025
-
What Is Difference Between Evaporation And Boiling
Nov 14, 2025
-
Is Carbon Dioxide A Covalent Bond
Nov 14, 2025
-
What Is The Meaning Of The Suffix Ness
Nov 14, 2025
-
The Corpus Callosum Is Composed Of
Nov 14, 2025
Related Post
Thank you for visiting our website which covers about Is 5 8 Less Than 3 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.