Is 5 2 Greater Than 1
catholicpriest
Nov 08, 2025 · 12 min read
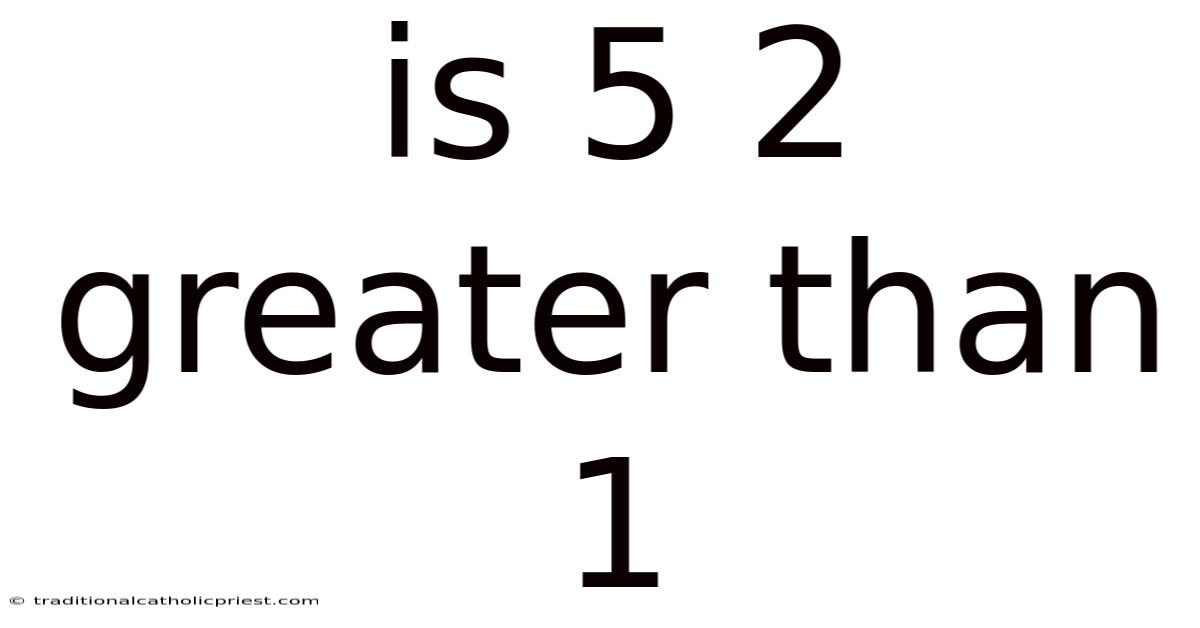
Table of Contents
Imagine you're at a bustling farmer's market, deciding between a vibrant basket of five ripe apples and just one enormous, prize-winning pumpkin. Numerically, five is undeniably larger than one. But what if that single pumpkin is so massive it outweighs all the apples combined? This seemingly simple comparison highlights a concept we often take for granted: the value and context behind the numbers themselves.
At first glance, the statement "5 2 greater than 1" seems incomplete, even nonsensical. What does the '2' signify in this context? The answer lies in understanding mathematical notation and the power of exponents. When we write 5², we're not simply looking at the number 5 beside the number 2; instead, we are performing the operation of squaring 5, meaning we multiply 5 by itself. Therefore, the question we're truly asking is whether 5 squared is greater than 1. Spoiler alert: it is. But delving deeper into the logic behind this seemingly simple problem allows us to explore fundamental mathematical principles and appreciate the elegance of numerical relationships.
Main Subheading
Understanding Exponents and Mathematical Notation
To accurately assess whether 5² is greater than 1, we must first understand the concept of exponents and how they function within mathematical notation. Exponents provide a concise way to represent repeated multiplication. Instead of writing 5 * 5, we can simply write 5², where 5 is the base and 2 is the exponent. The exponent indicates how many times the base is multiplied by itself.
The history of exponents can be traced back to ancient civilizations. Early forms of mathematical notation used cumbersome methods for representing repeated multiplication. Over time, mathematicians sought more efficient and symbolic ways to express these concepts. The modern notation we use today evolved gradually, with contributions from various mathematicians across different eras. For example, René Descartes is often credited with standardizing the use of superscripts to denote exponents in the 17th century. The development of exponential notation was crucial for advancements in algebra, calculus, and various scientific fields. It allowed for more complex equations and models to be expressed and manipulated with greater ease.
Comprehensive Overview
The Mathematics Behind the Comparison
In our case, 5² means 5 multiplied by itself: 5 * 5. This calculation yields 25. Now, the comparison becomes straightforward: is 25 greater than 1? The answer is unequivocally yes. This example illustrates a fundamental principle: when a number greater than 1 is raised to a positive integer exponent, the result will always be greater than the original number and, consequently, greater than 1.
To solidify this understanding, let's consider a few more examples:
- 3² = 3 * 3 = 9, which is greater than 1.
- 10² = 10 * 10 = 100, which is greater than 1.
- 2³ = 2 * 2 * 2 = 8, which is greater than 1.
These examples demonstrate that exponents amplify the value of the base number. However, there are exceptions to this general rule. If the base number is between 0 and 1, raising it to a positive exponent will result in a smaller number. For example:
- (0.5)² = 0.5 * 0.5 = 0.25, which is less than 1.
- (0.1)² = 0.1 * 0.1 = 0.01, which is less than 1.
Furthermore, any number raised to the power of 0 equals 1 (except for 0 itself, which is undefined). And any number raised to the power of 1 equals itself. These are important cornerstones to understanding exponential rules and calculations.
Practical Applications of Exponents
Exponents are not merely abstract mathematical concepts; they have widespread applications in various fields, including science, engineering, finance, and computer science. For example:
- Science: Exponents are used to express very large or very small numbers in scientific notation. For instance, the speed of light is approximately 3 x 10⁸ meters per second. Exponents also appear in formulas describing exponential growth and decay, such as radioactive decay or population growth.
- Engineering: Exponents are crucial in calculating areas, volumes, and other geometric properties. For example, the area of a square is calculated by squaring the length of one side (side²), and the volume of a cube is calculated by cubing the length of one side (side³).
- Finance: Compound interest is a prime example of exponential growth. The future value of an investment grows exponentially as interest is earned on both the principal and accumulated interest.
- Computer Science: Exponents are fundamental in computer science, particularly in the representation of data and the analysis of algorithms. The number of bits required to represent a certain range of numbers grows logarithmically, which is the inverse of exponential growth. Algorithm complexity is often expressed using big O notation, which involves exponents to describe how the runtime of an algorithm scales with the size of the input.
- Cryptography: Exponential functions are widely used in cryptography to create secure encryption algorithms. The difficulty of breaking these algorithms relies on the computational complexity of reversing exponential operations, such as discrete logarithms.
Common Misconceptions about Exponents
Despite their widespread use, exponents are often misunderstood. One common misconception is confusing exponents with multiplication. For instance, some might incorrectly assume that 5² is equal to 5 * 2, which is 10, rather than the correct answer of 25. It is crucial to remember that exponents represent repeated multiplication, not simple multiplication by the exponent itself.
Another misconception involves negative exponents. A negative exponent indicates the reciprocal of the base raised to the positive value of the exponent. For example, 5⁻² is equal to 1 / 5², which is 1 / 25 or 0.04.
Fractional exponents are also frequently misunderstood. A fractional exponent represents a root. For example, 5¹/² is equal to the square root of 5. The denominator of the fraction indicates the type of root (2 for square root, 3 for cube root, and so on).
Finally, it's important to distinguish between exponents and indices. While the terms are sometimes used interchangeably, indices generally refer to subscripts used to label elements in a sequence or array, whereas exponents specifically denote the power to which a number is raised.
The Significance of Numerical Comparisons
The simple comparison of 5² to 1 underscores the importance of numerical comparisons in mathematics and everyday life. Numerical comparisons allow us to quantify relationships, make informed decisions, and solve problems. Whether we are comparing prices at the grocery store, analyzing data in a scientific experiment, or evaluating financial investments, the ability to compare numbers accurately is essential.
Understanding mathematical concepts like exponents and being able to perform numerical comparisons provides a foundation for critical thinking and problem-solving skills. It enables us to analyze information, identify patterns, and draw logical conclusions. In an increasingly data-driven world, these skills are more valuable than ever.
Trends and Latest Developments
Recent Advancements in Exponential Calculations
While the basic principles of exponents remain unchanged, advancements in computer technology and algorithms have revolutionized how we perform complex exponential calculations. Modern computers can handle exponential calculations with incredible speed and precision, enabling scientists and engineers to solve problems that were previously intractable.
One area of active research is the development of more efficient algorithms for modular exponentiation, which is used extensively in cryptography. These algorithms aim to reduce the computational cost of raising large numbers to large powers modulo a prime number, thereby improving the performance of encryption and decryption processes.
Another trend is the use of parallel computing to accelerate exponential calculations. By distributing the computational workload across multiple processors, it is possible to perform exponential calculations on extremely large numbers in a fraction of the time. This is particularly relevant in fields such as number theory and cryptography, where computations often involve numbers with hundreds or thousands of digits.
Popular Opinions and Discussions
The concept of exponents, while fundamental, often sparks interesting discussions among mathematics enthusiasts and educators. One recurring topic is the best way to teach exponents to students. Some advocate for a hands-on approach, using concrete examples and manipulatives to illustrate the concept of repeated multiplication. Others emphasize the importance of understanding the underlying mathematical principles and developing a strong foundation in algebra.
Another popular discussion revolves around the role of calculators and computers in mathematics education. While calculators can be useful for performing complex calculations, some argue that over-reliance on calculators can hinder students' understanding of fundamental concepts. It is important to strike a balance between using technology as a tool and developing strong mental math skills.
Furthermore, the applications of exponential functions in various fields often generate interest and debate. For example, the use of exponential models to predict the spread of infectious diseases has been a topic of intense discussion during the COVID-19 pandemic. Understanding the limitations of these models and the factors that can influence their accuracy is crucial for making informed public health decisions.
Tips and Expert Advice
Mastering Exponents: Practical Tips
To truly master exponents, practice is key. Work through a variety of problems, starting with simple examples and gradually increasing in complexity. Pay close attention to the order of operations and remember the rules for dealing with negative and fractional exponents.
- Start with the basics: Ensure you have a solid understanding of the definition of exponents and how they represent repeated multiplication.
- Practice regularly: Consistent practice is essential for reinforcing your understanding and developing fluency.
- Use visual aids: Visual aids, such as diagrams or charts, can help you visualize the concept of exponents and how they affect the value of numbers.
- Work through examples: Work through a variety of examples, covering different types of exponents (positive, negative, fractional) and different bases.
- Solve problems step-by-step: Break down complex problems into smaller, more manageable steps. This will help you avoid errors and understand the reasoning behind each step.
Real-World Examples
Understanding exponents can be highly advantageous in various practical scenarios. Imagine you are planning a savings strategy with compound interest. The formula for compound interest involves exponents. If you invest a principal amount (P) at an annual interest rate (r) compounded (n) times per year for (t) years, the future value (A) of your investment is given by:
A = P (1 + r/n)^(nt)
The exponent (nt) significantly impacts the growth of your investment over time. A higher compounding frequency (n) leads to more frequent interest calculations, resulting in faster growth due to the effect of the exponent.
Another example lies in understanding the processing power of computers. Computer processing power is often measured in terms of bits and bytes, which are based on powers of 2. For example, a kilobyte (KB) is 2¹⁰ bytes, a megabyte (MB) is 2²⁰ bytes, and a gigabyte (GB) is 2³⁰ bytes. Understanding these exponential relationships can help you appreciate the rapid advancements in computer technology and the increasing storage capacity of modern devices.
Furthermore, exponents play a crucial role in calculating the area and volume of geometric shapes. For example, if you are designing a garden, the area you have to work with will likely determine the amount of plants you can fit. Squaring the dimensions of a square or cubing the dimensions of a cube utilizes the exponential concept.
Common Mistakes to Avoid
When working with exponents, it's easy to make mistakes if you're not careful. One common mistake is confusing exponents with multiplication. Remember that 5² means 5 * 5, not 5 * 2.
Another common mistake is mishandling negative exponents. A negative exponent indicates the reciprocal of the base raised to the positive value of the exponent. For example, 5⁻² is equal to 1 / 5², which is 1 / 25 or 0.04.
When dealing with fractional exponents, remember that they represent roots. For example, 5¹/² is equal to the square root of 5. The denominator of the fraction indicates the type of root (2 for square root, 3 for cube root, and so on).
Resources for Further Learning
There are many excellent resources available for learning more about exponents. Textbooks, online courses, and educational websites offer comprehensive explanations and practice problems. Some popular resources include:
- Khan Academy: Khan Academy offers free video tutorials and practice exercises on a wide range of math topics, including exponents.
- Mathway: Mathway is an online calculator that can solve complex math problems, including those involving exponents. It also provides step-by-step explanations of the solutions.
- Wolfram Alpha: Wolfram Alpha is a computational knowledge engine that can perform complex calculations and provide detailed information on a wide range of topics, including mathematics.
- Your local library: Your local library has a wealth of books and other resources on mathematics, including textbooks and study guides.
FAQ
Is 0 raised to the power of 0 equal to 1?
Technically, 0⁰ is generally considered undefined in many contexts. While some areas of mathematics define it as 1 for convenience (particularly in combinatorics), it's best to avoid using it without a clear understanding of the specific mathematical context.
What is a fractional exponent?
A fractional exponent represents a root. For instance, x^(1/n) is the nth root of x. For example, 9^(1/2) is the square root of 9, which equals 3.
How do you simplify expressions with exponents?
Use the rules of exponents:
- xᵃ * xᵇ = xᵃ⁺ᵇ
- xᵃ / xᵇ = xᵃ⁻ᵇ
- (xᵃ)ᵇ = xᵃᵇ
- (xy)ᵃ = xᵃyᵃ
- (x/y)ᵃ = xᵃ/yᵃ
What is the difference between an exponent and a logarithm?
Exponents and logarithms are inverse operations. If y = bˣ, then log_b(y) = x. The logarithm answers the question, "To what power must we raise the base b to get y?".
Can exponents be negative?
Yes, negative exponents represent reciprocals. x⁻ᵃ = 1 / xᵃ. For example, 2⁻² = 1 / 2² = 1/4.
Conclusion
In summary, 5² is indeed greater than 1. This simple mathematical comparison allows us to explore the power of exponents and their profound impact on various fields, from science and engineering to finance and computer science. Understanding exponents and numerical comparisons provides a foundation for critical thinking and problem-solving skills in an increasingly data-driven world.
Now that you have a solid understanding of exponents, why not put your knowledge to the test? Try solving some practice problems, explore real-world applications, and delve deeper into the fascinating world of mathematics. Share this article to spark curiosity in others and encourage them to embrace the power of numbers. What are your favorite examples of exponential growth or decay in the real world? Share your thoughts and questions in the comments below!
Latest Posts
Latest Posts
-
How To Find The Least Common Denominator In Fractions
Nov 08, 2025
-
Seven Letter Words Starting With O
Nov 08, 2025
-
Dissolved Oxygen And Biological Oxygen Demand
Nov 08, 2025
-
Mnemonic For Bones Of The Skull
Nov 08, 2025
-
Five Letter Words Ending In Id
Nov 08, 2025
Related Post
Thank you for visiting our website which covers about Is 5 2 Greater Than 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.