Is 1 4 Bigger Than 3 8
catholicpriest
Nov 16, 2025 · 10 min read
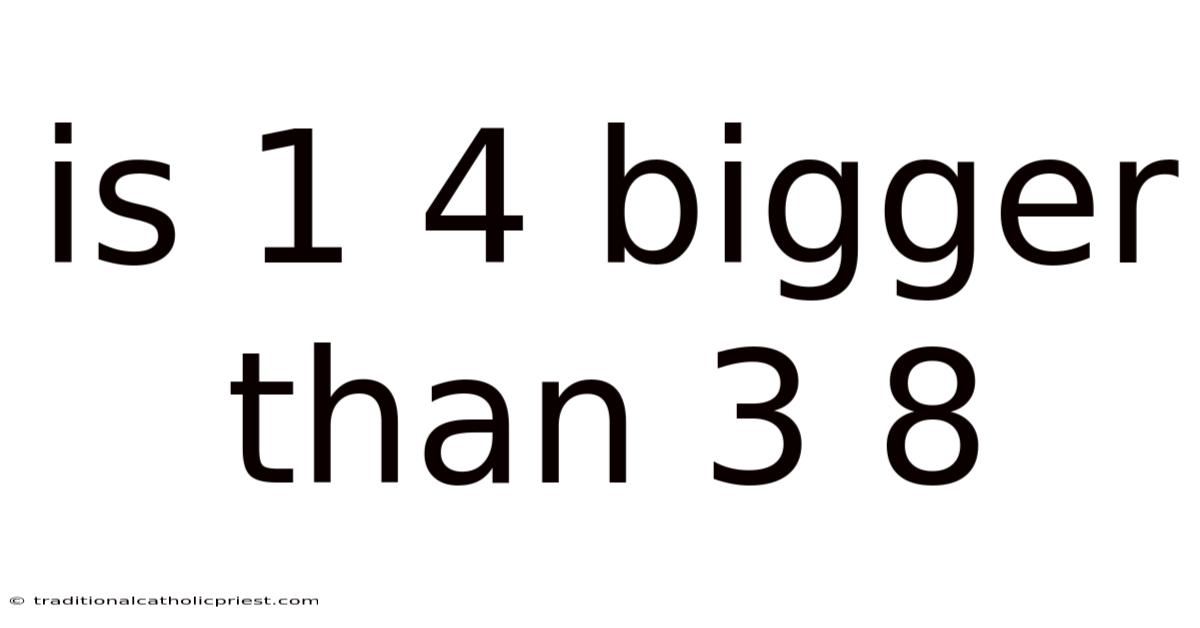
Table of Contents
Imagine you're baking a pizza with friends. You cut one pizza into four equal slices and grab one. Then, someone else cuts another pizza into eight slices and takes three. Who has more pizza? This simple scenario highlights the importance of understanding how to compare fractions, a fundamental skill in math that pops up in everyday life, from cooking to managing finances.
Comparing fractions might seem straightforward, but it involves understanding the relationships between numerators and denominators. When faced with fractions like 1/4 and 3/8, it's not immediately clear which is larger. This is where various methods of comparison come into play, helping us make accurate and informed decisions. So, is 1/4 bigger than 3/8? Let’s dive in and find out, exploring different techniques and real-world applications to make the concept clear and engaging.
Main Subheading
To properly answer the question "Is 1/4 bigger than 3/8?", we need to dive into the context of fractions and their comparison. Fractions represent parts of a whole, and comparing them involves determining which part is larger relative to that whole. This is a basic mathematical skill, but understanding the underlying principles is crucial for more complex math.
When comparing fractions, it's essential to consider both the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts of the whole we have, while the denominator indicates how many equal parts the whole is divided into. Simply looking at the numbers can be misleading; for example, 1/2 might seem smaller than 1/4 because 2 is smaller than 4, but in reality, 1/2 is much larger.
Comprehensive Overview
Defining Fractions
A fraction is a way to represent a part of a whole. It's written as a ratio of two numbers: the numerator and the denominator. The numerator tells you how many parts you have, and the denominator tells you how many parts the whole is divided into. For example, in the fraction 3/4, 3 is the numerator, and 4 is the denominator. This means you have 3 parts out of a total of 4 equal parts.
The Importance of Common Denominators
To accurately compare two or more fractions, they need to have a common denominator. This means that the denominators of all the fractions must be the same. When fractions have the same denominator, it becomes easy to compare them by simply looking at their numerators. The fraction with the larger numerator is the larger fraction. For example, comparing 2/5 and 4/5 is easy because they both have the same denominator (5). Since 4 is greater than 2, 4/5 is larger than 2/5.
Methods for Finding Common Denominators
- Finding the Least Common Multiple (LCM): The LCM is the smallest number that is a multiple of both denominators. This method is useful when the denominators are not easily related. For example, to compare 1/3 and 1/4, the LCM of 3 and 4 is 12.
- Multiplying Denominators: A simple way to find a common denominator is to multiply the two denominators together. While this method always works, it may not give you the least common denominator, which means you might have to simplify the fractions later. For example, to compare 1/2 and 1/3, you can multiply 2 and 3 to get a common denominator of 6.
- Identifying a Common Multiple: Sometimes, one denominator is a multiple of the other. In this case, you can use the larger denominator as the common denominator. For example, to compare 1/2 and 3/4, you can use 4 as the common denominator since 4 is a multiple of 2.
Converting Fractions to a Common Denominator
Once you've found a common denominator, you need to convert each fraction so that it has that denominator. To do this, you multiply both the numerator and the denominator of each fraction by the same number. This ensures that the value of the fraction remains unchanged. For example, to convert 1/2 to a fraction with a denominator of 4, you multiply both the numerator and the denominator by 2: (1 * 2) / (2 * 2) = 2/4.
Cross-Multiplication
Cross-multiplication is a quick method to compare two fractions without finding a common denominator. To use this method, you multiply the numerator of the first fraction by the denominator of the second fraction, and then multiply the numerator of the second fraction by the denominator of the first fraction. Then, you compare the two products. The fraction that corresponds to the larger product is the larger fraction.
For example, to compare 1/4 and 3/8 using cross-multiplication:
- Multiply 1 (numerator of the first fraction) by 8 (denominator of the second fraction): 1 * 8 = 8
- Multiply 3 (numerator of the second fraction) by 4 (denominator of the first fraction): 3 * 4 = 12
Since 12 is greater than 8, 3/8 is larger than 1/4.
Trends and Latest Developments
In modern mathematics education, a significant trend is emphasizing conceptual understanding over rote memorization. This means that instead of just teaching students the rules for comparing fractions, educators are focusing on helping them understand why these rules work. This approach enhances students' problem-solving skills and their ability to apply mathematical concepts in real-world scenarios.
There's also an increasing use of visual aids and technology in teaching fractions. Tools like fraction bars, pie charts, and interactive simulations help students visualize fractions and understand their relative sizes. These methods cater to different learning styles and make the abstract concept of fractions more concrete and accessible. Studies have shown that students who use visual aids have a better understanding of fractions and perform better on related tasks.
Data and Statistics
Recent studies on mathematics education have highlighted the importance of early intervention in fraction concepts. Research indicates that students who struggle with fractions in elementary school are more likely to face challenges in algebra and other advanced math courses. This has led to increased emphasis on teaching fractions effectively in the early grades.
Expert Opinions
Mathematics educators emphasize the significance of connecting fractions to real-life situations. By using examples that students can relate to, such as sharing pizzas or measuring ingredients in a recipe, teachers can make fractions more meaningful and engaging. Experts also recommend using a variety of methods to compare fractions, as different students may find different approaches more intuitive.
Tips and Expert Advice
Tip 1: Use Visual Aids
Visual aids can be incredibly helpful when comparing fractions, especially for those who are new to the concept.
- Fraction Bars: These are rectangular bars divided into equal parts, with each part representing a fraction. By comparing the lengths of the bars, you can easily see which fraction is larger.
- Pie Charts: These circular charts are divided into sectors, with each sector representing a fraction. Comparing the sizes of the sectors allows you to visualize the relative sizes of the fractions.
- Number Lines: Represent fractions as points on a number line. This can help you see the order and relative distance between different fractions.
Visual aids make fractions more concrete and less abstract. This can be particularly helpful for students who struggle with abstract concepts. Seeing the fractions visually can provide a more intuitive understanding of their relative sizes.
Tip 2: Simplify Fractions First
Simplifying fractions before comparing them can make the process much easier.
- Find the Greatest Common Factor (GCF): The GCF is the largest number that divides evenly into both the numerator and the denominator. Divide both the numerator and the denominator by the GCF to simplify the fraction.
- Example: If you are comparing 4/8 and 3/8, you can simplify 4/8 to 1/2 by dividing both the numerator and the denominator by 4. Now, comparing 1/2 and 3/8 is easier.
Simplifying fractions reduces the size of the numbers you are working with, which can make the comparison process less complicated. It also helps to reveal the underlying relationship between the fractions more clearly.
Tip 3: Convert to Decimals
Converting fractions to decimals is another effective way to compare them.
- Divide the Numerator by the Denominator: This will give you the decimal equivalent of the fraction.
- Example: To convert 1/4 to a decimal, divide 1 by 4, which equals 0.25. To convert 3/8 to a decimal, divide 3 by 8, which equals 0.375. Now, you can easily compare 0.25 and 0.375.
Decimals are easier to compare than fractions because they are based on the base-10 number system. Most people are more familiar with comparing decimals than fractions, making this method more intuitive for them.
Tip 4: Use Benchmarks
Benchmarks are common fractions that you can use as reference points when comparing other fractions.
- Common Benchmarks: 0, 1/4, 1/2, 3/4, and 1 are useful benchmarks.
- Example: If you are comparing 2/5 and 5/8, you can use 1/2 as a benchmark. 2/5 is less than 1/2, and 5/8 is greater than 1/2. Therefore, 5/8 is larger than 2/5.
Using benchmarks simplifies the comparison process by providing a familiar reference point. It allows you to quickly estimate the relative size of a fraction without having to perform complex calculations.
Tip 5: Practice Regularly
Like any skill, comparing fractions becomes easier with practice.
- Work through Examples: Solve a variety of fraction comparison problems to build your skills and confidence.
- Use Online Resources: There are many websites and apps that offer practice exercises and quizzes on fractions.
- Apply Fractions in Real-Life: Look for opportunities to use fractions in everyday situations, such as cooking, measuring, or sharing items with friends.
Regular practice reinforces your understanding of fractions and helps you develop fluency in comparing them. The more you work with fractions, the more comfortable and confident you will become.
FAQ
Q: What is a fraction? A: A fraction represents a part of a whole, written as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates how many parts of the whole you have, and the denominator indicates how many equal parts the whole is divided into.
Q: Why is it important to have a common denominator when comparing fractions? A: A common denominator allows you to compare fractions directly by looking at their numerators. When fractions have the same denominator, you are comparing parts of the same whole, making it easy to see which fraction represents a larger portion.
Q: What is cross-multiplication, and how does it work? A: Cross-multiplication is a method to compare two fractions without finding a common denominator. You multiply the numerator of the first fraction by the denominator of the second fraction, and then multiply the numerator of the second fraction by the denominator of the first fraction. By comparing the two products, you can determine which fraction is larger.
Q: How can visual aids help in comparing fractions? A: Visual aids like fraction bars, pie charts, and number lines make fractions more concrete and less abstract. They allow you to see the relative sizes of fractions, providing a more intuitive understanding.
Q: What are some common benchmarks for comparing fractions? A: Common benchmarks include 0, 1/4, 1/2, 3/4, and 1. These fractions can be used as reference points to quickly estimate the relative size of other fractions.
Conclusion
So, is 1/4 bigger than 3/8? No, it isn't. By converting 1/4 to 2/8, we can clearly see that 3/8 is larger. We explored several methods, including finding common denominators, cross-multiplication, and converting to decimals, to effectively compare fractions. Understanding these techniques not only enhances your mathematical skills but also equips you with practical tools for everyday problem-solving.
Now that you’ve gained a solid understanding of how to compare fractions, put your knowledge to the test! Try solving some practice problems or applying these concepts in real-life scenarios. Share your experiences and any additional tips you discover in the comments below. Let’s continue learning and growing together!
Latest Posts
Latest Posts
-
Choose All Of The Following That Are Ideologies
Nov 16, 2025
-
Chemical Formula For Carbon And Hydrogen
Nov 16, 2025
-
How To Find Perimeter Of Scalene Triangle
Nov 16, 2025
-
Who Were The Jacobins During The French Revolution
Nov 16, 2025
-
5 Letter Word With O U
Nov 16, 2025
Related Post
Thank you for visiting our website which covers about Is 1 4 Bigger Than 3 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.