Integral Of X 2 Ln X
catholicpriest
Nov 26, 2025 · 9 min read
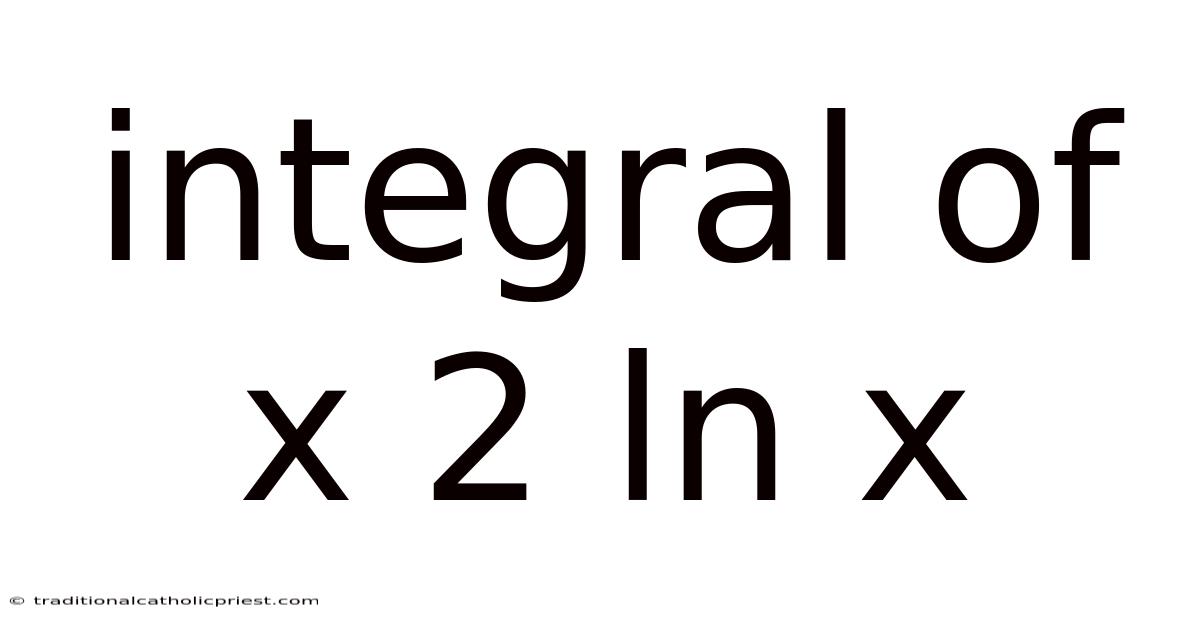
Table of Contents
Imagine you're baking a cake, and the recipe calls for a "pinch" of this and a "dash" of that. While approximations work sometimes, getting the perfect cake requires precise measurements. Similarly, in calculus, some integrals seem straightforward, while others require a bit more finesse. One such integral is the integral of x² ln x, which combines a polynomial term with a logarithmic one. It's not something you can solve with a simple power rule.
The integral of x² ln x embodies the beautiful dance between algebra and calculus. It's a problem that appears simple on the surface but demands a strategic approach. Successfully solving it is like cracking a code, revealing the underlying mathematical structure and solidifying our understanding of integration techniques. In this comprehensive guide, we’ll walk through the process step by step, exploring the essential concepts and practical tips needed to master this type of integral.
Main Subheading
When faced with the integral of x² ln x, the first question that arises is: how do we tackle it? The answer lies in a powerful technique called integration by parts. This method allows us to break down complex integrals into simpler, more manageable pieces. It's particularly useful when dealing with integrals that involve products of different types of functions, like polynomials and logarithms.
Integration by parts is not just a mathematical trick; it's a technique rooted in the product rule for differentiation. Understanding its foundation helps us appreciate its power and applicability. By carefully choosing which part of the integrand to differentiate and which to integrate, we can often transform a seemingly impossible integral into a solvable one. It's a bit like choosing the right tool for the job – with integration by parts, we're equipping ourselves with the perfect instrument to tackle the integral of x² ln x.
Comprehensive Overview
At its core, integration by parts is derived from the product rule of differentiation. The product rule states that for any two differentiable functions u(x) and v(x), the derivative of their product is given by:
d/dx [u(x)v(x)] = u'(x)v(x) + u(x)v'(x)
Integrating both sides with respect to x, we get:
∫ d/dx [u(x)v(x)] dx = ∫ u'(x)v(x) dx + ∫ u(x)v'(x) dx
This simplifies to:
u(x)v(x) = ∫ u'(x)v(x) dx + ∫ u(x)v'(x) dx
Rearranging the terms, we obtain the formula for integration by parts:
∫ u(x)v'(x) dx = u(x)v(x) - ∫ v(x)u'(x) dx
This formula tells us that the integral of a product u(x)v'(x) is equal to the product of u(x) and v(x), minus the integral of v(x)u'(x). The key to successfully using integration by parts lies in choosing u and v' wisely.
For the integral of x² ln x, we need to decide which function to assign as u and which as v'. A good rule of thumb is to choose u as the function that becomes simpler when differentiated, and v' as the function that is easy to integrate. In this case, ln x becomes simpler when differentiated, while x² is easy to integrate. Therefore, we let:
u = ln x v' = x²
Now we need to find u' and v:
u' = d/dx (ln x) = 1/x v = ∫ x² dx = (x³)/3
Applying the integration by parts formula, we have:
∫ x² ln x dx = (ln x)((x³)/3) - ∫ ((x³)/3)(1/x) dx
Simplifying the integral on the right:
∫ x² ln x dx = ((x³ ln x)/3) - (1/3) ∫ x² dx
Now, we can easily integrate x²:
∫ x² dx = (x³)/3 + C
So, the final result is:
∫ x² ln x dx = ((x³ ln x)/3) - (1/3)((x³)/3) + C
∫ x² ln x dx = ((x³ ln x)/3) - (x³)/9 + C
Where C is the constant of integration.
This constant is crucial because it represents the family of functions that have the same derivative. Omitting the constant of integration means we're only giving one specific antiderivative, rather than the general solution. The constant C accounts for the fact that the derivative of a constant is zero.
Trends and Latest Developments
While the technique of integration by parts has been a cornerstone of calculus for centuries, modern advancements in computational mathematics and software have streamlined the process of solving complex integrals. Tools like Wolfram Alpha, Mathematica, and Maple can handle integrals like ∫ x² ln x dx effortlessly, providing step-by-step solutions and graphical representations.
However, relying solely on these tools without understanding the underlying principles can be detrimental to one’s mathematical intuition and problem-solving skills. A recent trend in mathematics education emphasizes a balanced approach, where students learn both the manual techniques and the use of computational tools. This ensures that they can not only solve integrals but also understand the logic behind them, which is crucial for more advanced mathematical studies and applications.
Furthermore, there is growing interest in extending integration techniques to more complex functions and higher dimensions. For instance, researchers are exploring variations of integration by parts for multi-variable calculus and functional analysis. These developments are crucial for tackling problems in physics, engineering, and data science, where complex integrals often arise.
Professional insights suggest that mastering integration by parts remains a fundamental skill for anyone working in quantitative fields. While software can handle routine calculations, the ability to recognize when and how to apply integration by parts is invaluable for tackling novel problems and developing new mathematical models. It's a testament to the enduring relevance of classical techniques in the age of advanced technology.
Tips and Expert Advice
Successfully solving integrals using integration by parts involves more than just memorizing the formula. Here are some practical tips and expert advice to help you master this technique:
-
Choose u and v' Wisely: The most critical step is selecting the appropriate functions for u and v'. A helpful mnemonic is LIATE, which stands for Logarithmic, Inverse trigonometric, Algebraic, Trigonometric, Exponential. This acronym suggests the order in which you should choose u. For example, if you have a logarithmic function and an algebraic function, choose the logarithmic function as u. This approach often simplifies the integral. In the case of ∫ x² ln x dx, ln x is logarithmic and x² is algebraic, so choosing u = ln x is the correct approach.
-
Simplify After Each Step: After applying the integration by parts formula, simplify the resulting integral as much as possible before proceeding. This can involve algebraic manipulations, trigonometric identities, or other techniques. Simplifying the integral makes it easier to evaluate and reduces the likelihood of errors. For instance, in our example, after the first step, we simplified ∫ ((x³)/3)(1/x) dx to (1/3) ∫ x² dx, which is much easier to integrate.
-
Recognize When to Apply Integration by Parts Multiple Times: Some integrals require multiple applications of integration by parts. If the new integral you obtain after the first application is still complex, consider applying integration by parts again. This iterative process can eventually lead to a solvable integral. For example, consider the integral ∫ x² e**x dx. You would need to apply integration by parts twice to solve it.
-
Watch Out for Cyclic Integrals: In some cases, applying integration by parts leads to a cyclic integral, where the original integral reappears on the right side of the equation. In such cases, you can solve for the original integral algebraically. For example, consider ∫ e**x cos x dx. Applying integration by parts twice will lead you back to the original integral, allowing you to solve for it.
-
Practice Regularly: Like any mathematical skill, mastering integration by parts requires consistent practice. Work through a variety of examples, starting with simpler integrals and gradually progressing to more complex ones. The more you practice, the better you will become at recognizing when to use integration by parts and choosing the appropriate functions for u and v'. Also, don't hesitate to consult textbooks, online resources, and seek help from instructors or peers when you encounter difficulties.
FAQ
Q: What is integration by parts used for?
A: Integration by parts is a technique used to integrate the product of two functions. It's particularly useful when one function becomes simpler when differentiated, and the other is easy to integrate.
Q: How do I choose u and v' in integration by parts?
A: Use the LIATE rule as a guide: Logarithmic, Inverse trigonometric, Algebraic, Trigonometric, Exponential. Choose u in that order. The function that comes earlier in the list should be chosen as u.
Q: What if I need to apply integration by parts multiple times?
A: If the resulting integral after the first application is still complex, apply integration by parts again. Repeat as necessary until you obtain a solvable integral.
Q: What is a cyclic integral, and how do I solve it?
A: A cyclic integral is one where applying integration by parts leads back to the original integral. In such cases, solve for the original integral algebraically.
Q: Can I use software to solve integrals?
A: Yes, tools like Wolfram Alpha, Mathematica, and Maple can solve complex integrals. However, understanding the underlying principles is crucial for problem-solving and advanced mathematical studies.
Conclusion
In summary, solving the integral of x² ln x involves a methodical application of integration by parts. By carefully selecting u and v', and by simplifying the integral at each step, we can arrive at the solution: ((x³ ln x)/3) - (x³)/9 + C. This process not only demonstrates the power of integration by parts but also highlights the importance of understanding the underlying principles of calculus.
Now that you have a solid grasp of how to solve this type of integral, put your knowledge into practice. Try solving similar integrals and explore more complex problems. Don't be afraid to make mistakes – they are an essential part of the learning process. Share your solutions and insights with others, and continue to deepen your understanding of calculus. Your journey into the world of calculus has just begun, and there are countless more integrals to conquer.
Latest Posts
Latest Posts
-
How Many Pounds Is 1 5 Kg
Nov 27, 2025
-
Lateral Area Of Right Triangular Prism
Nov 27, 2025
-
How To Construct A Wind Vane
Nov 27, 2025
-
What Is The Difference Between Civil Law And Criminal Law
Nov 27, 2025
-
Describe Pasteurs Results And How They Helped Disprove Spontaneous Generation
Nov 27, 2025
Related Post
Thank you for visiting our website which covers about Integral Of X 2 Ln X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.