If The P Value Is Less Than 0.05
catholicpriest
Nov 19, 2025 · 12 min read
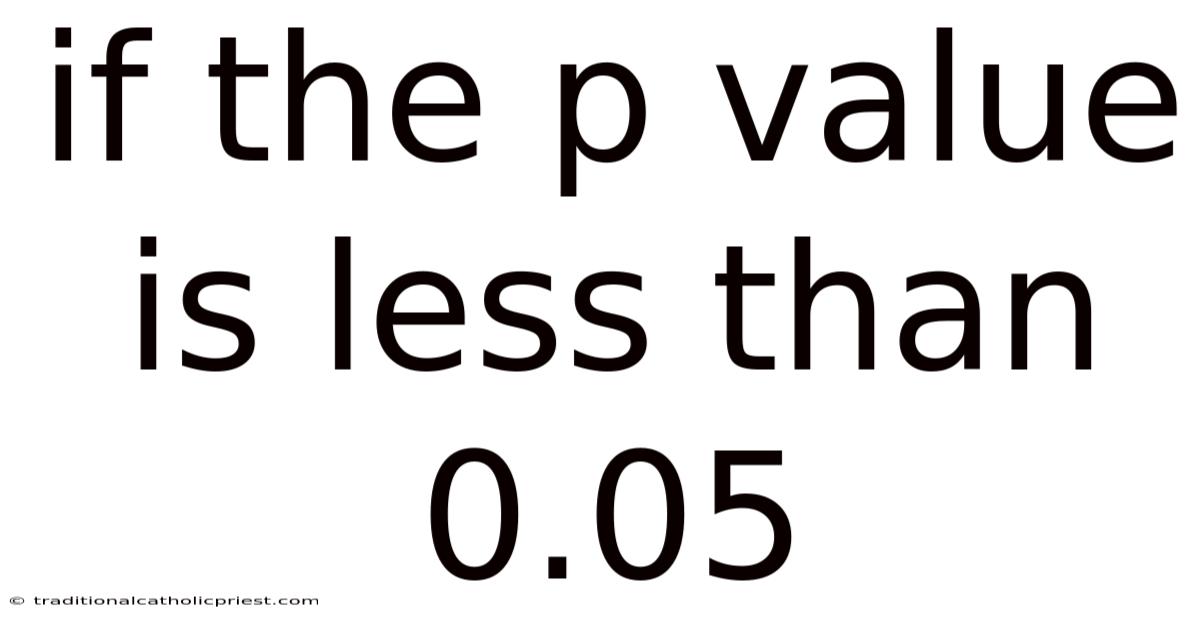
Table of Contents
Imagine you're a detective, piecing together clues at a crime scene. Each piece of evidence offers a glimpse into what might have happened. But how do you know which clues are genuine leads and which are merely red herrings? In the world of statistics, the p-value acts as your critical lens, helping you distinguish between real effects and random noise. A p-value less than 0.05 is often hailed as a significant finding, a breakthrough that warrants further investigation. But what does this seemingly simple threshold truly mean, and why has it become such a cornerstone of scientific research?
The journey of understanding a p-value below 0.05 begins with grasping its fundamental role in hypothesis testing. It's more than just a number; it’s a gateway to interpreting the validity of your research outcomes. Picture this: you’ve spent months conducting experiments, gathering data, and meticulously analyzing your results. Now, you’re faced with the burning question: are your findings meaningful, or are they just a fluke? The p-value steps in as your guide, offering a probabilistic assessment of the evidence against your initial assumption. This article will dive deep into the significance of a p-value less than 0.05, exploring its implications, limitations, and practical applications in the real world.
Main Subheading
At its core, the p-value is a statistical measure that quantifies the probability of observing results as extreme as, or more extreme than, the results obtained in a study, assuming that the null hypothesis is true. The null hypothesis is a statement of no effect or no difference. In simpler terms, it’s the assumption you're trying to disprove. For example, if you’re testing whether a new drug improves patient outcomes, the null hypothesis would be that the drug has no effect. The p-value then tells you how likely it is that you'd see the data you observed if the drug actually did nothing.
The convention of using 0.05 as a threshold for statistical significance originated from the work of Ronald Fisher, a prominent statistician in the early 20th century. Fisher suggested that a p-value of 0.05 could be used as a convenient cut-off for deciding whether to reject the null hypothesis. In his view, this threshold represented a reasonable balance between the risks of making false positive and false negative errors. A p-value less than 0.05 implies that there is a less than 5% chance of observing the obtained results if the null hypothesis were true. This is often interpreted as sufficient evidence to reject the null hypothesis and conclude that there is a statistically significant effect.
Comprehensive Overview
To truly understand the p-value, it’s essential to delve into its scientific foundations, historical context, and mathematical underpinnings. The concept of hypothesis testing and statistical significance is deeply rooted in probability theory and inferential statistics. Let’s begin by exploring the core concepts that make up the p-value.
-
Null Hypothesis: As mentioned earlier, the null hypothesis is a statement of no effect or no difference. It serves as the starting point for statistical testing. For instance, if you're comparing the average heights of two groups of people, the null hypothesis would be that there is no difference in their average heights.
-
Alternative Hypothesis: The alternative hypothesis is the statement that contradicts the null hypothesis. It proposes that there is a real effect or difference. In the height comparison example, the alternative hypothesis might be that the average height of one group is different from the average height of the other group.
-
Significance Level (Alpha): The significance level, denoted as α (alpha), is a pre-determined threshold used to decide whether to reject the null hypothesis. The most common significance level is 0.05, but other values such as 0.01 or 0.10 can also be used depending on the context and the level of certainty required. The significance level represents the maximum probability of making a Type I error (false positive).
-
Test Statistic: A test statistic is a numerical value calculated from the sample data that is used to evaluate the evidence against the null hypothesis. Examples of test statistics include the t-statistic, z-statistic, and chi-square statistic. The choice of the test statistic depends on the type of data and the specific hypothesis being tested.
-
P-value Calculation: The p-value is calculated based on the test statistic and the distribution of the test statistic under the null hypothesis. It represents the probability of observing a test statistic as extreme as, or more extreme than, the one calculated from the sample data, assuming that the null hypothesis is true. The p-value is used to assess the strength of the evidence against the null hypothesis.
The historical context of the p-value is closely tied to the development of statistical inference in the early 20th century. Ronald Fisher's contributions laid the groundwork for modern hypothesis testing and the use of p-values in scientific research. However, the widespread adoption of the 0.05 threshold has also been subject to criticism and debate. Some argue that it is an arbitrary cut-off that can lead to overemphasis on statistical significance at the expense of practical significance and other important considerations.
The mathematical foundations of the p-value involve probability theory and statistical distributions. The p-value is derived from the probability distribution of the test statistic under the null hypothesis. For example, if you are using a t-test to compare the means of two groups, the p-value would be calculated based on the t-distribution with the appropriate degrees of freedom. The exact mathematical formula for calculating the p-value depends on the specific test statistic and the distribution being used.
It's important to note that the p-value is not the probability that the null hypothesis is true. It is also not the probability that the alternative hypothesis is true. Instead, it is the probability of observing the data, or more extreme data, given that the null hypothesis is true. A small p-value suggests that the observed data are unlikely to have occurred by chance alone if the null hypothesis were true. This provides evidence against the null hypothesis, leading to its rejection.
Trends and Latest Developments
In recent years, there has been growing scrutiny of the use and interpretation of p-values in scientific research. The replication crisis, which refers to the difficulty in replicating the results of many published studies, has highlighted some of the limitations and potential misuses of p-values. This has led to discussions and proposals for alternative approaches to statistical inference.
One of the major trends is the emphasis on effect sizes and confidence intervals, in addition to p-values. Effect sizes provide a measure of the magnitude of the effect, while confidence intervals provide a range of plausible values for the true effect. Reporting effect sizes and confidence intervals can provide a more complete picture of the results and reduce the reliance on p-values alone.
Another trend is the increasing awareness of the potential for p-hacking, which involves manipulating data or analysis methods to obtain statistically significant results. P-hacking can lead to false positive findings and undermine the integrity of scientific research. Researchers are encouraged to preregister their study protocols and analysis plans to prevent p-hacking and increase the transparency of their research.
There is also a growing movement towards adopting Bayesian statistical methods, which provide a different framework for statistical inference. Bayesian methods allow researchers to incorporate prior knowledge or beliefs into their analysis and obtain probabilities about the hypotheses themselves, rather than just the probability of the data given the null hypothesis. Bayesian methods can be more intuitive and informative than traditional frequentist methods, but they also require more complex calculations and assumptions.
Professional insights suggest that a more nuanced approach to interpreting p-values is needed. Rather than blindly accepting or rejecting the null hypothesis based on a p-value threshold, researchers should consider the context of the study, the strength of the evidence, and the potential for bias or confounding factors. It is also important to consider the practical significance of the findings, not just the statistical significance.
Tips and Expert Advice
Understanding and applying p-values effectively requires a combination of statistical knowledge, critical thinking, and attention to detail. Here are some practical tips and expert advice to help you navigate the complexities of p-values and make informed decisions about your research.
-
Understand the Assumptions: Before conducting any statistical test, make sure you understand the assumptions underlying the test. Violating these assumptions can lead to inaccurate p-values and incorrect conclusions. For example, many statistical tests assume that the data are normally distributed. If your data are not normally distributed, you may need to use a non-parametric test or transform your data to meet the normality assumption.
-
Consider the Sample Size: The sample size of your study can have a significant impact on the p-value. With a small sample size, it may be difficult to detect a statistically significant effect, even if a real effect exists. Conversely, with a large sample size, even small and trivial effects may be statistically significant. It is important to choose an appropriate sample size that is large enough to detect meaningful effects but not so large that it leads to oversensitivity.
-
Control for Multiple Comparisons: When conducting multiple statistical tests, the probability of obtaining a statistically significant result by chance alone increases. This is known as the multiple comparisons problem. To address this issue, you may need to use a correction method, such as the Bonferroni correction or the false discovery rate (FDR) control, to adjust the p-values and reduce the risk of false positive findings.
-
Report Effect Sizes and Confidence Intervals: In addition to p-values, always report effect sizes and confidence intervals. Effect sizes provide a measure of the magnitude of the effect, while confidence intervals provide a range of plausible values for the true effect. This information can help you assess the practical significance of your findings and avoid over-reliance on p-values alone.
-
Interpret P-values in Context: Do not interpret p-values in isolation. Consider the context of your study, the strength of the evidence, and the potential for bias or confounding factors. A p-value less than 0.05 does not automatically mean that your findings are important or meaningful. It simply means that the observed data are unlikely to have occurred by chance alone if the null hypothesis were true.
-
Avoid P-hacking: Be aware of the potential for p-hacking and take steps to prevent it. Preregister your study protocols and analysis plans to increase the transparency of your research. Avoid making arbitrary changes to your data or analysis methods in order to obtain statistically significant results.
-
Seek Expert Advice: If you are unsure about how to interpret or apply p-values, seek advice from a statistician or experienced researcher. They can help you choose the appropriate statistical tests, interpret the results correctly, and avoid common pitfalls.
FAQ
Q: What does a p-value of 0.05 mean?
A: A p-value of 0.05 means that there is a 5% chance of observing results as extreme as, or more extreme than, the results obtained in your study, assuming that the null hypothesis is true.
Q: Is a p-value of 0.06 significant?
A: Traditionally, a p-value of 0.06 is not considered statistically significant because it is above the conventional threshold of 0.05. However, some researchers may consider it marginally significant and worthy of further investigation, especially if the study has other strengths or the effect size is large.
Q: Can a p-value tell me the probability that my hypothesis is true?
A: No, a p-value does not tell you the probability that your hypothesis is true. It only tells you the probability of observing the data, or more extreme data, given that the null hypothesis is true.
Q: What is the difference between statistical significance and practical significance?
A: Statistical significance refers to the probability of observing the data, or more extreme data, given that the null hypothesis is true. Practical significance refers to the real-world importance or relevance of the findings. A result can be statistically significant but not practically significant, and vice versa.
Q: How can I reduce the risk of false positive findings?
A: You can reduce the risk of false positive findings by using a more stringent significance level (e.g., 0.01 instead of 0.05), controlling for multiple comparisons, reporting effect sizes and confidence intervals, and avoiding p-hacking.
Conclusion
In conclusion, the p-value is a critical tool in statistical hypothesis testing, providing a measure of the evidence against the null hypothesis. A p-value less than 0.05 is often interpreted as statistically significant, indicating that the observed data are unlikely to have occurred by chance alone if the null hypothesis were true. However, it's crucial to understand the limitations of p-values and interpret them in context, considering factors such as effect sizes, confidence intervals, and the potential for bias.
To enhance your research and statistical analysis skills, consider exploring advanced statistical techniques, engaging in collaborative research, and staying updated with the latest developments in statistical methodology. By adopting a comprehensive and critical approach to p-values, you can make more informed decisions and contribute to the advancement of knowledge in your field. What are your thoughts on the use of p-values in research? Share your experiences and insights in the comments below, and let's foster a community of informed and critical thinkers!
Latest Posts
Latest Posts
-
What Is Bigger Megabyte Or Kilobyte
Nov 19, 2025
-
What Is The Worlds Largest Saltwater Lake
Nov 19, 2025
-
Whats The Difference Between A Job And A Career
Nov 19, 2025
-
Can You Keep A Panther As A Pet
Nov 19, 2025
-
Show The Tens Fact You Used Write The Difference
Nov 19, 2025
Related Post
Thank you for visiting our website which covers about If The P Value Is Less Than 0.05 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.