Cos X/1-sin X + Cos X/1+sin X
catholicpriest
Nov 10, 2025 · 8 min read
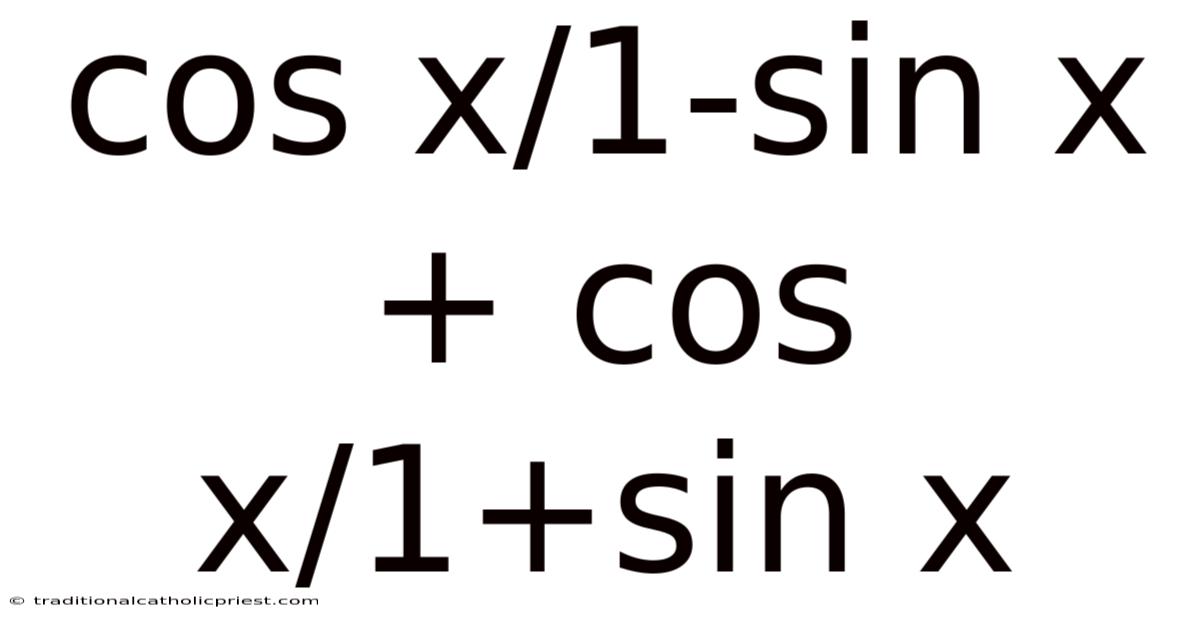
Table of Contents
The rhythmic crashing of waves, the gentle sway of trees in the wind, the consistent beat of our hearts—all these phenomena can be modeled with the help of trigonometric functions. Among these, the dance between sine and cosine, expressed in equations, unlocks a deeper understanding of cyclical events. Have you ever wondered how seemingly simple trigonometric expressions can reveal intricate relationships?
Consider the expression cos x/(1-sin x) + cos x/(1+sin x). At first glance, it might seem like just another mathematical problem. However, by manipulating it using trigonometric identities and algebraic techniques, we can simplify it into a more elegant form. This simplification not only makes the expression easier to work with but also provides insight into the fundamental connections between sine and cosine. Let's delve into the process of simplifying this expression, uncovering the underlying principles and practical applications along the way.
Main Subheading
The expression cos x/(1-sin x) + cos x/(1+sin x) is a trigonometric equation that can be simplified using algebraic manipulations and trigonometric identities. Simplifying trigonometric expressions is a fundamental skill in mathematics, particularly in calculus, physics, and engineering. These simplifications often reveal underlying relationships and make complex problems more manageable.
In many scientific and engineering applications, trigonometric functions are used to model cyclical phenomena. Simplifying these functions can lead to more efficient computations and a better understanding of the system being modeled. For instance, in signal processing, simplifying trigonometric expressions can help in analyzing and filtering signals more effectively. Similarly, in physics, these simplifications can aid in understanding wave behavior and oscillations.
Comprehensive Overview
To simplify the given expression, we will employ algebraic techniques and trigonometric identities. Here's a step-by-step breakdown:
- Combine the Fractions: The first step is to combine the two fractions into a single fraction. To do this, we find a common denominator.
- Simplify the Numerator: After combining the fractions, we simplify the numerator by applying trigonometric identities.
- Apply Trigonometric Identities: We use the Pythagorean identity sin^2 x + cos^2 x = 1 to further simplify the expression.
- Further Simplification: We look for opportunities to cancel out terms or further simplify the expression to arrive at the simplest form.
Now, let's execute these steps in detail. The expression is:
cos x/(1-sin x) + cos x/(1+sin x)
To combine the fractions, we find the common denominator, which is (1 - sin x)(1 + sin x). Thus, we rewrite the expression as:
[cos x(1 + sin x) + cos x(1 - sin x)] / [(1 - sin x)(1 + sin x)]
Next, we expand the numerator:
(cos x + cos x sin x + cos x - cos x sin x) / [(1 - sin x)(1 + sin x)]
Notice that cos x sin x and -cos x sin x cancel each other out:
(2 cos x) / [(1 - sin x)(1 + sin x)]
Now, let’s simplify the denominator. Using the difference of squares formula, (a - b)(a + b) = a^2 - b^2, we get:
1 - sin^2 x
We know from the Pythagorean trigonometric identity that sin^2 x + cos^2 x = 1. Therefore, 1 - sin^2 x = cos^2 x. Substituting this into our expression, we have:
(2 cos x) / (cos^2 x)
Finally, we can cancel out a factor of cos x from the numerator and the denominator:
2 / cos x
The reciprocal of cosine is secant, so we can write this as:
2 sec x
Thus, the simplified form of the expression cos x/(1-sin x) + cos x/(1+sin x) is 2 sec x. This simplification illustrates how algebraic manipulation, combined with trigonometric identities, can reduce a seemingly complex expression to a much simpler form.
The simplification process not only reduces the complexity of the expression but also provides a different perspective on the relationship between sine and cosine. In many applications, simpler forms are easier to analyze and compute.
Trends and Latest Developments
In recent years, the use of trigonometric functions has expanded beyond traditional fields like physics and engineering to include areas like computer graphics, data analysis, and machine learning. Researchers are constantly developing new algorithms and techniques to efficiently compute and manipulate trigonometric expressions.
One notable trend is the increasing use of symbolic computation software like Mathematica, Maple, and SageMath. These tools can automatically simplify complex trigonometric expressions, making them invaluable for researchers and engineers. Additionally, advances in numerical methods have led to more accurate and efficient ways of evaluating trigonometric functions in computational models.
Another area of development is the application of trigonometric functions in machine learning, particularly in models dealing with time series data and cyclical patterns. Techniques like Fourier analysis, which rely heavily on trigonometric functions, are being used to extract meaningful features from complex datasets.
From a professional standpoint, understanding how to simplify trigonometric expressions remains a crucial skill for anyone working in STEM fields. The ability to manipulate these expressions can lead to more efficient problem-solving and a deeper understanding of the underlying principles.
Tips and Expert Advice
Simplifying trigonometric expressions can be challenging, but with the right strategies, it becomes more manageable. Here are some practical tips and expert advice to help you master this skill:
- Master Fundamental Identities: The foundation of simplifying trigonometric expressions lies in a solid understanding of basic trigonometric identities.
- Look for Common Denominators: When dealing with fractions, finding a common denominator is often the first step.
- Recognize Pythagorean Identities: The Pythagorean identities (sin^2 x + cos^2 x = 1, tan^2 x + 1 = sec^2 x, and cot^2 x + 1 = csc^2 x) are essential tools for simplifying expressions.
- Use Algebraic Techniques: Don't forget to apply basic algebraic techniques like factoring, expanding, and canceling terms.
- Practice Regularly: Like any mathematical skill, practice is key. Work through a variety of problems to build your confidence and intuition.
Let's delve deeper into each of these tips to provide more practical advice and real-world examples.
Master Fundamental Identities: Knowing the fundamental trigonometric identities is crucial. These include reciprocal identities (e.g., sec x = 1/cos x), quotient identities (e.g., tan x = sin x/cos x), and Pythagorean identities. For example, if you see sec^2 x - 1 in an expression, immediately recognize that it can be simplified to tan^2 x using the identity tan^2 x + 1 = sec^2 x.
Look for Common Denominators: When adding or subtracting fractions involving trigonometric functions, finding a common denominator is usually the first step. For instance, if you have (1/sin x) + (1/cos x), the common denominator is sin x cos x, and the expression becomes (cos x + sin x) / (sin x cos x).
Recognize Pythagorean Identities: The Pythagorean identities are powerful tools for simplification. Whenever you see sin^2 x + cos^2 x, replace it with 1. Similarly, look for opportunities to use tan^2 x + 1 = sec^2 x and cot^2 x + 1 = csc^2 x. For example, if you have an expression like 1 - cos^2 x, recognize that it simplifies to sin^2 x.
Use Algebraic Techniques: Algebraic techniques like factoring, expanding, and canceling terms are just as important as trigonometric identities. For example, if you have an expression like sin^2 x - cos^2 x, recognize that it can be factored as (sin x + cos x)(sin x - cos x).
Practice Regularly: The more you practice, the better you'll become at recognizing patterns and applying the appropriate techniques. Work through a variety of problems, starting with simpler ones and gradually moving to more complex ones.
FAQ
Q: Why is it important to simplify trigonometric expressions?
A: Simplifying trigonometric expressions makes them easier to work with, reduces computational complexity, and often reveals underlying relationships.
Q: What are the basic trigonometric identities I should know?
A: Key identities include reciprocal identities (sec x = 1/cos x, csc x = 1/sin x, cot x = 1/tan x), quotient identities (tan x = sin x/cos x, cot x = cos x/sin x), and Pythagorean identities (sin^2 x + cos^2 x = 1, tan^2 x + 1 = sec^2 x, cot^2 x + 1 = csc^2 x).
Q: How do I find a common denominator when adding or subtracting trigonometric fractions?
A: Identify the denominators of the fractions, and find the least common multiple (LCM). Multiply each fraction by a form of 1 that will give it the common denominator.
Q: What algebraic techniques are useful for simplifying trigonometric expressions?
A: Factoring, expanding, combining like terms, and using the difference of squares formula are all helpful algebraic techniques.
Q: Can symbolic computation software help with simplifying trigonometric expressions?
A: Yes, tools like Mathematica, Maple, and SageMath can automatically simplify complex trigonometric expressions.
Conclusion
In summary, simplifying the expression cos x/(1-sin x) + cos x/(1+sin x) to 2 sec x involves combining fractions, applying trigonometric identities, and using algebraic manipulation. This process underscores the interconnectedness of trigonometric functions and the power of simplification in revealing fundamental relationships. Understanding these principles is crucial for anyone working with mathematical models in science, engineering, or related fields.
Now that you've explored this simplification, why not try applying these techniques to other trigonometric expressions? Share your experiences and any further questions in the comments below. Let's continue the conversation and deepen our understanding of trigonometric functions together.
Latest Posts
Latest Posts
-
What Does Personification Mean In Poetry
Nov 10, 2025
-
Can You Square A Negative Number
Nov 10, 2025
-
How Do You Write 0 83 As A Fraction
Nov 10, 2025
-
5 Letter Words With B At The End
Nov 10, 2025
-
1 2 Teaspoon Baking Powder To Baking Soda
Nov 10, 2025
Related Post
Thank you for visiting our website which covers about Cos X/1-sin X + Cos X/1+sin X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.