5 8 Bigger Than 3 4
catholicpriest
Nov 21, 2025 · 12 min read
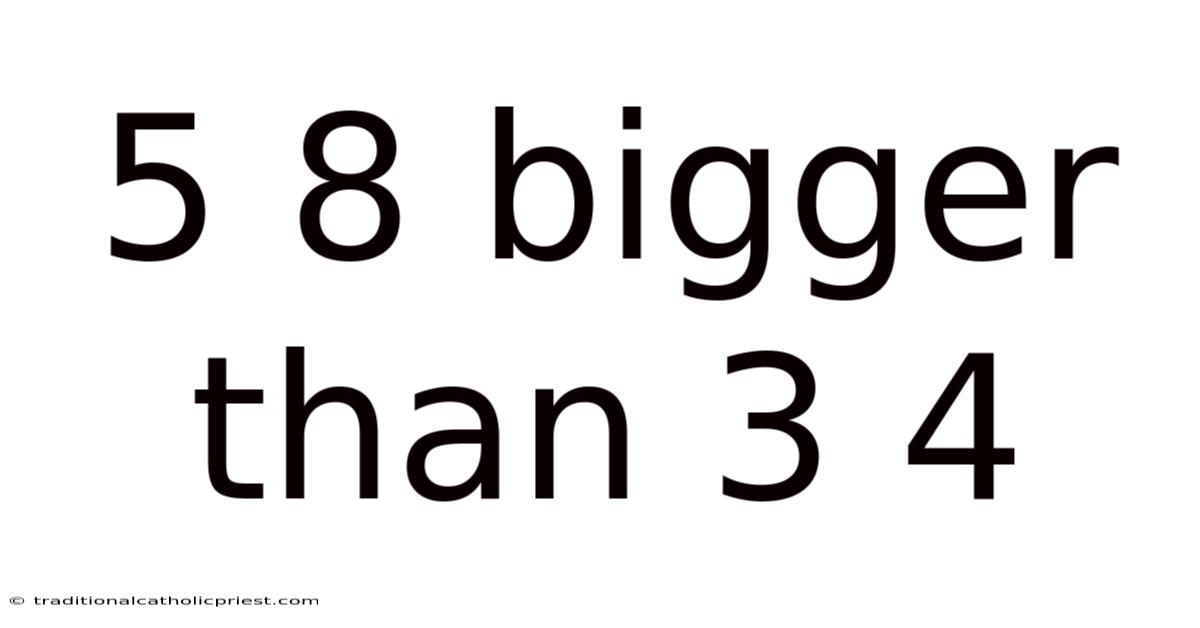
Table of Contents
Imagine you're baking a pizza and have two hungry friends coming over. You have two options: cut the pizza into four slices and give them three, or cut it into eight slices and give them five. Which option gives your friends a bigger share? This simple scenario introduces a fundamental concept in mathematics: comparing fractions. Understanding which fraction is bigger than another is not just a mathematical exercise; it's a skill we use daily, from splitting a bill to understanding proportions in recipes.
The ability to compare fractions, like determining whether 5/8 is bigger than 3/4, is a critical mathematical skill that extends far beyond the classroom. It empowers us to make informed decisions, understand proportions, and solve practical problems. This skill forms the bedrock of more advanced mathematical concepts, such as algebra and calculus, and is essential in various fields, including science, engineering, finance, and even the arts. Whether you're a student tackling homework, a professional analyzing data, or simply someone trying to make the best choice in everyday situations, a solid grasp of fraction comparison is indispensable. Let's explore the intricacies of comparing 5/8 and 3/4, and discover methods that make this comparison clear and understandable.
Main Subheading
At first glance, comparing fractions like 5/8 and 3/4 might seem confusing. Fractions represent parts of a whole, and the way those parts are divided can make direct comparison tricky. The denominator (the bottom number) tells us how many equal parts the whole is divided into, while the numerator (the top number) tells us how many of those parts we have. In the case of 5/8, the whole is divided into eight parts, and we have five of them. For 3/4, the whole is divided into four parts, and we have three of them. To effectively compare these fractions, we need a consistent basis for comparison.
To truly understand whether 5/8 is bigger than 3/4, we need to delve into the underlying principles of fractions and comparison. Fractions are essentially a way to represent a part of a whole, expressing a quantity relative to that whole. The key to comparing fractions lies in ensuring they refer to the same whole and are divided into the same number of parts. By finding a common denominator, we create a level playing field that allows us to directly compare the numerators and determine which fraction represents a larger portion. This process not only simplifies the comparison but also provides a deeper understanding of the proportional relationships between different fractions.
Comprehensive Overview
Definition of Fractions
A fraction represents a part of a whole. It consists of two numbers: the numerator and the denominator. The numerator indicates how many parts of the whole we have, while the denominator indicates the total number of equal parts into which the whole is divided. For example, in the fraction 5/8, '5' is the numerator, and '8' is the denominator. This means we have 5 parts out of a total of 8 equal parts. Understanding this basic structure is crucial for any operation involving fractions, including comparison.
The Importance of a Common Denominator
The cornerstone of comparing fractions lies in the concept of a common denominator. To accurately determine which fraction is larger, both fractions must have the same denominator. This ensures that the "wholes" being compared are divided into the same number of equal parts. Once fractions share a common denominator, comparing them becomes as simple as comparing their numerators: the fraction with the larger numerator is the larger fraction. Finding the least common multiple (LCM) of the denominators is often the most efficient way to find a common denominator, as it results in smaller numbers and simplifies calculations.
Methods for Finding a Common Denominator
Several methods can be used to find a common denominator. One common approach is to list the multiples of each denominator until a common multiple is found. For example, to compare 5/8 and 3/4, we can list the multiples of 8 (8, 16, 24, ...) and 4 (4, 8, 12, ...). The least common multiple is 8, making it the ideal common denominator. Another method involves multiplying the denominators together, although this may not always yield the least common denominator. Regardless of the method, the goal is to find a denominator that both original denominators can divide into evenly.
Converting Fractions to Equivalent Forms
Once a common denominator is identified, the next step is to convert each fraction into an equivalent fraction with the new denominator. An equivalent fraction represents the same value as the original fraction but has a different numerator and denominator. To convert a fraction, multiply both the numerator and the denominator by the same number. For instance, to convert 3/4 to an equivalent fraction with a denominator of 8, we multiply both the numerator and the denominator by 2 (3 x 2 = 6, 4 x 2 = 8), resulting in the equivalent fraction 6/8. This process ensures that the value of the fraction remains unchanged while allowing for direct comparison.
Comparing Fractions with the Same Denominator
With both fractions now having the same denominator, the comparison is straightforward. Simply compare the numerators: the fraction with the larger numerator is the larger fraction. In our example, we are comparing 5/8 and 6/8 (the equivalent of 3/4). Since 6 is greater than 5, 6/8 is greater than 5/8. Therefore, 3/4 is greater than 5/8. This direct comparison is the ultimate goal of finding a common denominator, providing a clear and unambiguous way to determine the relative size of two or more fractions.
Trends and Latest Developments
The landscape of mathematics education is constantly evolving, with educators continually seeking innovative methods to enhance students' comprehension of fractions and related concepts. A significant trend involves the integration of visual aids and manipulatives, such as fraction bars, pie charts, and interactive software, to provide students with a tangible and intuitive understanding of fractional relationships. These tools help bridge the gap between abstract mathematical concepts and concrete representations, making it easier for students to visualize and compare fractions.
Another notable trend is the emphasis on real-world applications of fractions. Instead of merely memorizing rules and procedures, students are encouraged to explore how fractions are used in everyday contexts, such as cooking, measuring, and financial planning. By connecting fractions to practical scenarios, educators can increase student engagement and motivation, fostering a deeper appreciation for the relevance and utility of mathematical concepts. Furthermore, the rise of personalized learning and adaptive technologies has enabled educators to tailor instruction to meet the individual needs of students, providing targeted support and enrichment opportunities to ensure mastery of fractions and other essential mathematical skills.
From a professional perspective, modern data analysis and statistical software heavily rely on fractional and proportional reasoning. Professionals in fields like finance, engineering, and science use these tools to model complex systems, analyze data sets, and make informed decisions. The ability to accurately compare and manipulate fractions is crucial for interpreting results and drawing meaningful conclusions. Moreover, the increasing emphasis on data visualization has led to the development of sophisticated techniques for representing fractional data in a clear and intuitive manner. This includes the use of interactive dashboards, charts, and graphs that allow users to explore and compare fractional relationships with ease.
Tips and Expert Advice
Use Visual Aids
One of the most effective ways to understand and compare fractions is by using visual aids. Drawing diagrams, such as circles or rectangles, and dividing them into equal parts can help visualize the fractions. For example, draw two identical rectangles. Divide one into eight equal parts and shade five of them to represent 5/8. Divide the other into four equal parts and shade three of them to represent 3/4. By visually comparing the shaded areas, you can easily see which fraction represents a larger portion. This method is particularly useful for students and anyone who struggles with abstract mathematical concepts.
Visual aids not only simplify the comparison process but also reinforce the fundamental concept of fractions as parts of a whole. They provide a concrete representation that can be easily understood and remembered, making it easier to grasp the underlying principles of fractional relationships. Additionally, visual aids can be used to demonstrate equivalent fractions, showing how different fractions can represent the same portion of a whole. This hands-on approach is invaluable for building a strong foundation in fractions and promoting a deeper understanding of mathematical concepts.
Cross-Multiplication Method
Another efficient technique for comparing two fractions is cross-multiplication. To compare fractions a/b and c/d, multiply a by d and b by c. Then, compare the two products. If a x d is greater than b x c, then a/b is greater than c/d. If a x d is less than b x c, then a/b is less than c/d. If a x d is equal to b x c, then the fractions are equal. For our example, 5/8 and 3/4, we multiply 5 x 4 = 20 and 8 x 3 = 24. Since 20 is less than 24, 5/8 is less than 3/4. This method is quick and doesn't require finding a common denominator, making it useful for quick comparisons.
The cross-multiplication method is a powerful shortcut that can be applied to any pair of fractions, regardless of their denominators. It is based on the principle of multiplying both fractions by the same common denominator, effectively eliminating the denominators and allowing for a direct comparison of the numerators. This technique is particularly useful when dealing with fractions that have large or complex denominators, as it avoids the need to find the least common multiple. However, it is important to remember that cross-multiplication only works for comparing two fractions at a time and cannot be directly applied to comparing multiple fractions simultaneously.
Convert to Decimals
Converting fractions to decimals provides another easy way to compare them. Divide the numerator by the denominator to get the decimal equivalent of the fraction. For example, 5/8 is equal to 0.625, and 3/4 is equal to 0.75. Comparing the decimal values, we see that 0.75 is greater than 0.625, so 3/4 is greater than 5/8. This method is particularly useful when you are comfortable with decimal operations or have access to a calculator.
Converting fractions to decimals simplifies the comparison process by expressing both fractions in a common numerical format. Decimals are easier to compare than fractions, especially when dealing with fractions that have different denominators. This method is also useful for comparing fractions with other numbers, such as whole numbers or percentages. However, it is important to remember that some fractions may result in repeating decimals, which may require rounding to a certain number of decimal places for accurate comparison.
Simplify Fractions First
Before comparing fractions, always check if they can be simplified. Simplifying fractions involves dividing both the numerator and the denominator by their greatest common factor (GCF). For instance, if you were comparing 4/8 and 3/4, you could simplify 4/8 to 1/2 by dividing both the numerator and the denominator by 4. Now you can easily compare 1/2 and 3/4. This step can make the comparison process much easier, especially when dealing with large numbers.
Simplifying fractions reduces them to their simplest form, making it easier to identify equivalent fractions and compare their values. This process also helps to avoid unnecessary complications when performing mathematical operations with fractions. Simplifying fractions is a fundamental skill that should be mastered before attempting more complex operations, as it lays the groundwork for a deeper understanding of fractional relationships. Furthermore, simplifying fractions can reveal hidden patterns and relationships, making it easier to solve problems and make informed decisions.
Practice Regularly
Like any skill, mastering the comparison of fractions requires practice. Work through various examples, starting with simple fractions and gradually moving to more complex ones. Use different methods to compare the same fractions to reinforce your understanding. The more you practice, the more comfortable and confident you will become in comparing fractions.
Regular practice is the key to developing fluency and proficiency in any mathematical skill, including the comparison of fractions. By consistently working through a variety of examples, you will reinforce your understanding of the underlying concepts and develop the ability to quickly and accurately compare fractions. Practice also helps to identify areas where you may be struggling, allowing you to seek additional support and clarification. Furthermore, regular practice builds confidence and reduces anxiety when faced with mathematical problems, making it easier to approach challenges with a positive and proactive mindset.
FAQ
Q: Why is it important to find a common denominator when comparing fractions? A: Finding a common denominator ensures that you're comparing fractions that represent parts of the same whole, divided into the same number of equal pieces. This allows for an accurate comparison of the numerators.
Q: What is cross-multiplication, and how does it help in comparing fractions? A: Cross-multiplication is a shortcut method where you multiply the numerator of one fraction by the denominator of the other and vice versa. Comparing the resulting products tells you which fraction is larger without needing a common denominator.
Q: Can I always convert fractions to decimals to compare them? A: Yes, converting fractions to decimals is a valid method for comparison. However, be aware that some fractions result in repeating decimals, which may require rounding for practical comparison.
Q: What should I do if the fractions have very large denominators? A: If the denominators are large, try to simplify the fractions first. If simplification doesn't help, cross-multiplication might be a quicker method than finding a common denominator.
Q: How does understanding fractions help in real life? A: Understanding fractions is crucial in many real-life situations, such as cooking, measuring, managing finances, understanding proportions in various fields, and making informed decisions in everyday scenarios.
Conclusion
In summary, determining whether 5/8 is bigger than 3/4 involves understanding the fundamental principles of fractions and employing effective comparison techniques. By finding a common denominator, converting to decimals, or using cross-multiplication, you can accurately compare fractions and apply this knowledge to various practical situations. Mastering this skill enhances your mathematical proficiency and empowers you to make informed decisions in everyday life.
Ready to put your fraction comparison skills to the test? Try comparing different sets of fractions using the methods discussed. Share your findings or ask any further questions in the comments below!
Latest Posts
Latest Posts
-
How Many Color In The World
Nov 21, 2025
-
What Part Of Bacteria Helps It Move
Nov 21, 2025
-
Condensed Structural Formula For Carboxylic Acid
Nov 21, 2025
-
Is Sin 1 The Same As Arcsin
Nov 21, 2025
-
How To Find Area Of Shaded Region Of A Circle
Nov 21, 2025
Related Post
Thank you for visiting our website which covers about 5 8 Bigger Than 3 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.