4/3 Divided By 2 In Fraction
catholicpriest
Nov 08, 2025 · 11 min read
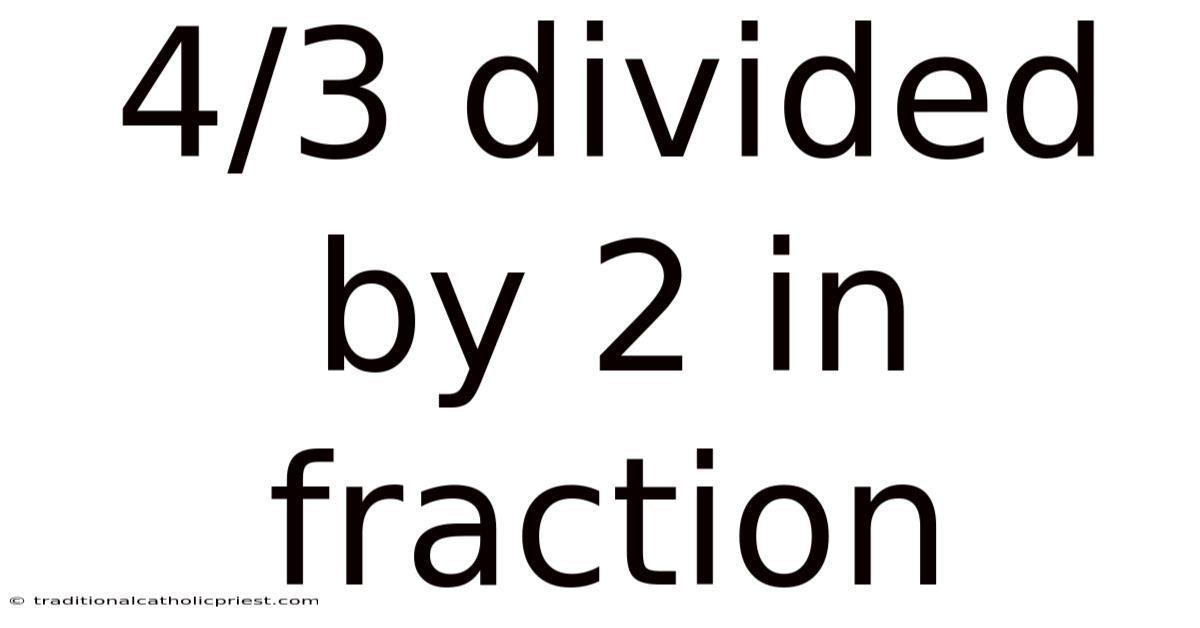
Table of Contents
Imagine you're baking a cake for a friend's birthday, and the recipe calls for 4/3 cups of flour. But, uh oh! You realize this recipe is actually for two cakes. How much flour do you need for just one cake? That’s where dividing fractions comes in handy. At first glance, dividing 4/3 by 2 might seem a bit tricky. Do you divide both the top and bottom numbers? Do you need some kind of magical fraction-busting tool? Fear not! It's much simpler than you think.
The secret lies in understanding what division really means when we're dealing with fractions. We're not just blindly crunching numbers; we're figuring out how to split something into equal parts. In this case, we want to take our 4/3 cups of flour and divide it evenly into two portions. Let's explore the world of fraction division together and uncover the secrets to solving problems like this with ease.
Diving into Fraction Division: 4/3 Divided by 2
Fraction division, at its core, involves figuring out how many times one fraction fits into another, or, as in our example, how to split a fraction into equal parts. Understanding this concept is crucial in various fields, from cooking and baking to engineering and finance. The seemingly simple problem of dividing 4/3 by 2 unveils the fundamental principles of fraction manipulation.
Defining Fractions and Division
Before we dive into the mechanics, let's quickly refresh our understanding of fractions. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). For example, in the fraction 4/3, 4 is the numerator, representing the number of parts we have, and 3 is the denominator, representing the total number of parts that make up the whole.
Division, in its simplest form, is the process of splitting a quantity into equal groups or determining how many times one quantity is contained within another. When dividing fractions, we are essentially asking how many times one fraction "goes into" another. However, instead of directly dividing, we employ a clever trick: multiplying by the reciprocal.
The Reciprocal: Flipping the Script
The reciprocal of a fraction is simply that fraction flipped upside down. The numerator becomes the denominator, and the denominator becomes the numerator. For instance, the reciprocal of 2 (which can be written as the fraction 2/1) is 1/2. The reciprocal of 3/4 is 4/3.
Why is the reciprocal so important? Because dividing by a number is the same as multiplying by its reciprocal! This is the key to simplifying fraction division.
The Mechanics: Dividing 4/3 by 2
Now, let's apply this knowledge to our problem: 4/3 divided by 2.
-
Rewrite the whole number as a fraction: Any whole number can be written as a fraction by placing it over 1. So, 2 becomes 2/1.
-
Find the reciprocal of the divisor: The divisor is the number we are dividing by (in this case, 2/1). The reciprocal of 2/1 is 1/2.
-
Multiply by the reciprocal: Instead of dividing 4/3 by 2/1, we multiply 4/3 by 1/2. (4/3) * (1/2) = (4 * 1) / (3 * 2) = 4/6
-
Simplify the result: The fraction 4/6 can be simplified by dividing both the numerator and the denominator by their greatest common factor, which is 2. 4/6 = (4 ÷ 2) / (6 ÷ 2) = 2/3
Therefore, 4/3 divided by 2 equals 2/3. This means that if you have 4/3 cups of flour and want to divide it equally into two portions, each portion will contain 2/3 cups of flour.
Visualizing Fraction Division
It can be helpful to visualize fraction division to solidify understanding. Imagine a pie that is divided into three equal slices. You have four of these slices, representing 4/3 of a pie (one whole pie and one extra slice). Now, you want to divide this amount equally between two people.
Each person would receive one full slice (1/3) and half of another slice (1/6). Together, this equals 1/3 + 1/6 = 2/6 + 1/6 = 3/6 = 1/2 of the original pie slices. Since we started with four slices, and ended up with two portions of pie slice, this doesn't quite represent our problem.
Let's think of it this way instead. Imagine a rectangle divided into three equal vertical sections. Shade in all three, representing 3/3, or one whole rectangle. Now shade in another vertical third, so you have 4/3 total shaded. You want to divide that shaded area into two equal parts.
If you draw a horizontal line right through the middle of the whole area that is shaded, you will see that half of the shaded area is equal to two of those smaller rectangle parts (1/3 each). So dividing 4/3 by 2 will yield 2/3 as our answer.
The Importance of Understanding "Of"
The word "of" often implies multiplication in mathematics, and it's crucial to distinguish it from division in certain contexts. For example, "1/2 of 4/3" means (1/2) * (4/3) = 2/3. This is the same result as dividing 4/3 by 2, but the meaning and the process leading to the solution are slightly different. Understanding the context in which the word "of" is used is key to avoiding confusion.
In essence, dividing 4/3 by 2 means finding one-half of 4/3. While the calculation is the same, recognizing the subtle difference in wording can aid in problem-solving and comprehension.
Trends and Latest Developments in Fraction Education
Fraction education has evolved significantly in recent years, influenced by both pedagogical research and technological advancements. There's a growing emphasis on conceptual understanding rather than rote memorization of rules.
The Rise of Visual and Interactive Learning
Educators are increasingly employing visual aids, such as fraction bars, number lines, and interactive simulations, to help students grasp the fundamental concepts of fractions. These tools provide a tangible representation of fractions, making them easier to understand and manipulate. Interactive simulations, in particular, allow students to experiment with different fraction operations and visualize the results in real-time. This hands-on approach fosters a deeper understanding of fraction concepts and improves retention.
Integrating Technology in the Classroom
Technology is playing an increasingly important role in fraction education. Educational apps, online games, and interactive websites offer engaging ways for students to practice and reinforce their fraction skills. These resources often provide personalized feedback, allowing students to identify and address their weaknesses. Adaptive learning platforms can tailor the difficulty level to each student's individual needs, ensuring that they are challenged appropriately.
Focus on Real-World Applications
Another trend in fraction education is the emphasis on real-world applications. Educators are striving to connect fraction concepts to everyday situations, such as cooking, baking, and measuring. By demonstrating the relevance of fractions in real-life contexts, they can motivate students to learn and appreciate the value of these mathematical concepts. For example, students might be asked to calculate the amount of ingredients needed to double a recipe or to determine the fraction of a pizza that each person will receive.
Addressing Common Misconceptions
Research has identified several common misconceptions that students often have about fractions. These misconceptions include the belief that the larger the denominator, the larger the fraction, or that fractions can only be added or subtracted if they have the same numerator. Educators are now more aware of these common pitfalls and are actively addressing them through targeted instruction and interventions.
Professional Insights
From a professional standpoint, educators are continually refining their teaching strategies to improve student outcomes in fraction education. This includes ongoing professional development, collaboration among teachers, and the use of data to inform instructional decisions. By staying abreast of the latest research and best practices, educators can ensure that they are providing students with the most effective and engaging fraction instruction possible. Furthermore, a collaborative approach involving parents and the community can create a supportive learning environment that fosters student success in mathematics.
Tips and Expert Advice for Mastering Fraction Division
Mastering fraction division doesn't have to be a daunting task. With the right approach and a few handy tips, you can tackle these problems with confidence. Here's some expert advice to help you on your way:
-
Solidify Your Foundation: Before diving into division, make sure you have a strong grasp of the basics: understanding what a fraction represents, identifying numerators and denominators, and simplifying fractions. A solid foundation will make the more complex operations much easier to understand. Practice simplifying fractions regularly to build your proficiency. Use visual aids like fraction bars to reinforce your understanding of fraction equivalence.
-
Master Multiplication First: Fraction division relies heavily on multiplication. Ensure you are comfortable multiplying fractions before tackling division. Remember, multiplying fractions involves multiplying the numerators and multiplying the denominators. Regular practice with multiplication will build your confidence and speed. Try creating your own fraction multiplication problems to challenge yourself.
-
Visualize the Process: As we discussed earlier, try to visualize what it means to divide fractions. Use diagrams, drawings, or real-world examples to make the concept more concrete. Visualizing the process can help you understand why you're multiplying by the reciprocal and how the fractions are being divided. For example, think about sharing a pizza with a group of friends and dividing the slices into smaller portions.
-
Practice, Practice, Practice: The key to mastering any mathematical skill is practice. Work through a variety of fraction division problems, starting with simple ones and gradually increasing the difficulty. The more you practice, the more comfortable you'll become with the process. Use online resources, textbooks, or worksheets to find a wide range of practice problems.
-
Break Down Complex Problems: If you encounter a complex fraction division problem, break it down into smaller, more manageable steps. This will make the problem less intimidating and easier to solve. For example, if you have multiple fractions to divide, tackle them one at a time.
-
Don't Be Afraid to Ask for Help: If you're struggling with fraction division, don't hesitate to ask for help from a teacher, tutor, or friend. Sometimes, a different explanation or perspective can make all the difference. There are also plenty of online resources available, such as video tutorials and interactive exercises.
-
Use Real-World Examples: Connect fraction division to real-world situations to make it more meaningful and relevant. For example, think about dividing a recipe in half or sharing a bag of candies with a group of friends. By applying fraction division to everyday scenarios, you'll gain a better understanding of its practical applications.
Frequently Asked Questions (FAQ) About Dividing 4/3 by 2
Q: Why do we multiply by the reciprocal instead of dividing directly? A: Multiplying by the reciprocal is a shortcut that achieves the same result as dividing by a fraction. It's based on the mathematical principle that division is the inverse operation of multiplication. It's often easier to perform multiplication than division, especially with fractions.
Q: What if I have a mixed number instead of a fraction? A: Convert the mixed number into an improper fraction before dividing. For example, if you have 1 1/2, convert it to 3/2 before proceeding with the division.
Q: Can I use a calculator to divide fractions? A: Yes, calculators can be helpful for dividing fractions, but it's important to understand the underlying concepts. Don't rely solely on calculators without understanding the process.
Q: How do I divide a fraction by a whole number? A: Rewrite the whole number as a fraction by placing it over 1, then multiply the first fraction by the reciprocal of the second fraction.
Q: What are some common mistakes to avoid when dividing fractions? A: Common mistakes include forgetting to find the reciprocal, multiplying numerators without denominators (or vice versa), and not simplifying the final answer. Double-check your work to avoid these errors.
Conclusion
Dividing 4/3 by 2 might have seemed a bit mysterious at first, but by understanding the concept of reciprocals and practicing the steps involved, it becomes a manageable task. Remember that dividing by a number is the same as multiplying by its reciprocal. With a solid understanding of fractions, visualization techniques, and plenty of practice, you can conquer fraction division with confidence.
Now that you've mastered this concept, why not put your skills to the test? Try tackling some more complex fraction division problems or explore real-world applications where you can use your newfound knowledge. Share your insights with friends, family, or fellow students, and help them unlock the secrets of fraction division. The world of fractions is now yours to explore! Go ahead, conquer those fractions!
Latest Posts
Latest Posts
-
How Many Ma Is 1 Amp
Nov 08, 2025
-
What Are 2 Reactants Needed For Cellular Respiration
Nov 08, 2025
-
Show Me A Pictures Of Dinosaurs
Nov 08, 2025
-
How To Find The Least Common Denominator In Fractions
Nov 08, 2025
-
Seven Letter Words Starting With O
Nov 08, 2025
Related Post
Thank you for visiting our website which covers about 4/3 Divided By 2 In Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.