3 Out Of 70 As A Percentage
catholicpriest
Nov 09, 2025 · 10 min read
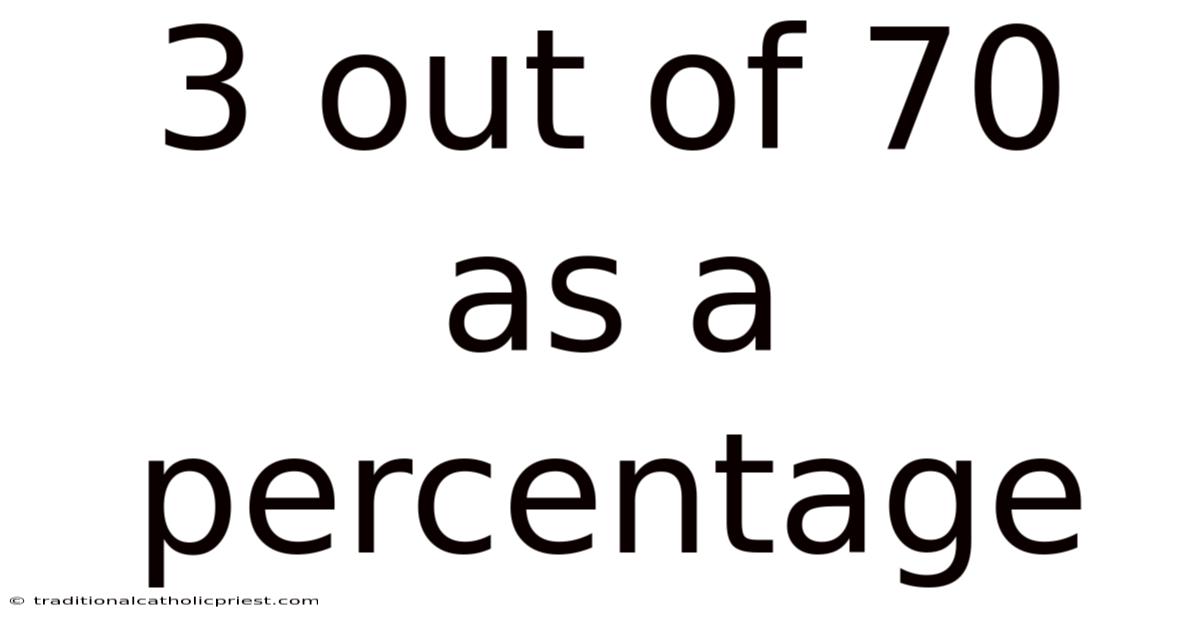
Table of Contents
Have you ever stopped to consider how frequently percentages appear in everyday life? From calculating discounts while shopping to understanding statistics in the news, percentages are an essential tool for making sense of the world around us. Understanding how to calculate a percentage, such as figuring out 3 out of 70 as a percentage, can give you a clearer insight into many situations.
Calculating percentages is more than just an academic exercise; it's a practical skill that empowers you to make informed decisions. Whether you're a student trying to understand your grades or a professional analyzing business data, knowing how to work with percentages will help you navigate various challenges with confidence. In this article, we will delve into the simple steps needed to convert 3 out of 70 as a percentage and explore the real-world applications of this fundamental skill.
Calculating a Percentage: The Basics
Percentages are a way of expressing a number as a fraction of 100. The term "percent" comes from the Latin per centum, meaning "out of one hundred." Understanding this basic concept is crucial for grasping how to calculate percentages in various contexts. When we say something is "50 percent," we mean 50 out of every 100, or half of the total.
Definition of Percentage
A percentage is a ratio or a fraction expressed as a part of 100. It is a dimensionless number, meaning it doesn't have any units attached to it. The symbol for percent is %, which is often used in conjunction with a numerical value to indicate the proportion. For example, 25% means 25 out of 100.
The Formula for Calculating Percentages
The basic formula to calculate a percentage is:
Percentage = (Part / Whole) × 100
Here, "Part" refers to the specific amount you're interested in, and "Whole" refers to the total amount. By dividing the part by the whole and then multiplying by 100, you convert the fraction into a percentage.
Historical Context of Percentages
The use of percentages dates back to ancient Rome, where calculations were often made in terms of fractions of 100. However, the modern concept of percentage became more formalized during the Renaissance period, with the growth of commerce and the need for standardized ways to calculate interest rates, taxes, and profits. Over time, percentages have become an indispensable part of mathematics, finance, and everyday life.
Converting Fractions to Percentages
To convert a fraction to a percentage, you simply divide the numerator (the top number) by the denominator (the bottom number) and then multiply the result by 100. For example, to convert the fraction 1/4 to a percentage, you would divide 1 by 4, which equals 0.25. Multiplying 0.25 by 100 gives you 25%, meaning 1/4 is equal to 25%. This same method applies to any fraction you want to convert into a percentage.
Why Percentages Are Important
Percentages are vital because they provide a standardized way to compare different proportions and quantities. They simplify the process of understanding relative values, making it easier to interpret data and make informed decisions. For example, it's easier to compare two test scores when they are expressed as percentages rather than raw scores. Percentages also play a crucial role in financial calculations, statistical analysis, and various other fields where proportional comparisons are necessary.
Calculating 3 Out of 70 as a Percentage: A Step-by-Step Guide
Now that we understand the basics of percentages, let's apply this knowledge to calculate 3 out of 70 as a percentage. This specific calculation is a practical example that demonstrates how the percentage formula works in a real-world scenario.
Step 1: Identify the "Part" and the "Whole"
In the context of calculating 3 out of 70 as a percentage, the "Part" is 3, and the "Whole" is 70. The "Part" represents the specific quantity we are interested in, while the "Whole" represents the total quantity.
Step 2: Apply the Percentage Formula
Using the percentage formula:
Percentage = (Part / Whole) × 100
Substitute the values:
Percentage = (3 / 70) × 100
Step 3: Perform the Division
Divide 3 by 70:
3 ÷ 70 ≈ 0.042857
Step 4: Multiply by 100
Multiply the result by 100 to convert it to a percentage:
- 042857 × 100 ≈ 4.2857%
Step 5: Round to the Desired Precision
Depending on the context, you may need to round the percentage to a certain number of decimal places. For example, rounding to two decimal places gives:
- 29%
Therefore, 3 out of 70 as a percentage is approximately 4.29%.
Example Scenarios
To further illustrate this calculation, consider the following examples:
- Grading: If a student scores 3 out of 70 on a quiz, their score as a percentage is approximately 4.29%.
- Survey Results: If a survey finds that 3 out of 70 people prefer a certain product, then approximately 4.29% of the respondents favor that product.
- Resource Allocation: If a project allocates 3 units of resources out of a total of 70, then approximately 4.29% of the resources are allocated to that particular task.
These examples demonstrate the versatility of calculating percentages in various real-world situations. Understanding how to perform this calculation allows you to interpret data and make informed decisions effectively.
Trends and Latest Developments in Percentage Usage
The use of percentages continues to evolve with technological advancements and changing data landscapes. Here are some of the latest trends and developments in how percentages are being used today:
Data Visualization
Percentages are increasingly used in data visualization to present information in a clear and understandable manner. Charts, graphs, and infographics often use percentages to show proportions and comparisons, making complex data accessible to a broader audience. Tools like Tableau, Power BI, and Google Data Studio enable users to create interactive dashboards that dynamically display percentages, providing real-time insights.
Statistical Analysis
In statistical analysis, percentages are used to summarize and interpret data sets. They are often used in hypothesis testing, confidence intervals, and regression analysis to draw conclusions about populations based on sample data. The use of statistical software like R and Python has made it easier to perform complex calculations and visualize percentage-based trends.
Financial Modeling
Percentages are a fundamental component of financial modeling, used to calculate returns on investment, interest rates, and growth rates. Financial analysts use percentages to assess the performance of companies, evaluate investment opportunities, and forecast future financial outcomes. Spreadsheets like Microsoft Excel and Google Sheets are widely used for creating financial models that rely heavily on percentage calculations.
E-commerce and Marketing
In e-commerce and marketing, percentages are used to track conversion rates, click-through rates, and customer engagement. Marketers use percentages to measure the effectiveness of their campaigns and optimize their strategies for better results. A/B testing, which involves comparing two versions of a webpage or advertisement, often relies on percentage differences to determine which version performs better.
Public Health
Percentages are used in public health to track disease prevalence, vaccination rates, and health outcomes. Public health officials use percentages to monitor trends, identify risk factors, and implement interventions to improve population health. Data visualization tools and statistical analysis software are used to present and interpret percentage-based health data.
Professional Insights
The consistent use of percentages across various industries highlights their importance in decision-making and strategic planning. As data becomes more accessible and sophisticated, the ability to calculate and interpret percentages will remain a critical skill for professionals in all fields.
Tips and Expert Advice for Accurate Percentage Calculations
To ensure accurate percentage calculations and effective use of percentages, consider the following tips and expert advice:
Double-Check Your Data
Always double-check the data you are using to ensure that the "Part" and the "Whole" are correctly identified. Errors in the initial data can lead to significant inaccuracies in the resulting percentage.
- Example: If you are calculating the percentage of sales from a particular region, make sure you have the correct total sales for that region and the correct overall sales figure for the company.
Understand the Context
Consider the context in which you are using the percentage. The interpretation of a percentage can vary depending on the situation.
- Example: A 5% increase in sales might be considered excellent in a stable market but only moderate in a rapidly growing market.
Use Calculators and Tools
Take advantage of calculators, spreadsheets, and other tools to perform percentage calculations accurately. These tools can help minimize errors and save time.
- Example: Use Microsoft Excel or Google Sheets to create formulas that automatically calculate percentages based on your data.
Be Consistent with Rounding
When rounding percentages, be consistent with the number of decimal places you use. This ensures that comparisons between different percentages are fair and accurate.
- Example: If you are comparing multiple percentages, round all of them to the same number of decimal places (e.g., two decimal places).
Avoid Common Mistakes
Be aware of common mistakes when calculating percentages, such as confusing the "Part" and the "Whole" or forgetting to multiply by 100.
- Example: Make sure you are dividing the specific quantity you are interested in by the total quantity, and always multiply the result by 100 to convert it to a percentage.
Seek Expert Advice
If you are unsure about how to calculate or interpret a percentage in a particular situation, seek advice from a professional with expertise in the relevant field.
- Example: Consult with a financial analyst for advice on calculating investment returns or a statistician for guidance on interpreting survey results.
By following these tips and seeking expert advice when needed, you can ensure that you are using percentages accurately and effectively in your analyses and decision-making processes.
Frequently Asked Questions (FAQ)
Q: How do I convert a percentage back to a fraction?
A: To convert a percentage back to a fraction, divide the percentage by 100 and simplify the resulting fraction. For example, to convert 25% to a fraction, divide 25 by 100 to get 0.25, which is equal to 1/4.
Q: What is the difference between percentage increase and percentage decrease?
A: Percentage increase refers to the relative increase in a quantity, calculated as [(New Value - Old Value) / Old Value] × 100. Percentage decrease refers to the relative decrease in a quantity, calculated as [(Old Value - New Value) / Old Value] × 100.
Q: How do I calculate the percentage of a total?
A: To calculate the percentage of a total, divide the specific quantity you are interested in by the total quantity and multiply the result by 100. For example, if you want to find what percentage 30 is of 200, calculate (30 / 200) × 100, which equals 15%.
Q: Can a percentage be greater than 100%?
A: Yes, a percentage can be greater than 100% when the "Part" is larger than the "Whole." This often occurs in situations involving growth or increase. For example, if a company's sales increase by 150% compared to the previous year, it means the sales have more than doubled.
Q: How are percentages used in everyday life?
A: Percentages are used in many everyday situations, such as calculating discounts while shopping, understanding interest rates on loans, interpreting statistics in the news, and determining grades in school.
Conclusion
In summary, understanding how to calculate 3 out of 70 as a percentage is a valuable skill that can be applied in numerous real-world scenarios. By following the simple steps outlined in this article—identifying the "Part" and the "Whole," applying the percentage formula, performing the division, and multiplying by 100—you can accurately convert any fraction into a percentage. Whether you're a student, a professional, or simply someone looking to improve your understanding of quantitative data, mastering percentage calculations will empower you to make more informed decisions.
Now that you have a solid understanding of percentages, take the next step and apply this knowledge in your daily life. Practice calculating percentages in different contexts, and explore the various tools and resources available to help you streamline your calculations. Share this article with your friends and colleagues, and let's continue to enhance our understanding of this essential mathematical concept together.
Latest Posts
Latest Posts
-
What Is The Meaning Of Dime A Dozen
Nov 09, 2025
-
6 Letter Words That Begin With D
Nov 09, 2025
-
Who Is The Chief Legal Officer Of Illinois
Nov 09, 2025
-
What Is 1 8 1 4 As A Fraction
Nov 09, 2025
-
Alice In Wonderland Book Read Online
Nov 09, 2025
Related Post
Thank you for visiting our website which covers about 3 Out Of 70 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.