25 Is What Percent Of 5
catholicpriest
Nov 18, 2025 · 13 min read
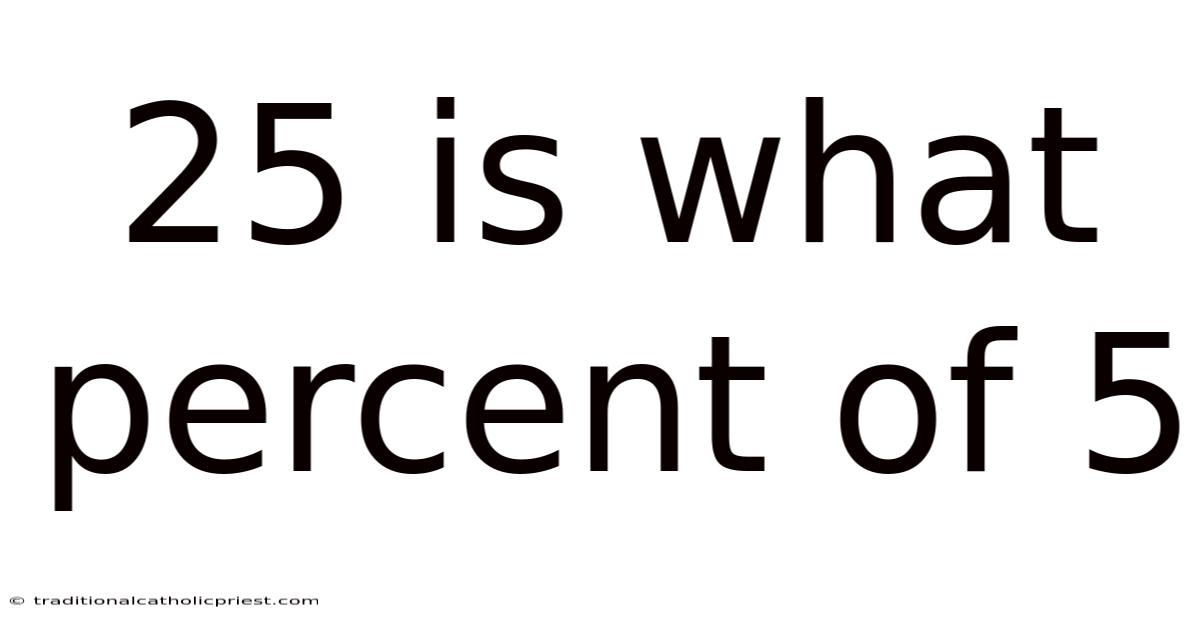
Table of Contents
Imagine you're at a farmers market, eyeing a basket of vibrant, juicy strawberries. The sign says "$5 a basket," but you only have $25 in your wallet. You wonder, "Can I buy multiple baskets?" The simple calculation of how much of your total money is represented by the cost of one basket is essentially the same principle behind calculating percentages. It's a practical way to understand proportions and relative amounts in everyday situations.
Or picture this: you're a student who just received a test back. You got 25 questions right out of a possible 5. How well did you do? Expressing this as a percentage gives you an immediate sense of your performance compared to the total possible score. Understanding how to calculate "25 is what percent of 5" isn't just about math; it's about making sense of the world around you, from budgeting to understanding statistics.
Understanding the Basics of Percentage Calculations
Percentages are fundamental in mathematics and daily life. They provide a standardized way to express proportions and compare different quantities relative to a whole. To truly grasp how to calculate what percentage one number is of another, we need to define the terms and understand the underlying formula.
Defining Percentage
A percentage is a way of expressing a number as a fraction of 100. The term "percent" comes from the Latin per centum, meaning "per hundred." So, when we say "X percent," we mean X out of every 100. This standardization allows for easy comparison of different fractions or ratios. For example, saying that 20% of a group prefers coffee is immediately understandable, regardless of the group's size.
The Formula for Calculating Percentage
The basic formula to calculate what percentage a number (the part) is of another number (the whole) is:
Percentage = (Part / Whole) * 100
In the question "25 is what percent of 5?", 25 is the 'part', and 5 is the 'whole'.
Historical Context
The concept of percentages dates back to ancient Rome. As the Roman Empire expanded, taxes were often calculated as fractions of assets or goods. These fractions were frequently expressed as hundredths, similar to our modern percentages. However, the widespread use of percentages as we know them today began in the Middle Ages with the growth of commerce and the need for standardized financial calculations. Merchants, bankers, and scholars developed methods to calculate interest, profits, and taxes based on proportions, laying the groundwork for the percentage calculations we use today.
Real-World Applications
Understanding percentages is crucial in numerous real-world contexts. In finance, percentages are used to calculate interest rates, investment returns, and loan payments. In retail, discounts and sales are expressed as percentages. In science, percentages are used to express concentrations of solutions and analyze experimental data. Moreover, understanding percentages is essential for interpreting statistical data, such as survey results and demographic information. Whether you're figuring out a tip at a restaurant, comparing investment options, or analyzing scientific data, percentages provide a versatile tool for understanding and interpreting the world around you.
Common Misconceptions
One common mistake is confusing the part and the whole in percentage calculations. It's essential to correctly identify which number represents the total or reference value (the whole) and which number represents the portion of that total (the part). Another misconception is thinking that a percentage can exceed 100%. While it's true that a part can be larger than the originally defined whole (leading to results over 100% when comparing to that original whole), it's crucial to understand the context and what the percentage represents in such cases.
Calculating "25 is What Percent of 5": A Comprehensive Guide
Now, let's dive into the specific calculation of "25 is what percent of 5". This might seem counter-intuitive at first because 25 is larger than 5. However, the question is valid and can be answered using the percentage formula.
Step-by-Step Calculation
-
Identify the Part and the Whole:
- Part: 25
- Whole: 5
-
Apply the Formula:
Percentage = (Part / Whole) * 100
Percentage = (25 / 5) * 100
-
Perform the Division:
25 / 5 = 5
-
Multiply by 100:
5 * 100 = 500
-
Result:
25 is 500% of 5.
Interpretation
The result, 500%, means that 25 is five times greater than 5. In other words, 25 represents 500% of the value of 5. This kind of calculation is particularly useful when comparing a value to a baseline or reference point, even if the value is much larger than the baseline.
Visual Representation
To visualize this, imagine you have five apples (representing the 'whole' of 5). Now, imagine you have five times that many apples. That would be 25 apples (representing the 'part' of 25). So, you have 500% of the original amount of apples.
Similar Examples
To reinforce understanding, let's look at a couple of similar examples:
-
Example 1: 10 is what percent of 2?
- Part: 10
- Whole: 2
- Percentage = (10 / 2) * 100 = 5 * 100 = 500%
So, 10 is 500% of 2.
-
Example 2: 15 is what percent of 3?
- Part: 15
- Whole: 3
- Percentage = (15 / 3) * 100 = 5 * 100 = 500%
So, 15 is 500% of 3.
These examples illustrate that when the 'part' is larger than the 'whole', the percentage will be greater than 100%.
Practical Applications
While the calculation itself is straightforward, understanding when and why you might need to perform such a calculation is crucial. Here are a few practical scenarios:
- Business Growth: A small business might measure its revenue growth compared to its initial capital. If a business starts with $5,000 and now has a revenue of $25,000, the revenue is 500% of the initial capital.
- Investment Returns: Investors might compare their portfolio's current value to their initial investment. If an investment of $500 grows to $2,500, the current value is 500% of the initial investment.
- Scientific Experiments: In some experiments, scientists might compare the final yield of a reaction to the amount of catalyst used. If 5 grams of catalyst result in 25 grams of product, the product yield is 500% of the catalyst amount.
Common Pitfalls
One common error is misinterpreting the result. A percentage greater than 100% simply means that the 'part' is larger than the 'whole'. It doesn't necessarily indicate a mistake, but it's important to understand the context. Another pitfall is incorrectly identifying the 'part' and the 'whole'. Always double-check which number represents the total or reference value.
Current Trends and Developments in Percentage Use
Percentages have evolved alongside technological and societal advancements. Modern data analysis, digital tools, and economic shifts have influenced how percentages are used and interpreted. Here's a look at some current trends and developments:
Data Visualization and Infographics
In the age of big data, percentages are frequently used in data visualization and infographics to present complex information in an accessible format. Visual aids like pie charts, bar graphs, and percentage-based progress bars help audiences quickly grasp the significance of data. For example, news organizations often use infographics to illustrate the percentage of the population affected by a particular policy or event. Businesses use them to show market share, customer demographics, and sales growth. The key is to present percentages visually so they are easily understood at a glance.
Digital Tools and Calculators
The proliferation of digital tools and calculators has made percentage calculations more accessible than ever. Online calculators, spreadsheet software, and mobile apps can quickly perform complex percentage calculations, reducing the risk of human error. These tools are invaluable for students, professionals, and anyone needing to work with percentages regularly. Moreover, many e-commerce platforms and financial websites incorporate percentage calculators to help users estimate discounts, interest rates, and other financial metrics.
Economic and Financial Analysis
Percentages play a crucial role in economic and financial analysis. Economists use percentages to track inflation rates, unemployment rates, and GDP growth. Financial analysts use percentages to evaluate investment performance, assess risk, and analyze financial statements. Understanding how to interpret these percentage-based metrics is essential for making informed decisions in the financial world. For example, changes in interest rates (expressed as percentages) can significantly impact investment strategies and consumer spending.
Statistical Analysis
In statistical analysis, percentages are used to summarize and compare data sets. Researchers use percentages to calculate proportions, probabilities, and confidence intervals. Understanding percentages is essential for interpreting statistical results and drawing meaningful conclusions. For example, a political poll might report that 60% of respondents support a particular candidate, with a margin of error of ±3%. This means that the true percentage of support is likely between 57% and 63%.
Machine Learning and AI
Even in advanced fields like machine learning and artificial intelligence, percentages are used to evaluate model performance. Accuracy, precision, and recall are often expressed as percentages, providing a standardized way to compare different models. For example, a machine learning model designed to detect fraud might have an accuracy of 95%, meaning it correctly identifies 95% of fraudulent transactions.
Professional Insights
One professional insight is the importance of understanding the context behind percentages. A percentage can be misleading if it's not presented with sufficient background information. For example, a 100% increase in sales might sound impressive, but if the initial sales volume was very low, the increase might not be as significant as it appears. Similarly, a small percentage change in a large population can have a substantial impact. Therefore, it's crucial to consider the absolute numbers alongside the percentages to get a complete picture.
Practical Tips and Expert Advice for Percentage Calculations
Mastering percentage calculations involves not just knowing the formulas but also understanding how to apply them effectively in various situations. Here are some practical tips and expert advice:
Simplify Before Calculating
Before plugging numbers into a formula, simplify the problem if possible. For example, if you're calculating 25% of 80, recognize that 25% is the same as 1/4. Therefore, you can simply divide 80 by 4 to get the answer (20). This approach can save time and reduce the risk of errors.
Use Benchmarks
Familiarize yourself with common percentage benchmarks. Knowing that 50% is one-half, 25% is one-quarter, and 10% is one-tenth can help you quickly estimate percentages without a calculator. For example, if you need to calculate 52% of 100, you know it will be slightly more than half, so around 50. These benchmarks provide a mental framework for understanding and estimating percentages.
Convert Percentages to Decimals
To perform calculations, convert percentages to decimals by dividing by 100. For example, 30% becomes 0.30, 75% becomes 0.75, and so on. Multiplying by the decimal equivalent is often easier than working directly with percentages. This is especially useful when dealing with more complex calculations or when using calculators or spreadsheets.
Estimate and Check Your Answers
Before finalizing a calculation, estimate the answer to ensure your result is reasonable. For example, if you're calculating 15% of 200, estimate that 10% of 200 is 20, so 15% should be slightly more than that. This helps you catch any major errors in your calculations.
Understand Percentage Change
When calculating percentage change (increase or decrease), use the formula:
Percentage Change = ((New Value - Old Value) / Old Value) * 100
Be careful to use the correct 'Old Value' as the denominator. For example, if a price increases from $20 to $25, the percentage change is ((25 - 20) / 20) * 100 = 25%.
Practice Regularly
Like any skill, proficiency in percentage calculations comes with practice. Work through various examples and real-world problems to build your confidence and intuition. Use online resources, textbooks, and practice quizzes to reinforce your understanding. The more you practice, the more comfortable you'll become with percentage calculations.
Use Technology Wisely
While digital tools can be helpful, don't rely on them blindly. Understand the underlying concepts and formulas so you can perform calculations manually when necessary. Technology should be used to enhance your understanding, not replace it.
Expert Advice
One piece of expert advice is to always double-check your work, especially in high-stakes situations like financial calculations. A small error in a percentage calculation can have significant consequences. Another tip is to be mindful of the context. Percentages can be easily misinterpreted if they're not presented with sufficient background information. Always consider the absolute numbers alongside the percentages to get a complete picture.
Frequently Asked Questions (FAQ) About Percentage Calculations
Q: How do I convert a fraction to a percentage?
A: Divide the numerator by the denominator, then multiply by 100. For example, to convert 3/4 to a percentage, calculate (3 ÷ 4) * 100 = 75%.
Q: How do I find the original value if I know a percentage of it?
A: Divide the known value by the percentage (expressed as a decimal). For example, if 20% of a number is 50, then the original number is 50 ÷ 0.20 = 250.
Q: What's the difference between percentage increase and percentage decrease?
A: Percentage increase is calculated as ((New Value - Old Value) / Old Value) * 100, where the New Value is greater than the Old Value. Percentage decrease is calculated the same way, but the New Value is less than the Old Value, resulting in a negative percentage.
Q: How do I calculate multiple percentages of a number?
A: Calculate each percentage separately and then add or subtract the results as needed. For example, to calculate 10% and 20% of 100, first find 10% of 100 (which is 10) and then find 20% of 100 (which is 20).
Q: Can a percentage be greater than 100%?
A: Yes, a percentage can be greater than 100% if you're comparing a value to a baseline or reference point that is smaller than the value itself. This simply means that the value is more than the original baseline.
Conclusion
Understanding how to calculate "25 is what percent of 5" and other percentage-related problems is more than just an academic exercise; it's a practical skill that enhances your ability to interpret and analyze the world around you. From managing personal finances to understanding complex data sets, percentages provide a standardized way to express proportions and make meaningful comparisons.
By mastering the basic formulas, understanding the real-world applications, and practicing regularly, you can develop a strong foundation in percentage calculations. Remember to simplify problems when possible, use benchmarks to estimate answers, and always double-check your work.
Now that you have a comprehensive understanding of percentage calculations, take the next step and apply your knowledge to real-world scenarios. Whether you're calculating discounts, analyzing investment returns, or interpreting statistical data, the ability to work with percentages will empower you to make more informed decisions. Don't hesitate to use online resources and digital tools to enhance your learning, but always remember the underlying concepts and formulas. Start practicing today and unlock the power of percentages!
Latest Posts
Latest Posts
-
How Do I Find The Slope Of A Tangent Line
Nov 18, 2025
-
How Does A 2 Stroke Diesel Work
Nov 18, 2025
-
When To Use Biot Savart Law
Nov 18, 2025
-
What Does The Number 11 Represent
Nov 18, 2025
-
Can You Have Accuracy Without Precision
Nov 18, 2025
Related Post
Thank you for visiting our website which covers about 25 Is What Percent Of 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.