1 Is What Percent Of 3
catholicpriest
Nov 21, 2025 · 12 min read
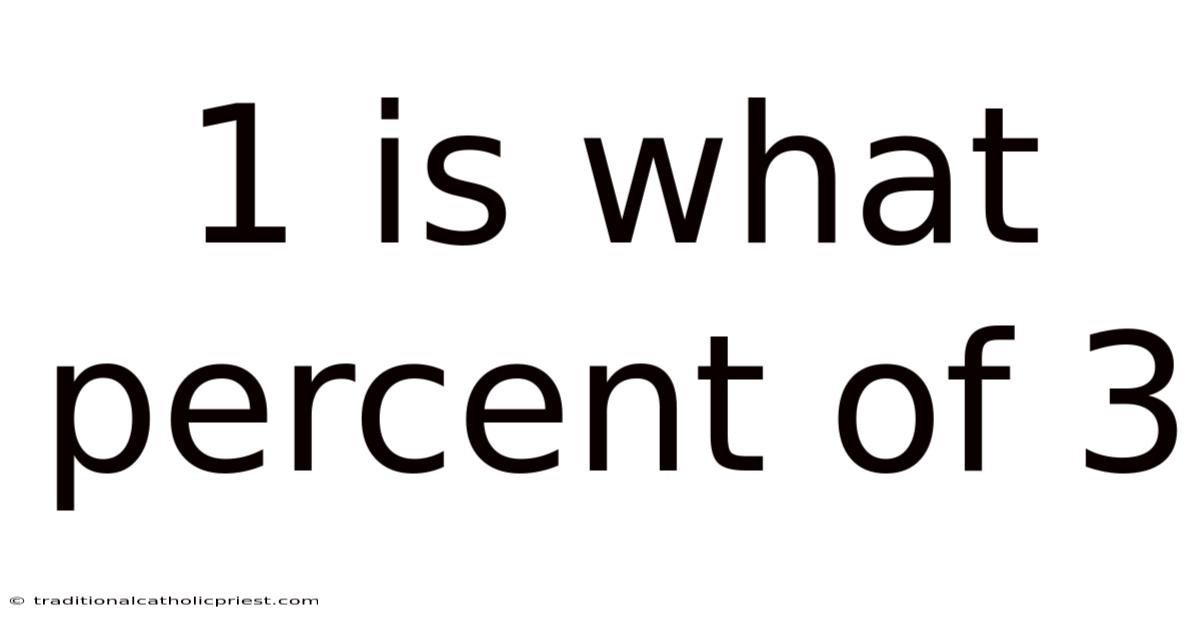
Table of Contents
Imagine you're baking a cake, and the recipe calls for 3 cups of flour. You realize you only have 1 cup. What portion of the recipe's flour do you actually have? This simple scenario highlights a common need: understanding percentages. Percentages help us express parts of a whole, compare quantities, and make informed decisions in everyday life, from cooking to finance.
Calculating "1 is what percent of 3" is a fundamental math problem with broad applications. Whether you're figuring out discounts, analyzing statistics, or just trying to understand proportions, knowing how to calculate percentages accurately is essential. In this article, we'll break down the concept of percentages, explore the specific calculation of "1 is what percent of 3", and delve into practical applications to help you master this valuable skill.
Main Subheading
The question "1 is what percent of 3" is a classic percentage problem that requires understanding the relationship between a part (1) and a whole (3). Percentages are a way of expressing a number as a fraction of 100. The term "percent" comes from the Latin per centum, meaning "per hundred." Therefore, when we ask what percent one number is of another, we're essentially asking how many hundredths of the second number the first number represents.
Understanding this concept is crucial not only for solving mathematical problems but also for interpreting data in various real-world scenarios. For example, if a company reports that its sales increased by 1% compared to last year, it means that for every 100 units sold last year, they sold 101 units this year. Percentages provide a standardized way to compare quantities, making them indispensable in fields like finance, statistics, and even everyday decision-making. In the following sections, we will explore the underlying mathematical principles and practical applications of this concept.
Comprehensive Overview
To understand "1 is what percent of 3," it's essential to grasp the basic principles of percentages. A percentage is essentially a fraction or a ratio expressed as a portion of 100. The formula to calculate what percent one number (the part) is of another number (the whole) is:
(Part / Whole) * 100 = Percentage
In this formula:
- Part is the number we want to express as a percentage of the whole.
- Whole is the total or reference number.
- Percentage is the result of the calculation, expressed as a percent.
The Foundation of Percentage Calculation
The formula works because it first finds the decimal equivalent of the fraction (Part / Whole). Multiplying this decimal by 100 converts it into a percentage, which is easier to understand and compare. For example, if we want to find what percent 20 is of 100, we would calculate (20 / 100) * 100, which equals 20%.
Applying the Formula to "1 is what percent of 3"
Using the formula, we can easily calculate what percent 1 is of 3:
- Identify the Part and the Whole:
- Part = 1
- Whole = 3
- Apply the Formula:
- (1 / 3) * 100 = Percentage
- Calculate:
- 1 / 3 = 0.3333...
- 0.3333... * 100 = 33.33...%
Therefore, 1 is approximately 33.33% of 3. The repeating decimal emphasizes that the percentage is an approximation, and in practical contexts, it's often rounded to a suitable number of decimal places.
Historical Context and Significance
The concept of percentages dates back to ancient Rome, where calculations were often made in terms of hundredths. However, the modern use of the percent sign (%) and the standardization of percentage calculations emerged during the Renaissance. The need for standardized financial calculations and comparisons drove the widespread adoption of percentages in commerce, finance, and science.
Percentages provide a universal language for expressing proportions, making it easier to compare data across different scales. For example, expressing growth rates, discounts, or error margins as percentages allows for quick and intuitive comparisons, regardless of the absolute numbers involved. The ability to understand and calculate percentages is a fundamental skill that enhances quantitative literacy and decision-making across various domains.
Understanding Proportions and Ratios
Percentages are closely related to proportions and ratios, which are other ways of expressing the relationship between two quantities. A ratio compares two quantities, while a proportion states that two ratios are equal. Understanding these concepts can provide additional context and insights into percentage calculations.
For example, the ratio of 1 to 3 can be written as 1:3, indicating that for every one unit of the first quantity, there are three units of the second quantity. When we calculate that 1 is 33.33% of 3, we are essentially expressing the same relationship in terms of hundredths. The proportion could be written as 1/3 = x/100, where x represents the percentage we are trying to find.
Practical Examples in Everyday Life
The application of percentages extends to numerous aspects of daily life:
- Finance: Calculating interest rates, investment returns, and loan payments.
- Retail: Determining discounts, markups, and sales tax.
- Health: Understanding body fat percentage, medication dosages, and nutritional information.
- Statistics: Interpreting survey results, demographic data, and scientific findings.
For example, if a store offers a 20% discount on an item priced at $50, the discount amount is (20/100) * 50 = $10. The sale price is then $50 - $10 = $40. In each of these scenarios, the ability to calculate percentages accurately is essential for making informed decisions and understanding the world around us.
Trends and Latest Developments
In recent years, the use of percentages has evolved with advancements in data analytics and technology. Here are some notable trends and developments:
Increased Use in Data Visualization
Percentages are increasingly used in data visualization tools to present complex information in an accessible format. Charts and graphs often display data as percentages to highlight proportions and trends. For example, pie charts use percentages to show how different categories contribute to a whole, while bar graphs may use percentages to compare performance across different groups.
Data visualization tools often include features that automatically calculate and display percentages, making it easier for users to interpret data and draw meaningful conclusions. This trend underscores the importance of understanding percentages in the age of big data and data-driven decision-making.
Application in Machine Learning and AI
Percentages play a critical role in machine learning and artificial intelligence (AI) algorithms. Machine learning models often use percentages to express confidence levels, accuracy rates, and error margins. For example, a classification model might predict the probability that an email is spam, expressing its confidence as a percentage.
AI-powered systems also use percentages to optimize performance and make decisions based on probabilistic reasoning. Understanding how percentages are used in these contexts is becoming increasingly important for professionals in data science, software engineering, and related fields.
Growth in Financial Literacy Education
There is a growing emphasis on financial literacy education, which includes teaching individuals how to understand and calculate percentages in financial contexts. Many educational programs and online resources focus on helping people make informed decisions about budgeting, saving, investing, and managing debt.
Understanding percentages is a key component of financial literacy, as it enables individuals to evaluate interest rates, calculate returns on investments, and compare financial products. This trend reflects a broader recognition of the importance of quantitative skills in navigating the complexities of modern financial systems.
Use in Social and Political Polling
Percentages are fundamental to social and political polling, where they are used to express public opinion, voting preferences, and demographic trends. Pollsters use statistical methods to estimate the percentage of a population that holds a particular view or supports a specific candidate.
The accuracy and reliability of polling data depend on understanding the principles of percentage calculation and statistical inference. Poll results are often presented with margin of error, which is also expressed as a percentage, indicating the range within which the true population value is likely to fall.
Professional Insights
From a professional standpoint, understanding percentages requires not only computational skills but also critical thinking and contextual awareness. Professionals in finance, marketing, and analytics need to interpret percentages accurately and communicate their findings effectively to stakeholders.
For example, a marketing manager might analyze the percentage change in website traffic after launching a new campaign, using this information to assess the campaign's effectiveness and make adjustments as needed. Similarly, a financial analyst might evaluate the percentage return on an investment portfolio, comparing it to benchmark indices and assessing risk-adjusted performance.
Staying current with trends in data visualization, machine learning, and financial literacy can enhance one's ability to use percentages effectively in professional contexts. Continuous learning and skill development are essential for leveraging the power of percentages in data-driven decision-making.
Tips and Expert Advice
Mastering percentage calculations and applications requires a combination of theoretical knowledge and practical skills. Here are some tips and expert advice to help you improve your understanding and proficiency:
Practice Regularly
Like any mathematical skill, proficiency in percentage calculation comes with practice. Set aside time each week to work through percentage problems, using real-world examples and scenarios. Practice can help you build confidence and develop a deeper understanding of the underlying concepts.
Use online resources, textbooks, and worksheets to find practice problems. Start with basic calculations and gradually progress to more complex applications. The more you practice, the more comfortable you will become with percentages.
Understand the Context
Percentages are often used in specific contexts, such as finance, retail, or statistics. Understanding the context is crucial for interpreting percentages accurately and making informed decisions. Take the time to learn about the terminology and conventions used in each context.
For example, in finance, it's important to understand concepts like interest rates, returns on investment, and risk-adjusted performance. In retail, understanding markups, discounts, and sales tax is essential. By understanding the context, you can better interpret percentages and apply them effectively.
Use Estimation Techniques
Estimation techniques can help you quickly approximate percentage calculations and check your work. For example, if you need to calculate 20% of 50, you can estimate by thinking of 20% as one-fifth. One-fifth of 50 is 10, so 20% of 50 is approximately 10.
Estimation techniques are particularly useful when you don't have access to a calculator or when you need to make quick decisions. By practicing estimation, you can improve your mental math skills and develop a better intuition for percentages.
Learn to Convert Between Fractions, Decimals, and Percentages
Percentages, fractions, and decimals are all ways of expressing proportions. Learning to convert between these forms can help you solve percentage problems more efficiently and understand the relationships between different quantities.
To convert a fraction to a percentage, divide the numerator by the denominator and multiply by 100. To convert a percentage to a decimal, divide by 100. To convert a decimal to a percentage, multiply by 100. By mastering these conversions, you can easily switch between different representations of proportions and solve percentage problems more effectively.
Break Down Complex Problems
Complex percentage problems can be broken down into smaller, more manageable steps. For example, if you need to calculate the final price of an item after multiple discounts and sales tax, break the problem down into individual calculations.
First, calculate the discount amount and subtract it from the original price. Then, calculate the sales tax on the discounted price and add it to find the final price. By breaking down complex problems, you can simplify the calculations and reduce the risk of errors.
Use Technology Wisely
Calculators, spreadsheets, and online tools can be valuable resources for percentage calculations. However, it's important to use technology wisely and not rely on it exclusively. Make sure you understand the underlying concepts and can perform basic calculations manually.
Technology can help you automate complex calculations, analyze large datasets, and visualize data. However, it's important to be able to verify the results and understand the limitations of the tools you are using.
Seek Feedback and Collaboration
Collaborate with others and seek feedback on your percentage calculations and applications. Discuss problems with colleagues, classmates, or mentors and ask for their input. Collaborating with others can help you identify errors, learn new techniques, and gain different perspectives.
Attending workshops, seminars, and online courses can also provide valuable opportunities to learn from experts and network with other professionals. By seeking feedback and collaboration, you can continuously improve your skills and knowledge.
FAQ
Q: What is a percentage?
A: A percentage is a way of expressing a number as a fraction of 100. It's used to show proportions and make comparisons easier.
Q: How do you calculate what percent one number is of another?
A: Use the formula: (Part / Whole) * 100 = Percentage. For example, to find what percent 1 is of 3, calculate (1 / 3) * 100.
Q: Why are percentages important?
A: Percentages are important because they provide a standardized way to compare quantities, understand proportions, and make informed decisions in various fields like finance, retail, and statistics.
Q: How can I improve my percentage calculation skills?
A: Practice regularly, understand the context, use estimation techniques, learn to convert between fractions, decimals, and percentages, break down complex problems, and use technology wisely.
Q: What are some common mistakes to avoid when calculating percentages?
A: Common mistakes include using the wrong numbers for the part and whole, not converting decimals to percentages correctly, and misunderstanding the context of the problem.
Conclusion
Understanding and calculating percentages is an essential skill with broad applications in everyday life and various professional fields. The question "1 is what percent of 3" is a fundamental example that illustrates the core principles of percentage calculation. By grasping the underlying concepts, practicing regularly, and applying practical tips, you can master percentages and enhance your quantitative literacy.
Now that you have a comprehensive understanding of how to calculate percentages, take the next step and apply this knowledge to real-world scenarios. Try calculating discounts while shopping, analyzing financial data, or interpreting statistical reports. Share your insights and experiences with others, and continue to refine your skills through practice and collaboration. Embrace the power of percentages to make informed decisions and navigate the complexities of our data-driven world. What other percentage problems can you solve today?
Latest Posts
Latest Posts
-
Arcs And Angles In A Circle
Nov 21, 2025
-
When Was The Element Krypton Discovered
Nov 21, 2025
-
How To Put Vertex Form Into Standard Form
Nov 21, 2025
-
Helper Or Suppressor Cells Are Types Of
Nov 21, 2025
-
Convert Cubic Feet To Gallons Calculator
Nov 21, 2025
Related Post
Thank you for visiting our website which covers about 1 Is What Percent Of 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.