1 And 1 2 Divided By 2
catholicpriest
Nov 25, 2025 · 11 min read
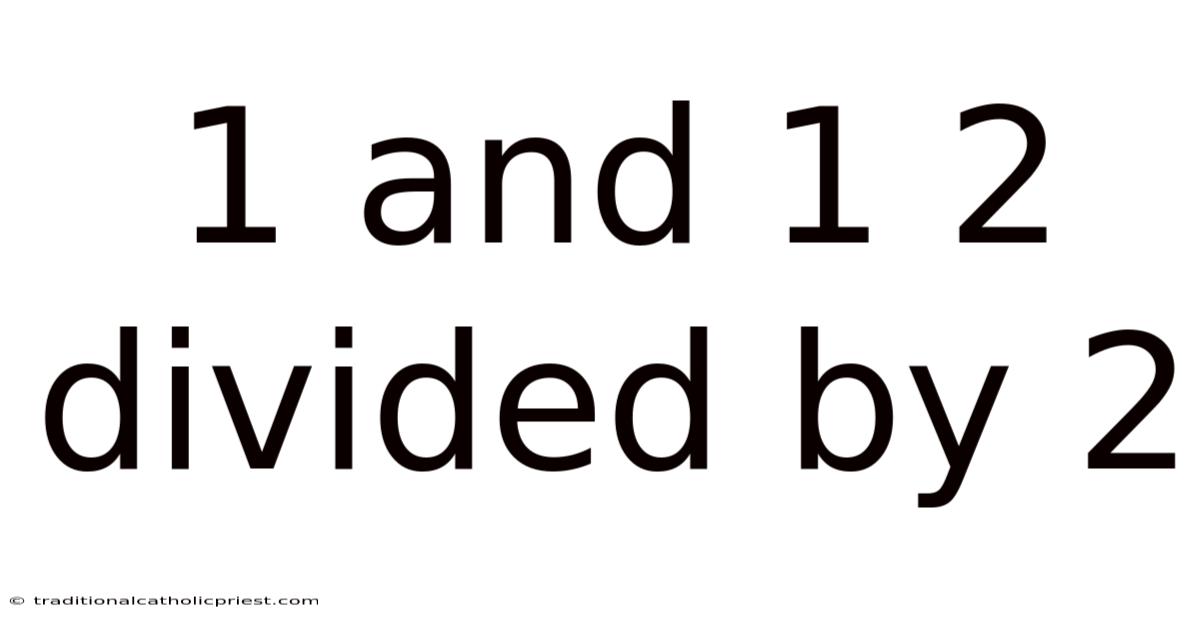
Table of Contents
Have you ever paused to consider the elegance hidden within seemingly simple arithmetic? The phrase "1 and 1/2 divided by 2" might sound straightforward, yet it opens a door to fascinating mathematical concepts and practical applications.
Imagine you're baking cookies and the recipe calls for 1 and 1/2 cups of flour, but you only want to make half the batch. Or perhaps you're splitting a 1.5-mile running route with a friend. Suddenly, this basic calculation becomes more than just numbers; it becomes a tool for everyday problem-solving. Understanding how to accurately perform this calculation is not only fundamental to math but also surprisingly useful in navigating daily life.
Understanding 1 and 1/2 Divided by 2
To truly grasp "1 and 1/2 divided by 2," we need to break it down into its core components. This simple phrase involves fractions, division, and a mix of whole numbers and fractions, commonly known as mixed numbers. Mastering this operation is not just about getting the right answer; it's about understanding the underlying principles that govern arithmetic.
At its heart, the problem "1 and 1/2 divided by 2" tests our ability to work with fractions and perform division accurately. It's a gateway to more complex mathematical concepts and a vital skill for numerous real-world applications. Whether you're a student learning the basics or someone brushing up on their math skills, this seemingly simple problem offers a valuable learning opportunity. The key lies in understanding how to convert mixed numbers into improper fractions, perform the division correctly, and interpret the result in a meaningful way.
Comprehensive Overview
The Basics of Fractions
A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates the total number of equal parts the whole is divided into. For example, in the fraction 1/2, the numerator is 1, and the denominator is 2, meaning we have one part out of two equal parts.
Mixed Numbers Explained
A mixed number is a combination of a whole number and a fraction. The mixed number "1 and 1/2" consists of the whole number 1 and the fraction 1/2. Understanding how to convert mixed numbers into improper fractions is crucial for performing arithmetic operations like division.
Converting Mixed Numbers to Improper Fractions
To convert a mixed number to an improper fraction, follow these steps:
- Multiply the whole number by the denominator of the fraction.
- Add the numerator of the fraction to the result.
- Place the sum over the original denominator.
For example, to convert "1 and 1/2" to an improper fraction:
- Multiply 1 (the whole number) by 2 (the denominator): 1 * 2 = 2.
- Add 1 (the numerator) to the result: 2 + 1 = 3.
- Place the sum (3) over the original denominator (2): 3/2.
Therefore, the improper fraction equivalent of "1 and 1/2" is 3/2. This conversion is essential because it allows us to perform division more easily.
Division with Fractions
Dividing by a number is the same as multiplying by its reciprocal. The reciprocal of a number is simply 1 divided by that number. For a fraction, the reciprocal is obtained by swapping the numerator and the denominator. For example, the reciprocal of 2 (or 2/1) is 1/2. When dividing by a fraction, you multiply by its reciprocal. This principle is fundamental to solving "1 and 1/2 divided by 2."
Step-by-Step Solution
Now that we've covered the basics, let's solve "1 and 1/2 divided by 2" step by step:
- Convert the mixed number to an improper fraction: As shown earlier, 1 and 1/2 converts to 3/2.
- Rewrite the division problem: "1 and 1/2 divided by 2" becomes 3/2 ÷ 2.
- Find the reciprocal of the divisor: The divisor is 2, which can be written as 2/1. The reciprocal of 2/1 is 1/2.
- Multiply by the reciprocal: 3/2 ÷ 2 becomes 3/2 * 1/2.
- Multiply the numerators: 3 * 1 = 3.
- Multiply the denominators: 2 * 2 = 4.
- Write the result: The result is 3/4.
Therefore, 1 and 1/2 divided by 2 equals 3/4.
Trends and Latest Developments
While the fundamental principles of arithmetic remain constant, the methods and tools we use to perform calculations are continually evolving. Here are some trends and developments in how we approach and teach basic arithmetic:
Visual Learning Tools
Educational platforms increasingly incorporate visual aids and interactive tools to help students grasp mathematical concepts. These tools often include diagrams, animations, and simulations that make abstract ideas more concrete. For example, visualizing fractions with pie charts or using interactive number lines can help students understand division and fractions more intuitively.
Gamification of Learning
Gamification involves incorporating game-like elements into the learning process to increase engagement and motivation. Math games and apps often present arithmetic problems in an engaging format, providing immediate feedback and rewards. This approach can make learning math more enjoyable and effective, especially for younger learners.
Personalized Learning Paths
Adaptive learning platforms use algorithms to tailor the learning experience to each student's individual needs and pace. These platforms assess a student's understanding of a concept and provide targeted instruction and practice based on their strengths and weaknesses. This personalized approach can help students master arithmetic skills more efficiently.
Integration of Technology
The integration of technology in education has led to the development of numerous tools and resources for learning arithmetic. Online calculators, math apps, and educational websites offer students convenient ways to practice and reinforce their skills. These resources can be particularly useful for students who need extra help or want to explore advanced topics.
Emphasis on Conceptual Understanding
Modern math education emphasizes conceptual understanding over rote memorization. Instead of simply memorizing formulas and procedures, students are encouraged to understand the underlying principles and reasoning behind mathematical concepts. This approach helps students develop a deeper and more flexible understanding of math, enabling them to apply their skills to a wider range of problems.
Real-World Applications
Connecting math to real-world applications is a key trend in math education. By showing students how arithmetic skills are used in everyday life, educators can increase their motivation and engagement. For example, using cooking recipes, budgeting scenarios, or measurement problems can help students see the relevance of math to their lives.
Professional Insights
From a professional perspective, a solid foundation in basic arithmetic is essential for numerous careers. Engineers, scientists, accountants, and financial analysts all rely on arithmetic skills to perform their jobs effectively. Even in fields that are not traditionally associated with math, such as marketing and project management, a strong understanding of arithmetic can be valuable for data analysis and decision-making. The ability to quickly and accurately perform calculations, estimate values, and interpret numerical data is a valuable asset in the workplace.
Tips and Expert Advice
Mastering "1 and 1/2 divided by 2" and similar arithmetic problems requires practice and a solid understanding of the underlying concepts. Here are some tips and expert advice to help you improve your skills:
Practice Regularly
Consistent practice is key to mastering arithmetic skills. Set aside time each day to work on math problems, even if it's just for a few minutes. The more you practice, the more comfortable and confident you will become. Focus on understanding the principles behind each problem rather than just memorizing the steps. This will help you develop a deeper understanding of math and improve your problem-solving skills.
Use Visual Aids
Visual aids can be incredibly helpful for understanding fractions and division. Use diagrams, charts, and manipulatives to visualize the concepts. For example, draw a pie chart to represent fractions or use blocks to represent division. Visual aids can make abstract ideas more concrete and easier to understand.
Break Down Complex Problems
When faced with a complex problem, break it down into smaller, more manageable steps. This will make the problem less daunting and easier to solve. Identify the key elements of the problem and address them one at a time. This approach can help you avoid errors and improve your problem-solving skills.
Check Your Work
Always check your work to ensure accuracy. After solving a problem, review your steps and verify that your answer is correct. Use estimation to check the reasonableness of your answer. If your answer seems too high or too low, review your calculations to find any errors.
Seek Help When Needed
Don't be afraid to ask for help when you're struggling with a concept. Talk to your teacher, a tutor, or a friend who is good at math. There are also many online resources available, such as tutorials, videos, and forums. Seeking help can prevent frustration and help you develop a better understanding of the material.
Connect Math to Real-World Applications
Look for opportunities to connect math to real-world applications. This will help you see the relevance of math to your life and make it more engaging. Use cooking recipes, budgeting scenarios, or measurement problems to practice your skills. Real-world applications can make math more meaningful and memorable.
Understand the Why, Not Just the How
Focus on understanding the reasoning behind mathematical concepts rather than just memorizing procedures. Ask yourself why a particular formula or method works. Understanding the why will help you develop a deeper understanding of math and improve your ability to apply your skills to new and unfamiliar problems.
Use Online Resources
Take advantage of the many online resources available for learning math. Educational websites, math apps, and online calculators can provide you with additional practice and support. Look for resources that offer interactive exercises, step-by-step solutions, and personalized feedback.
Stay Positive
Maintain a positive attitude towards math, even when you're struggling. Math can be challenging, but it's also rewarding. Celebrate your successes and learn from your mistakes. A positive attitude can help you stay motivated and persistent, which are essential for mastering math skills.
FAQ
Q: Why is it important to convert mixed numbers to improper fractions before dividing?
A: Converting mixed numbers to improper fractions simplifies the division process. Improper fractions allow you to perform the division operation more easily by converting it into a multiplication problem using the reciprocal.
Q: What is the reciprocal of a number?
A: The reciprocal of a number is 1 divided by that number. For a fraction, the reciprocal is obtained by swapping the numerator and the denominator. For example, the reciprocal of 2/3 is 3/2.
Q: How do I divide a fraction by a whole number?
A: To divide a fraction by a whole number, you can rewrite the whole number as a fraction with a denominator of 1. Then, multiply the fraction by the reciprocal of the whole number. For example, to divide 1/2 by 2, you would multiply 1/2 by 1/2 (the reciprocal of 2/1), which equals 1/4.
Q: Can I use a calculator to solve "1 and 1/2 divided by 2"?
A: Yes, you can use a calculator to solve this problem. However, it's important to understand the underlying concepts and steps involved. Using a calculator can be a helpful tool for checking your work, but it shouldn't replace your understanding of the math.
Q: What are some real-world applications of dividing fractions?
A: Dividing fractions has numerous real-world applications, such as:
- Cooking: Adjusting recipes to make smaller or larger batches.
- Construction: Calculating dimensions for building projects.
- Finance: Calculating interest rates or dividing expenses.
- Measurement: Converting units of measurement, such as inches to feet or miles to kilometers.
Conclusion
Understanding and accurately calculating "1 and 1/2 divided by 2" is more than just a basic math skill; it's a gateway to grasping more complex mathematical concepts and applying them in everyday situations. By converting mixed numbers to improper fractions, understanding the concept of reciprocals, and practicing regularly, anyone can master this seemingly simple yet fundamental operation.
Now that you have a comprehensive understanding of how to solve "1 and 1/2 divided by 2", put your knowledge to the test! Try solving similar problems and explore other areas of arithmetic to further enhance your skills. Share this article with friends or classmates who might find it helpful, and let's continue to build a stronger foundation in mathematics together. What are some other math topics you'd like to explore? Let us know in the comments below!
Latest Posts
Latest Posts
-
What Is A Shape With 16 Sides Called
Nov 25, 2025
-
Symmetric With Respect To The Y Axis
Nov 25, 2025
-
How Many Acres Are In A Square Mile
Nov 25, 2025
-
Difference Between A Row And Column
Nov 25, 2025
-
How To Calculate Real Gdp Per Capita Growth Rate
Nov 25, 2025
Related Post
Thank you for visiting our website which covers about 1 And 1 2 Divided By 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.