1 4 Divided By 4 As A Fraction
catholicpriest
Nov 10, 2025 · 10 min read
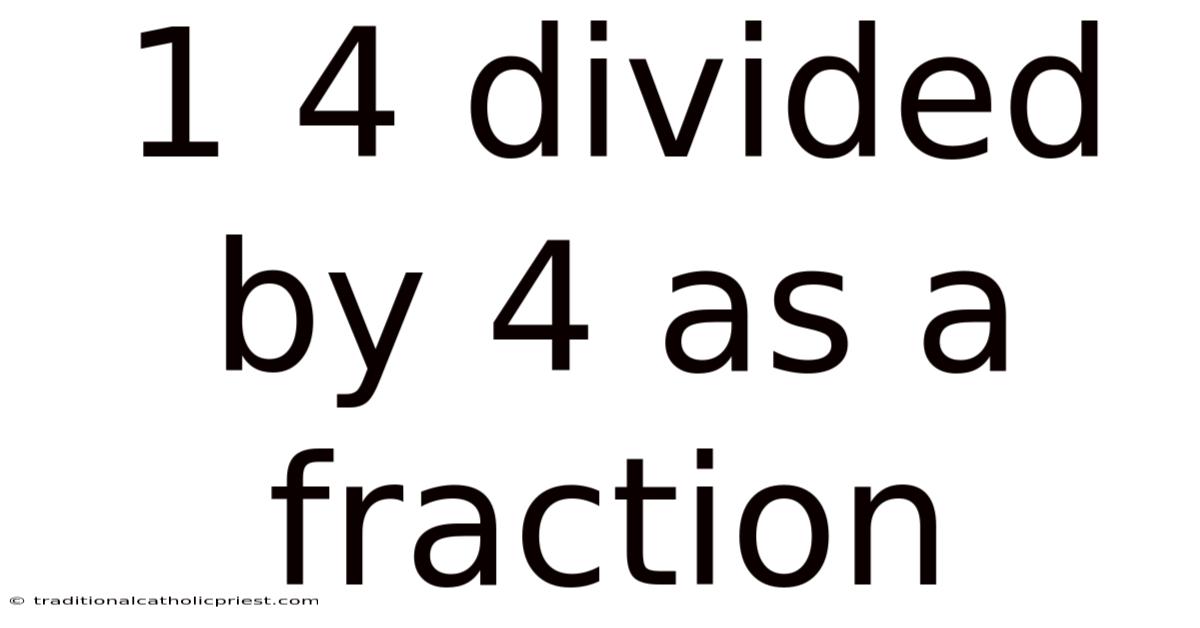
Table of Contents
Imagine you have a single delicious chocolate bar, and you decide to share it with four of your best friends. Each of you gets an equal piece, but how much of the whole bar does each person receive? This simple scenario elegantly introduces the concept of dividing by fractions and expressing the result as a fraction itself. In this case, each friend gets one-fourth (1/4) of the chocolate bar.
The idea of dividing a fraction by a whole number, and then representing the result in fractional form, is a fundamental concept in mathematics. Mastering this skill unlocks more advanced topics and offers practical applications in everyday life. This article will delve into the process of dividing 1/4 by 4, explaining the underlying principles, offering step-by-step instructions, and highlighting real-world examples to make this mathematical operation both clear and accessible.
Understanding the Basics of Dividing Fractions
Dividing fractions can sometimes appear complex, but the core principle is straightforward: dividing by a number is the same as multiplying by its reciprocal. Let's break this down further:
The reciprocal of a number is simply 1 divided by that number. For example, the reciprocal of 2 is 1/2, and the reciprocal of 5 is 1/5. When dealing with fractions, the reciprocal is found by swapping the numerator (the top number) and the denominator (the bottom number). For instance, the reciprocal of 2/3 is 3/2. This swapping action is key to performing division with fractions.
To divide a fraction by a whole number, we convert the whole number into a fraction by placing it over 1. For example, the whole number 4 can be written as the fraction 4/1. Then, we find the reciprocal of this fraction, which is 1/4. Finally, we multiply the original fraction by this reciprocal. This process might seem a bit abstract at first, but with a few examples, it will become second nature.
The concept of reciprocals is deeply rooted in mathematical theory. It's based on the multiplicative inverse property, which states that any number multiplied by its reciprocal equals 1. This property is crucial because multiplying by 1 doesn't change the value of the original number, allowing us to perform division indirectly through multiplication. In essence, when we multiply a fraction by the reciprocal of its divisor, we are finding out how many times the divisor fits into the fraction, just as division intends.
Historically, understanding fractions and their operations has been vital for various applications, from land surveying in ancient Egypt to modern engineering and finance. Fractions allow us to represent parts of a whole and perform accurate calculations, ensuring precise measurements and fair distributions. The ability to divide fractions is particularly important when dealing with ratios, proportions, and scaling problems.
Furthermore, the concept of dividing fractions extends beyond simple numerical calculations. It’s foundational for algebraic manipulations, calculus, and even computer science. For example, in computer graphics, dividing fractions is essential for scaling images and adjusting proportions. In physics, it's used to calculate densities and rates of change. Therefore, mastering this basic operation is crucial for success in many STEM fields.
Step-by-Step Guide: Dividing 1/4 by 4
Now, let's apply these principles to the specific problem of dividing 1/4 by 4. Here's a detailed, step-by-step guide:
Step 1: Write the problem. Start by clearly writing down the division problem: 1/4 ÷ 4
Step 2: Convert the whole number to a fraction. To work with fractions, we need to express the whole number 4 as a fraction. We can do this by placing it over 1: 4 = 4/1 So, our problem now looks like: 1/4 ÷ 4/1
Step 3: Find the reciprocal of the second fraction. The reciprocal of 4/1 is found by swapping the numerator and the denominator: Reciprocal of 4/1 = 1/4
Step 4: Change the division to multiplication. Division is the same as multiplying by the reciprocal, so we change the division sign to a multiplication sign and use the reciprocal we just found: 1/4 ÷ 4/1 becomes 1/4 × 1/4
Step 5: Multiply the fractions. To multiply fractions, we multiply the numerators together and the denominators together: (1 × 1) / (4 × 4)
Step 6: Simplify the result. Perform the multiplication: 1 / 16
Therefore, 1/4 divided by 4 equals 1/16.
This step-by-step method provides a clear and structured approach to dividing fractions by whole numbers. By following these steps, anyone can confidently solve similar problems and gain a deeper understanding of the underlying mathematical principles.
Trends and Latest Developments in Fraction Education
The teaching of fractions has seen significant evolution in recent years, driven by research in mathematics education and advancements in technology. Current trends emphasize a conceptual understanding of fractions rather than rote memorization of rules.
One major trend is the use of visual aids and manipulatives. Tools like fraction bars, pie charts, and number lines help students visualize fractions and understand their relative sizes. These visual representations make abstract concepts more concrete and accessible, especially for younger learners. For instance, using a pie chart to represent 1/4 and then dividing that section into four equal parts can vividly demonstrate that each part represents 1/16 of the whole pie.
Another significant development is the integration of technology in fraction education. Interactive software, educational apps, and online simulations offer engaging ways for students to practice and explore fraction concepts. These digital tools often provide immediate feedback, personalized learning paths, and opportunities for collaborative problem-solving. They can also help students develop a deeper understanding of fractions by allowing them to manipulate virtual objects and experiment with different scenarios.
Furthermore, there is a growing emphasis on real-world applications of fractions. Instead of presenting fractions as abstract mathematical concepts, educators are incorporating practical examples and problem-solving activities that relate to students' lives. For example, cooking recipes, measuring ingredients, and calculating discounts are all excellent contexts for applying fraction skills. This approach helps students see the relevance of fractions and motivates them to learn.
Professional insights from mathematics educators highlight the importance of addressing common misconceptions about fractions. Many students struggle with the idea that fractions represent parts of a whole or that the size of the whole matters when comparing fractions. Addressing these misconceptions requires careful instruction, targeted interventions, and ongoing assessment.
Additionally, there is a growing recognition of the need to differentiate instruction to meet the diverse learning needs of students. Some students may require additional support to master basic fraction concepts, while others may benefit from more challenging activities that extend their understanding. Effective teaching of fractions involves providing individualized instruction, scaffolding learning experiences, and creating opportunities for students to work at their own pace.
Tips and Expert Advice for Mastering Fraction Division
Mastering fraction division requires a combination of understanding the underlying principles, practicing regularly, and applying effective strategies. Here are some tips and expert advice to help you succeed:
1. Focus on Conceptual Understanding: Don't just memorize the rules for dividing fractions. Instead, strive to understand why the rules work. Visualize fractions using diagrams, manipulatives, or real-world examples. This will help you develop a deeper and more intuitive understanding of the concept. For instance, think of dividing a pizza slice (1/4 of a pizza) among friends. If you divide that slice into four equal parts, each friend gets a smaller slice, representing 1/16 of the whole pizza.
2. Practice Regularly: Like any mathematical skill, fraction division requires practice. Work through a variety of problems, starting with simple examples and gradually progressing to more complex ones. Use online resources, textbooks, or worksheets to find practice problems. Consistent practice will help you build confidence and fluency. Try setting aside 15-20 minutes each day to practice fraction problems.
3. Use Visual Aids: Visual aids can be incredibly helpful for understanding fraction division. Draw diagrams, use fraction bars, or create models to represent fractions and their operations. Visualizing fractions can make the abstract concepts more concrete and easier to grasp. For example, draw a rectangle and divide it into four equal parts, representing 1/4. Then, divide each of those parts into four smaller parts. You'll see that the original rectangle is now divided into 16 equal parts, illustrating that 1/4 divided by 4 equals 1/16.
4. Simplify Before Multiplying: When dividing fractions, look for opportunities to simplify before multiplying. This can make the calculations easier and reduce the risk of errors. Simplifying involves canceling out common factors in the numerators and denominators of the fractions. For example, if you are dividing 2/6 by 1/3, you can simplify 2/6 to 1/3 before multiplying by the reciprocal of 1/3 (which is 3/1).
5. Check Your Work: Always check your work to ensure that you have performed the calculations correctly. Use estimation to get a sense of whether your answer is reasonable. For example, if you are dividing 1/4 by 4, you know that the answer should be smaller than 1/4. If you get an answer that is larger than 1/4, you know that you have made a mistake. You can also use a calculator to check your answer, but be sure to understand the underlying principles first.
6. Break Down Complex Problems: If you encounter a complex fraction division problem, break it down into smaller, more manageable steps. Identify the individual operations that need to be performed and tackle them one at a time. This will help you avoid feeling overwhelmed and increase your chances of success. For example, if you have a problem with mixed numbers or multiple operations, convert the mixed numbers to improper fractions and follow the order of operations (PEMDAS).
7. Seek Help When Needed: Don't be afraid to ask for help if you are struggling with fraction division. Talk to your teacher, a tutor, or a classmate. There are also many online resources available, such as video tutorials and interactive exercises. Getting help can clarify confusing concepts and provide you with the support you need to succeed. Many educational websites offer step-by-step solutions and explanations for fraction problems.
FAQ About Dividing Fractions
Q: Why do we flip the second fraction and multiply when dividing fractions? A: Flipping the second fraction and multiplying is equivalent to multiplying by the reciprocal of the fraction. This works because division is the inverse operation of multiplication. Multiplying by the reciprocal effectively "undoes" the division.
Q: Can you divide a fraction by a fraction? A: Yes, you can divide a fraction by another fraction. The process is the same as dividing a fraction by a whole number: find the reciprocal of the second fraction and multiply.
Q: What happens if you divide a fraction by 1? A: Dividing any number (including a fraction) by 1 leaves the number unchanged. So, if you divide 1/4 by 1, the answer is still 1/4.
Q: Is there a shortcut for dividing fractions? A: The "flip and multiply" method is the most efficient way to divide fractions. However, understanding the concept behind it is more important than simply memorizing the shortcut.
Q: How does dividing fractions relate to real-world situations? A: Dividing fractions is used in many real-world situations, such as cooking, measuring, construction, and finance. For example, if you need to divide a recipe in half, you are essentially dividing fractions.
Conclusion
Dividing 1/4 by 4 results in 1/16. This seemingly simple calculation underscores the fundamental principles of fraction division. By understanding the concept of reciprocals and following a step-by-step approach, anyone can confidently tackle similar problems. The ability to divide fractions is not only essential for mathematical proficiency but also valuable in numerous real-world applications.
Now that you have a solid grasp of dividing fractions, practice applying these skills to various problems. Explore online resources, solve practice questions, and challenge yourself with more complex scenarios. Share your newfound knowledge with others and help them understand the beauty and practicality of fractions. Dive deeper into the world of mathematics and discover the endless possibilities that await!
Latest Posts
Latest Posts
-
Whats The Difference Between Cd And Dvd
Nov 10, 2025
-
How Does The Hydronium Ion Form
Nov 10, 2025
-
Compare And Contrast Correlation And Regression
Nov 10, 2025
-
Summary Of The Rocking Horse Winner
Nov 10, 2025
-
What Are The Three Differences Between Rna And Dna
Nov 10, 2025
Related Post
Thank you for visiting our website which covers about 1 4 Divided By 4 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.