1 3 X 2 3 X 1 2
catholicpriest
Nov 13, 2025 · 9 min read
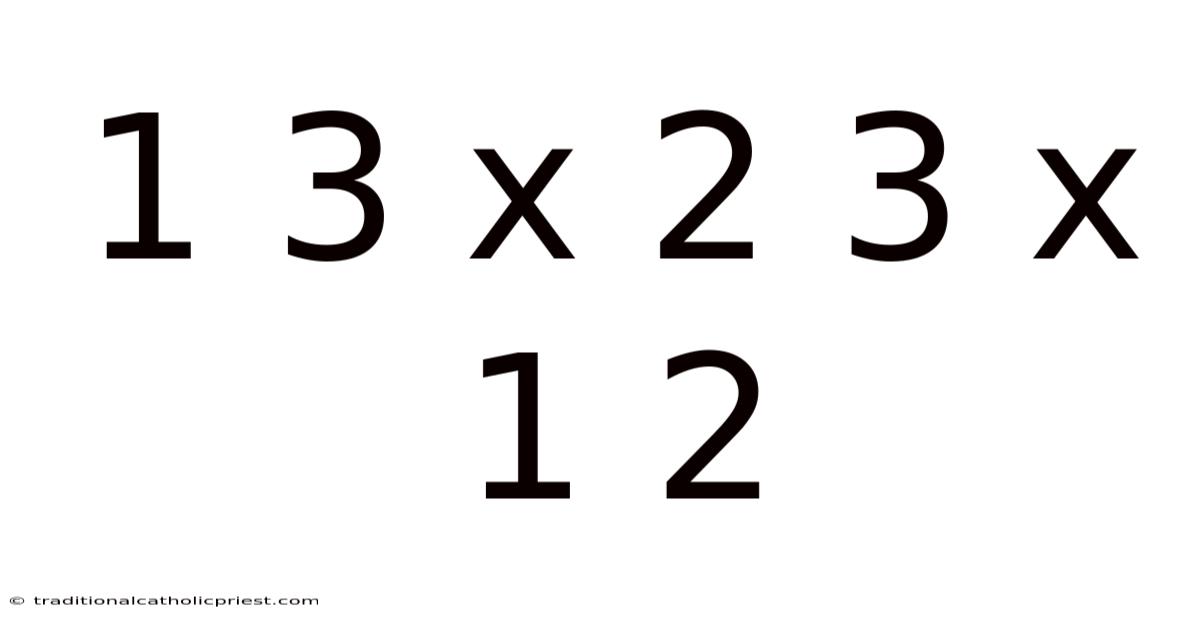
Table of Contents
Imagine trying to describe the size of a room, not in feet or meters, but as a fraction of another room. Or perhaps figuring out how much flour you need for a cake recipe that's been scaled down. These scenarios, while seemingly simple, highlight the importance of understanding fractional arithmetic. At its core, 1/3 x 2/3 x 1/2 is a mathematical expression involving the multiplication of fractions. While it looks straightforward, mastering the concept behind it is crucial for more complex calculations and real-world problem-solving.
The expression 1/3 x 2/3 x 1/2 represents a fundamental operation in mathematics: the multiplication of fractions. This seemingly simple arithmetic problem opens the door to a wide range of applications, from everyday calculations to complex scientific computations. Understanding how to accurately perform and interpret this operation is essential for anyone looking to build a solid foundation in mathematics. This article will delve into the intricacies of this calculation, providing a comprehensive overview, real-world examples, and expert tips to ensure a thorough understanding.
Main Subheading
The multiplication of fractions is a core concept in arithmetic, serving as a building block for more advanced mathematical operations. Fractions, by definition, represent parts of a whole. When we multiply them, we are essentially finding a fraction of another fraction. The expression 1/3 x 2/3 x 1/2, therefore, asks us to find one-third of two-thirds of one-half.
To truly appreciate the process and its implications, it is crucial to understand the basic principles that govern fractional arithmetic. This includes not only the mechanical steps involved in multiplying fractions but also the conceptual understanding of what these operations represent. From visualizing fractions as portions of a pie to applying them in practical situations like cooking or measuring, a solid grasp of the basics will significantly enhance your ability to work with fractions effectively.
Comprehensive Overview
Definition of Fractions
A fraction represents a part of a whole or, more generally, any number of equal parts. It is written as a/b, where a is the numerator (the number of parts we have) and b is the denominator (the total number of parts that make up the whole). For instance, 1/2 means one part out of two equal parts, and 2/3 means two parts out of three equal parts.
Principles of Fraction Multiplication
The multiplication of fractions is straightforward: you multiply the numerators together to get the new numerator, and you multiply the denominators together to get the new denominator. Mathematically, this is expressed as: (a/b) * (c/d) = (ac) / (bd).
This principle extends to multiplying any number of fractions. In the case of 1/3 x 2/3 x 1/2, we apply the same rule sequentially:
- Multiply 1/3 by 2/3: (1 * 2) / (3 * 3) = 2/9
- Multiply the result (2/9) by 1/2: (2 * 1) / (9 * 2) = 2/18
Simplifying Fractions
After performing the multiplication, it is often necessary to simplify the resulting fraction to its lowest terms. Simplifying a fraction means dividing both the numerator and the denominator by their greatest common divisor (GCD). In our example, the fraction 2/18 can be simplified because both 2 and 18 are divisible by 2. Dividing both the numerator and the denominator by 2 gives us 1/9.
Historical Context
The concept of fractions dates back to ancient civilizations, with evidence of their use found in Egyptian and Mesopotamian texts. Egyptians used fractions extensively in measurement and land division, while Mesopotamians developed a sophisticated system of sexagesimal (base-60) fractions. The modern notation of fractions, with a horizontal line separating the numerator and denominator, was popularized by Arab mathematicians during the medieval period. Over time, fractions became an integral part of mathematics, crucial for trade, engineering, and scientific advancements.
Visual Representation
Visualizing fractions can greatly aid in understanding their multiplication. Consider a rectangle divided into three equal parts, representing 1/3. Now, take two of these parts, representing 2/3. Finally, consider half of the 2/3. What you are left with is 1/9 of the original rectangle. This visual representation helps to solidify the concept that multiplying fractions is about finding a part of a part. Another way to visualize this is by using pie charts or number lines, both of which offer intuitive ways to represent fractions and their operations.
Trends and Latest Developments
Digital Tools and Education
With the advent of technology, various digital tools and educational platforms have emerged to facilitate the understanding and application of fractions. Interactive simulations, online calculators, and educational apps provide students with hands-on experience in manipulating fractions and solving related problems. These resources often include visual aids and real-time feedback, making learning more engaging and effective.
Real-World Applications in Data Analysis
In today's data-driven world, fractions play a crucial role in data analysis and statistics. Proportions, percentages, and ratios, all of which are based on fractions, are used to interpret data, make predictions, and inform decision-making. For example, analysts might use fractions to represent market share, calculate risk probabilities, or analyze survey results. A solid understanding of fractional arithmetic is therefore essential for professionals in these fields.
Incorporating Fractions in AI and Machine Learning
Even in advanced fields like artificial intelligence (AI) and machine learning, fractions have their place. For example, probabilities in machine learning models are often represented as fractions or decimals derived from fractions. Feature scaling techniques, which are used to normalize data for machine learning algorithms, also rely on fractional arithmetic. As AI continues to evolve, the importance of understanding these fundamental concepts will only grow.
Current Educational Reforms
Educational reforms around the globe are increasingly focusing on developing a deeper conceptual understanding of mathematics, rather than rote memorization of procedures. This includes emphasizing the importance of fractions as a foundation for algebra and calculus. Educators are employing innovative teaching methods, such as hands-on activities and real-world problem-solving, to help students grasp the underlying principles of fractional arithmetic and its applications.
The Role of Fractions in Quantum Physics
While it may seem far-fetched, fractions even play a role in quantum physics. Certain quantum phenomena are described using fractional quantum numbers, which are fractions that represent the properties of particles. These concepts, although highly advanced, underscore the pervasive nature of fractions in both theoretical and applied sciences.
Tips and Expert Advice
Start with Visualization
One of the most effective ways to understand fractions is through visualization. Use diagrams, pie charts, or even physical objects to represent fractions and their operations. This helps to make the abstract concept more concrete and easier to grasp. For example, when teaching 1/3 x 2/3 x 1/2, start by drawing a rectangle and dividing it into three equal parts. Shade one of these parts to represent 1/3. Then, divide the entire rectangle into thirds again horizontally, shading two of those sections to represent 2/3. Finally, split the whole rectangle in half and consider only half of the already shaded area. You will see that the final shaded area represents 1/9 of the original rectangle.
Practice Regularly
Like any mathematical skill, proficiency in fractional arithmetic requires regular practice. Work through a variety of problems, starting with simple examples and gradually progressing to more complex ones. Use online resources, textbooks, or worksheets to find practice problems. Consistency is key to building confidence and accuracy.
Relate Fractions to Real-World Situations
Connecting fractions to real-world scenarios can make learning more relevant and engaging. For example, use fractions to calculate cooking measurements, determine proportions in a recipe, or figure out discounts at a store. By seeing how fractions are used in everyday life, you can develop a deeper appreciation for their importance and practical applications.
Master Simplification Techniques
Simplifying fractions is a crucial skill that can save time and reduce errors. Learn how to find the greatest common divisor (GCD) of the numerator and denominator, and practice simplifying fractions to their lowest terms. This will not only make your calculations easier but also improve your understanding of the relationships between different fractions.
Understand the Concept of "Of" in Multiplication
When multiplying fractions, remember that the word "of" often implies multiplication. For example, "1/2 of 1/4" means 1/2 multiplied by 1/4. Recognizing this connection can help you translate real-world problems into mathematical expressions involving fractions.
FAQ
Q: What does 1/3 x 2/3 x 1/2 mean? A: It means finding one-third of two-thirds of one-half. Mathematically, it involves multiplying these three fractions together.
Q: How do you multiply fractions? A: Multiply the numerators together to get the new numerator, and multiply the denominators together to get the new denominator.
Q: What is the result of 1/3 x 2/3 x 1/2? A: The result is 1/9. (1/3) * (2/3) * (1/2) = 2/18, which simplifies to 1/9.
Q: Why is it important to simplify fractions? A: Simplifying fractions makes them easier to understand and compare. It also helps in avoiding confusion when dealing with larger numbers.
Q: Can you use a calculator to multiply fractions? A: Yes, most calculators have fraction functions that can simplify the process. However, understanding the underlying principles is still essential.
Q: Are fractions used in real life? A: Absolutely. Fractions are used in cooking, measurements, finance, and many other practical applications.
Q: What if I need to multiply mixed numbers (e.g., 1 1/2 x 2/3)? A: First, convert the mixed number to an improper fraction. For example, 1 1/2 becomes 3/2. Then, multiply as usual.
Q: How do I find the greatest common divisor (GCD) to simplify fractions? A: You can use methods like prime factorization or the Euclidean algorithm to find the GCD. Online calculators are also available for this purpose.
Q: What's the difference between a proper and an improper fraction? A: A proper fraction has a numerator smaller than the denominator (e.g., 2/3), while an improper fraction has a numerator greater than or equal to the denominator (e.g., 5/2).
Q: How do I divide fractions? A: To divide fractions, you multiply by the reciprocal of the second fraction. For example, (1/2) ÷ (1/4) = (1/2) * (4/1) = 2.
Conclusion
In summary, 1/3 x 2/3 x 1/2 is a simple yet fundamental arithmetic problem that highlights the importance of understanding fraction multiplication. By grasping the basic principles, visualizing the operations, and practicing regularly, anyone can master this skill and apply it to various real-world scenarios. From data analysis and cooking to advanced scientific applications, fractions are an indispensable tool for problem-solving and critical thinking.
Now that you have a comprehensive understanding of multiplying fractions, take the next step by practicing with more complex problems and exploring real-world applications. Share this article with others who might benefit from it and leave a comment below with your own experiences or questions about fractions. Let's continue to build our mathematical knowledge together!
Latest Posts
Latest Posts
-
What Is 2 Pi R Squared
Nov 13, 2025
-
An Atom Is Electrically Neutral Because
Nov 13, 2025
-
What Is The Function Of The Bacterial Cell Wall
Nov 13, 2025
-
Words With 4 Letters Starting With S
Nov 13, 2025
-
2 Miles Equals How Many Feet
Nov 13, 2025
Related Post
Thank you for visiting our website which covers about 1 3 X 2 3 X 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.