1/3 X 1/3 X 1/3 X 1/3
catholicpriest
Nov 14, 2025 · 10 min read
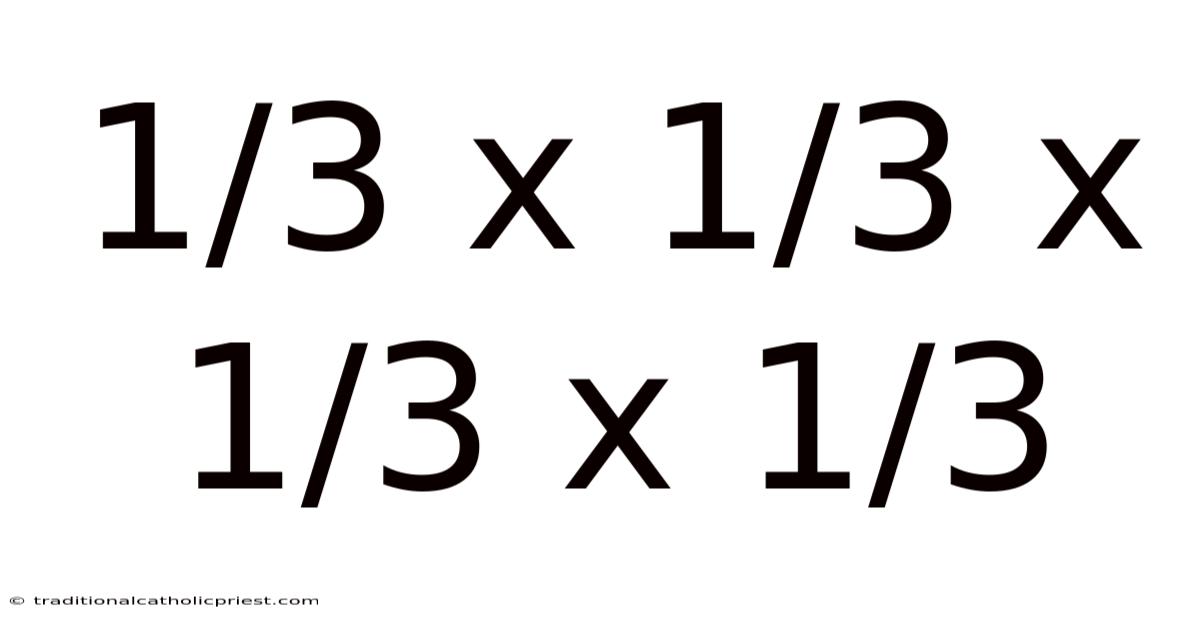
Table of Contents
Imagine dividing a cake into three equal slices. Now, imagine taking one of those slices and dividing it into three again. If you repeat this process two more times, how much of the original cake do you have? This might sound like a simple math problem, but it beautifully illustrates the concept behind multiplying fractions, a fundamental skill that unlocks a world of mathematical possibilities.
The problem "1/3 x 1/3 x 1/3 x 1/3" may appear straightforward, but it acts as a gateway to understanding exponents, fractional arithmetic, and even more complex mathematical ideas. This article will delve deep into the world of fraction multiplication, exploring its basic principles, real-world applications, and practical tips to master this essential skill. Whether you are a student looking to improve your math skills or simply curious about the intricacies of fractions, this comprehensive guide will provide you with a solid understanding of multiplying fractions, particularly when the same fraction is multiplied multiple times.
Understanding the Basics of Fraction Multiplication
At its core, multiplying fractions involves combining parts of a whole. When you multiply 1/3 by 1/3, you are essentially taking one-third of one-third. The beauty of fraction multiplication lies in its simplicity: you multiply the numerators (the top numbers) together and the denominators (the bottom numbers) together. This process provides a clear and straightforward method for determining the resulting fraction.
Mathematically, the rule for multiplying fractions can be expressed as: (a/b) * (c/d) = (ac) / (bd). This formula states that when you multiply two fractions, a/b and c/d, the result is a new fraction where the numerator is the product of the original numerators (a and c) and the denominator is the product of the original denominators (b and d). This rule applies regardless of the type of fractions involved, whether they are proper fractions (numerator less than the denominator), improper fractions (numerator greater than or equal to the denominator), or mixed numbers (a whole number and a fraction). Understanding and applying this basic rule is the first step in mastering fraction multiplication.
Fractions are written with a numerator (the top number) and a denominator (the bottom number), separated by a horizontal line. The numerator represents the number of parts you have, while the denominator represents the total number of equal parts the whole is divided into. For example, in the fraction 1/3, "1" is the numerator, indicating that you have one part, and "3" is the denominator, indicating that the whole is divided into three equal parts. In essence, a fraction represents a part-to-whole relationship.
The concept of fractions dates back to ancient civilizations, with evidence of their use found in ancient Egypt and Mesopotamia. Egyptians used fractions to solve practical problems related to land measurement, construction, and trade. They primarily worked with unit fractions (fractions with a numerator of 1), such as 1/2, 1/3, and 1/4. Mesopotamians, on the other hand, developed a more sophisticated system of fractions based on the number 60, which is still reflected in our measurement of time (60 seconds in a minute, 60 minutes in an hour) and angles (360 degrees in a circle). The development of fractions was crucial for advancing mathematics and its applications in various fields.
Multiplying the same fraction multiple times, as in the case of 1/3 x 1/3 x 1/3 x 1/3, introduces the concept of exponents. An exponent indicates how many times a number (the base) is multiplied by itself. In this example, we are multiplying 1/3 by itself four times, which can be written as (1/3)^4. This notation simplifies the representation of repeated multiplication and makes it easier to perform calculations. Understanding exponents is essential for simplifying complex expressions and solving more advanced mathematical problems.
Fraction multiplication has numerous practical applications in everyday life. From cooking and baking to measuring ingredients and calculating proportions, fractions are indispensable. For example, if a recipe calls for 1/2 cup of flour and you want to make half the recipe, you would need to multiply 1/2 by 1/2 to determine the new amount of flour needed (1/4 cup). In construction, fractions are used to measure lengths, calculate areas, and determine the quantities of materials needed for a project. In finance, fractions are used to calculate interest rates, discounts, and investment returns. The ability to work with fractions is a valuable skill that enhances problem-solving abilities and decision-making in various real-world scenarios.
Trends and Latest Developments
In recent years, there has been a renewed emphasis on improving math education, particularly in the area of fractions. Educational research has highlighted the importance of developing a strong conceptual understanding of fractions, rather than simply memorizing procedures. This approach involves using visual aids, manipulatives, and real-world examples to help students grasp the underlying principles of fractions. For example, using fraction bars or pie charts can help students visualize the relationship between the numerator and the denominator and understand how fractions are added, subtracted, multiplied, and divided.
Technology has also played a significant role in enhancing fraction education. Interactive apps, online games, and educational software provide students with engaging and personalized learning experiences. These tools often include features such as step-by-step tutorials, practice exercises with immediate feedback, and virtual manipulatives that allow students to explore fractions in a dynamic and interactive way. Adaptive learning platforms can also tailor the difficulty level of the exercises to each student's individual needs, ensuring that they are challenged appropriately and receive targeted support where they need it most.
There is a growing consensus among educators that fractions should be taught in a way that connects to students' real-life experiences. This involves incorporating real-world problems and scenarios into the curriculum, such as cooking, shopping, and sports. By seeing how fractions are used in everyday contexts, students are more likely to develop a deeper understanding of their relevance and importance. For example, a lesson on fractions could involve calculating the cost of items on sale, determining the batting averages of baseball players, or measuring ingredients for a recipe. This approach not only makes learning more engaging but also helps students develop critical thinking and problem-solving skills.
Another trend in fraction education is the use of collaborative learning activities. Working in groups allows students to share their ideas, discuss different approaches to solving problems, and learn from each other. Collaborative activities can also help students develop communication and teamwork skills, which are essential for success in both academic and professional settings. For example, a group activity could involve solving a complex word problem that requires students to apply their knowledge of fractions, decimals, and percentages. By working together, students can learn to appreciate different perspectives and develop a deeper understanding of the concepts involved.
Despite these advancements, there are still challenges in fraction education. Many students struggle with fractions due to a lack of conceptual understanding and a reliance on rote memorization. This can lead to difficulties in more advanced math courses, such as algebra and calculus. To address these challenges, educators need to focus on developing a strong foundation in fractions from an early age, using effective teaching strategies and incorporating technology and real-world examples into the curriculum. By doing so, we can help students develop the skills and confidence they need to succeed in mathematics and beyond.
Tips and Expert Advice
When multiplying the same fraction multiple times, like 1/3 x 1/3 x 1/3 x 1/3, simplify the process by recognizing it as an exponent. As mentioned before, (1/3) x (1/3) x (1/3) x (1/3) can be written as (1/3)^4. This allows you to calculate the numerator and the denominator separately. The numerator is 1^4, which equals 1, and the denominator is 3^4, which equals 81. Therefore, (1/3)^4 equals 1/81.
Before multiplying fractions, always check if you can simplify them first. Simplifying fractions involves dividing both the numerator and the denominator by their greatest common factor (GCF). For example, if you were multiplying 2/4 by 3/6, you could simplify 2/4 to 1/2 and 3/6 to 1/2 before multiplying. This would make the multiplication easier: (1/2) * (1/2) = 1/4. Simplifying fractions before multiplying can save you time and reduce the risk of making errors.
Visual aids can be incredibly helpful when learning fraction multiplication. Use diagrams, such as fraction bars or pie charts, to represent the fractions and visualize the multiplication process. For example, to multiply 1/2 by 1/3, you can draw a rectangle and divide it into three equal parts, representing 1/3. Then, shade one of those parts. Next, divide the rectangle in half horizontally, representing 1/2. The area that is both shaded and horizontally divided represents the product of 1/2 and 1/3, which is 1/6.
Practice regularly to reinforce your understanding of fraction multiplication. Start with simple problems and gradually increase the difficulty level. Use online resources, textbooks, or worksheets to find practice problems. The more you practice, the more comfortable and confident you will become with fraction multiplication. Consider using flashcards to memorize common fraction multiplications, such as 1/2 * 1/2, 1/3 * 1/3, and 1/4 * 1/4.
Understand the relationship between fractions and decimals. Fractions and decimals are two different ways of representing the same numbers. For example, 1/2 is equal to 0.5, 1/4 is equal to 0.25, and 1/3 is equal to approximately 0.333. Knowing these equivalents can help you convert fractions to decimals and vice versa, which can be useful in certain situations. For example, if you are multiplying a fraction by a decimal, you can convert the fraction to a decimal or the decimal to a fraction to make the calculation easier.
FAQ
Q: What is a fraction? A: A fraction represents a part of a whole. It is written as a numerator (the top number) over a denominator (the bottom number), separated by a horizontal line. The numerator indicates the number of parts you have, while the denominator indicates the total number of equal parts the whole is divided into.
Q: How do you multiply fractions? A: To multiply fractions, multiply the numerators together to get the new numerator and multiply the denominators together to get the new denominator. The formula is (a/b) * (c/d) = (ac) / (bd).
Q: What does it mean to simplify a fraction? A: Simplifying a fraction means reducing it to its simplest form by dividing both the numerator and the denominator by their greatest common factor (GCF).
Q: How can visual aids help in understanding fraction multiplication? A: Visual aids such as fraction bars and pie charts can help you visualize the fractions and the multiplication process, making it easier to understand how the parts combine.
Q: What is the relationship between fractions and exponents? A: Multiplying the same fraction multiple times can be represented using exponents. For example, (1/3) x (1/3) x (1/3) x (1/3) can be written as (1/3)^4.
Conclusion
Mastering the multiplication of fractions, especially repeated multiplication like 1/3 x 1/3 x 1/3 x 1/3, is a crucial step in building a strong foundation in mathematics. Understanding the basic principles, simplifying fractions, using visual aids, and practicing regularly are key to success. By recognizing the connection to exponents and exploring real-world applications, you can deepen your understanding and appreciation of fractions.
Now that you have a solid grasp of multiplying fractions, take the next step and apply your knowledge to solve real-world problems. Practice with different types of fractions and explore more advanced concepts, such as dividing fractions and working with mixed numbers. Share this article with friends or classmates who might also benefit from understanding fractions better. Leave a comment below with any questions or insights you have about multiplying fractions. Your engagement will help create a collaborative learning environment and inspire others to explore the fascinating world of mathematics.
Latest Posts
Latest Posts
-
Bacterial Flagella Can Move In Directions
Nov 14, 2025
-
The Cathode Ray Tube Experiment Determined
Nov 14, 2025
-
How To Convert A Decimal To Percentage
Nov 14, 2025
-
How Many Rows Are In Excel
Nov 14, 2025
-
Can You Have A Pet Flying Squirrel
Nov 14, 2025
Related Post
Thank you for visiting our website which covers about 1/3 X 1/3 X 1/3 X 1/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.