1 1 2 Divided By 1 4 As A Fraction
catholicpriest
Nov 08, 2025 · 13 min read
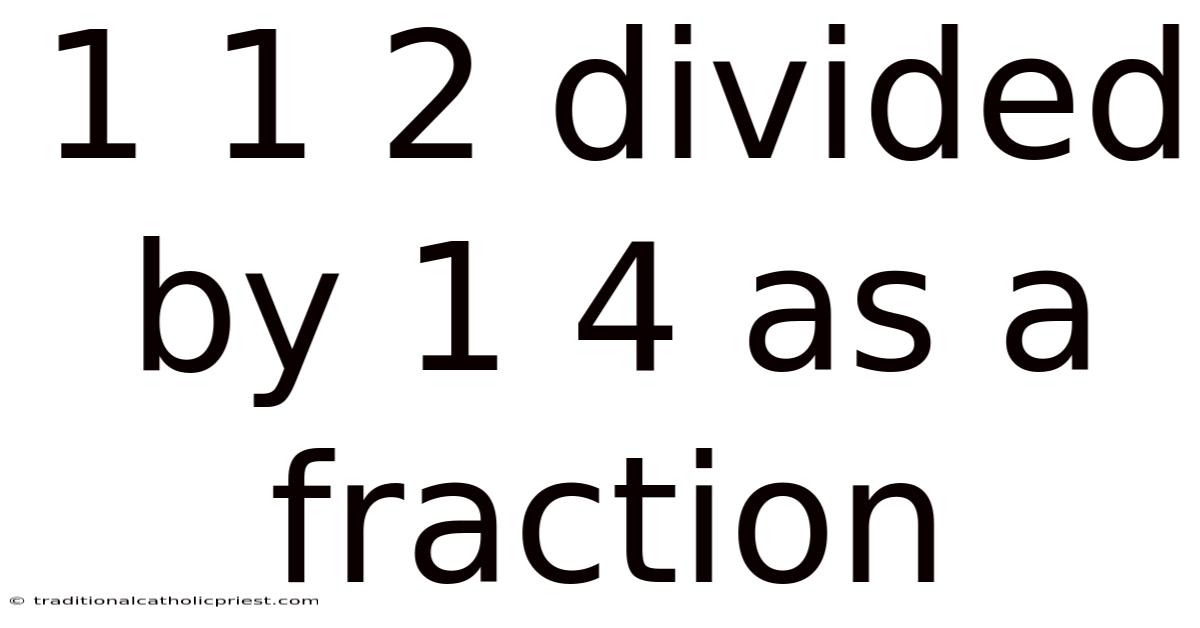
Table of Contents
Imagine you are baking a cake and the recipe calls for 1 1/2 cups of flour, but you only have a 1/4 cup measuring scoop. How many scoops do you need? This is a real-life scenario where understanding how to divide fractions becomes incredibly useful. Fractions are not just abstract numbers; they are part of our everyday experiences, from cooking and baking to measuring distances and sharing resources.
Many people find fractions daunting, especially when it comes to division. The simple act of dividing 1 1/2 by 1/4 can seem confusing if you don't know the steps involved. But fear not! This guide will break down the process in a clear, easy-to-understand manner, transforming what might seem like a complex problem into a straightforward calculation. By the end of this article, you'll not only know how to divide 1 1/2 by 1/4 as a fraction but also understand the underlying principles that make it all work.
Dividing 1 1/2 by 1/4 as a Fraction
To divide 1 1/2 by 1/4 as a fraction, we need to understand the basic principles of fraction division. Fraction division might seem tricky at first, but it becomes much simpler when you break it down into manageable steps. The key is to remember that dividing by a fraction is the same as multiplying by its reciprocal. This simple trick transforms division problems into multiplication problems, which are often easier to handle.
Before diving into the specific calculation, let’s ensure we understand the fundamental concepts. Fractions represent parts of a whole, with the numerator (the top number) indicating how many parts we have and the denominator (the bottom number) indicating the total number of parts the whole is divided into. When dividing fractions, we are essentially asking how many times one fraction fits into another. The concept of reciprocals is also crucial. The reciprocal of a fraction is obtained by swapping its numerator and denominator. For example, the reciprocal of 1/4 is 4/1. Understanding these basics will make the process of dividing 1 1/2 by 1/4 much clearer and more intuitive.
Comprehensive Overview
What are Fractions?
Fractions are a fundamental part of mathematics used to represent portions of a whole. They consist of two parts: the numerator and the denominator. The numerator indicates the number of parts being considered, while the denominator indicates the total number of equal parts that make up the whole. For example, in the fraction 3/4, the numerator is 3, and the denominator is 4. This means we are considering 3 parts out of a total of 4 equal parts.
Fractions can be classified into several types:
- Proper Fractions: These are fractions where the numerator is less than the denominator, such as 1/2, 3/4, and 2/5. Proper fractions represent values less than one.
- Improper Fractions: These are fractions where the numerator is greater than or equal to the denominator, such as 5/3, 7/4, and 3/3. Improper fractions represent values greater than or equal to one.
- Mixed Numbers: These consist of a whole number and a proper fraction, such as 1 1/2, 2 3/4, and 5 1/5. Mixed numbers are another way to represent values greater than one.
The Concept of Division with Fractions
Dividing fractions involves determining how many times one fraction (the divisor) fits into another fraction (the dividend). This concept can be visualized using real-world examples. For instance, if you have a pizza cut into 1/2 slices and you want to divide it among people, each getting 1/8 of the pizza, you are essentially dividing 1/2 by 1/8 to find out how many people can be served.
The standard method for dividing fractions involves multiplying the dividend by the reciprocal of the divisor. The reciprocal of a fraction is obtained by swapping its numerator and denominator. This method works because dividing by a number is the same as multiplying by its inverse. In the case of fractions, the reciprocal serves as the multiplicative inverse.
Reciprocals and Why They Matter
The reciprocal of a fraction is a key concept in division. To find the reciprocal of a fraction, you simply swap the numerator and the denominator. For example:
- The reciprocal of 2/3 is 3/2.
- The reciprocal of 1/4 is 4/1 (or simply 4).
- The reciprocal of 5/2 is 2/5.
The reason reciprocals are important is that dividing by a fraction is mathematically equivalent to multiplying by its reciprocal. This transformation simplifies the division process, allowing us to perform multiplication instead, which is often easier to compute.
Step-by-Step Calculation: 1 1/2 Divided by 1/4
Now, let's apply these concepts to the specific problem of dividing 1 1/2 by 1/4.
-
Convert the mixed number to an improper fraction:
- 1 1/2 can be converted to an improper fraction by multiplying the whole number (1) by the denominator (2) and adding the numerator (1). This gives us (1 * 2) + 1 = 3. So, 1 1/2 is equivalent to 3/2.
-
Identify the divisor and find its reciprocal:
- We are dividing 3/2 by 1/4. The divisor is 1/4.
- The reciprocal of 1/4 is 4/1 (or simply 4).
-
Multiply the dividend by the reciprocal of the divisor:
-
Now, we multiply 3/2 by 4/1:
- (3/2) * (4/1) = (3 * 4) / (2 * 1) = 12/2
-
-
Simplify the resulting fraction:
-
The fraction 12/2 can be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is 2:
- 12/2 = 6/1 = 6
-
Therefore, 1 1/2 divided by 1/4 equals 6.
Real-World Applications
Understanding how to divide fractions is not just an academic exercise; it has numerous practical applications in everyday life. Here are a few examples:
- Cooking and Baking: Recipes often involve fractions. If you need to scale a recipe up or down, you'll need to divide or multiply fractions. For example, if a recipe calls for 1/2 cup of sugar and you want to make half the recipe, you need to divide 1/2 by 2, resulting in 1/4 cup.
- Construction and Carpentry: Measuring lengths and cutting materials often involve fractions. For example, if you need to cut a board that is 3 1/2 feet long into sections that are 1/4 foot each, you would divide 3 1/2 by 1/4 to determine how many sections you can get.
- Time Management: Dividing tasks or time slots can involve fractions. For example, if you have 1 1/2 hours to complete three tasks, you might divide 1 1/2 by 3 to determine how much time you can allocate to each task.
- Sharing Resources: Dividing resources equally among a group of people often involves fractions. For example, if you have 2 1/4 pizzas to share among 6 people, you would divide 2 1/4 by 6 to determine how much pizza each person gets.
Trends and Latest Developments
While the basic principles of fraction division remain constant, there are some trends and developments in how fractions are taught and used, particularly with the integration of technology.
Visual and Interactive Learning Tools
One significant trend is the use of visual and interactive learning tools to help students understand fractions. These tools include:
- Fraction Bars and Circles: These physical and digital manipulatives allow students to visually represent fractions and perform operations like division.
- Online Simulations: Interactive simulations allow students to experiment with fractions and division in a dynamic and engaging way.
- Educational Games: Games that incorporate fraction division can make learning more enjoyable and effective.
These tools help students develop a deeper understanding of fractions by connecting abstract concepts to concrete representations.
Emphasis on Conceptual Understanding
Traditional math education often focuses on rote memorization of rules and procedures. However, there is a growing emphasis on conceptual understanding in modern math education. This means that students are encouraged to understand why mathematical rules work, rather than simply memorizing them.
For example, when teaching fraction division, educators now focus on explaining why dividing by a fraction is the same as multiplying by its reciprocal, rather than just telling students to "flip and multiply." This approach helps students develop a more robust and flexible understanding of fractions.
Integration with Technology
Technology plays an increasingly important role in math education. Software and apps can provide personalized learning experiences and immediate feedback, helping students master fraction division at their own pace.
- Adaptive Learning Platforms: These platforms adjust the difficulty of problems based on a student's performance, providing customized instruction.
- Online Calculators: While not a replacement for understanding the concepts, online calculators can be useful for checking answers and performing complex calculations.
- Video Tutorials: Online video tutorials can provide step-by-step explanations of fraction division, allowing students to learn at their own pace.
Current Data and Research
Recent research in math education highlights the importance of early intervention and targeted instruction for students struggling with fractions. Studies have shown that students who develop a strong understanding of fractions in elementary school are more likely to succeed in higher-level math courses.
Additionally, data from standardized tests indicate that fraction concepts remain a challenging area for many students. This underscores the need for effective teaching strategies and ongoing support to help students master fractions.
Tips and Expert Advice
Here are some practical tips and expert advice to help you master dividing 1 1/2 by 1/4 and other fraction division problems:
1. Master the Basics
Before tackling complex fraction division problems, make sure you have a solid understanding of the basics. This includes:
- Understanding Fractions: Know the definition of fractions, the different types of fractions (proper, improper, mixed), and how to represent them visually.
- Converting Mixed Numbers: Be able to convert mixed numbers to improper fractions and vice versa. This is essential for performing calculations with mixed numbers.
- Simplifying Fractions: Know how to simplify fractions by dividing both the numerator and denominator by their greatest common divisor.
A strong foundation in these basics will make fraction division much easier.
2. Visualize the Problem
Visualizing the problem can help you understand what you are trying to do. For example, when dividing 1 1/2 by 1/4, you can imagine having 1 1/2 pizzas and wanting to divide them into slices that are 1/4 of a pizza each. How many slices would you have?
You can use diagrams, drawings, or physical manipulatives to help you visualize the problem. This can make the abstract concept of fraction division more concrete and easier to grasp.
3. Practice Regularly
Like any skill, mastering fraction division requires practice. Set aside time each day or week to work on fraction problems. Start with simple problems and gradually work your way up to more complex ones.
Use a variety of resources, such as textbooks, worksheets, and online practice sites, to get plenty of practice. The more you practice, the more confident and proficient you will become.
4. Use Real-World Examples
Connect fraction division to real-world situations. This can make the concept more relevant and meaningful. For example, think about dividing recipes, measuring ingredients, or sharing resources.
By seeing how fractions are used in everyday life, you will develop a deeper understanding of their importance and how to work with them.
5. Check Your Work
Always check your work to make sure you have arrived at the correct answer. You can do this by:
- Estimating: Estimate the answer before you start working on the problem. This can help you catch errors if your final answer is way off.
- Using a Calculator: Use a calculator to check your answer. However, be sure to understand the steps involved in fraction division, rather than just relying on the calculator.
- Working Backwards: Multiply your answer by the divisor to see if you get the dividend. For example, if you find that 1 1/2 divided by 1/4 equals 6, check that 6 * (1/4) = 1 1/2.
6. Understand the "Why"
Don't just memorize the rules for fraction division. Take the time to understand why those rules work. For example, understand why dividing by a fraction is the same as multiplying by its reciprocal.
This deeper understanding will make you more flexible and adaptable in solving fraction problems. You will also be better able to apply your knowledge to new and unfamiliar situations.
7. Seek Help When Needed
Don't be afraid to ask for help if you are struggling with fraction division. Talk to your teacher, a tutor, or a friend who is good at math. There are also many online resources available, such as video tutorials and forums, where you can get help with specific problems.
Remember, everyone learns at their own pace. Don't get discouraged if you don't understand something right away. Keep practicing and seeking help when needed, and you will eventually master fraction division.
FAQ
Q: Why do we flip the second fraction when dividing?
A: Flipping the second fraction (the divisor) and multiplying is the same as multiplying by the reciprocal. This works because division is the inverse operation of multiplication. By multiplying by the reciprocal, you are effectively undoing the division.
Q: Can I use a calculator for fraction division?
A: Yes, you can use a calculator to check your work or perform complex calculations. However, it's important to understand the steps involved in fraction division, rather than just relying on the calculator. Calculators are tools, not replacements for understanding.
Q: What if I have a negative fraction?
A: The same rules apply for dividing negative fractions. Remember that dividing a negative number by a positive number (or vice versa) results in a negative answer. If both fractions are negative, the result is positive.
Q: How do I divide mixed numbers?
A: First, convert the mixed numbers to improper fractions. Then, follow the same steps as with regular fractions: flip the second fraction (the divisor) and multiply.
Q: Is there another way to think about fraction division?
A: Yes, you can think of fraction division as asking "How many times does this fraction fit into that fraction?" For example, when dividing 1/2 by 1/4, you are asking how many 1/4s are in 1/2.
Conclusion
Dividing 1 1/2 by 1/4 as a fraction involves converting the mixed number to an improper fraction, finding the reciprocal of the divisor, and then multiplying. This process transforms a division problem into a multiplication problem, which is often easier to solve. The result of dividing 1 1/2 by 1/4 is 6, illustrating how many 1/4 units fit into 1 1/2 units.
Understanding fraction division is not just a mathematical exercise; it's a practical skill with applications in cooking, construction, time management, and resource sharing. By mastering the basics, visualizing problems, practicing regularly, and seeking help when needed, anyone can become proficient in dividing fractions.
Ready to put your knowledge to the test? Try solving similar problems and explore more advanced fraction operations. Share your solutions or ask any further questions in the comments below! Your engagement will help solidify your understanding and help others learn as well.
Latest Posts
Latest Posts
-
How Do You Say 79 In French
Nov 08, 2025
-
Why Do They Call It Horsepower
Nov 08, 2025
-
Clustered Index Versus Non Clustered Index
Nov 08, 2025
-
What Is A Bunch Of Penguins Called
Nov 08, 2025
-
Diagram Of The Human Foot Bones
Nov 08, 2025
Related Post
Thank you for visiting our website which covers about 1 1 2 Divided By 1 4 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.